
ベクトル
ベクトルとは、「大きさと向き」を持つ量のことをいいます。
ベクトルは、矢印を使って表すことができるできます。例えば、風、重力、速度、力、電気、磁気などのありとあらゆる物体の運動を理解するうえでベクトルの考え方は必要になります。
ベクトルの内積①
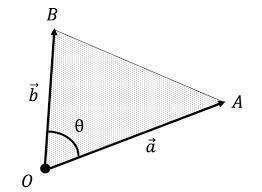
定義
余弦定理を用いて、
$$
BA^2=OA^2+OB^2-2×OA×OBcosθ
$$
また、ベクトルを用いて表すと
$$
|b⃗ –a⃗ |^2=|a⃗ |^2+|b⃗ |^2–2|a⃗ ||b⃗ |cosθ…①
$$
となります。
※注意
$$
a⃗ = 0 または b⃗=0 のときは、a⃗とb⃗の内積は定まらない。
$$
というのは、どちらかの長さがなければ角度は存在しません。
ベクトルの内積②
①より
$$
a⃗=(a_1,a_2) b⃗=(b_1,b_2)のとき a⃗・b⃗=a_1b_1+a_2b_2
$$
となります。
内分点の位置ベクトル
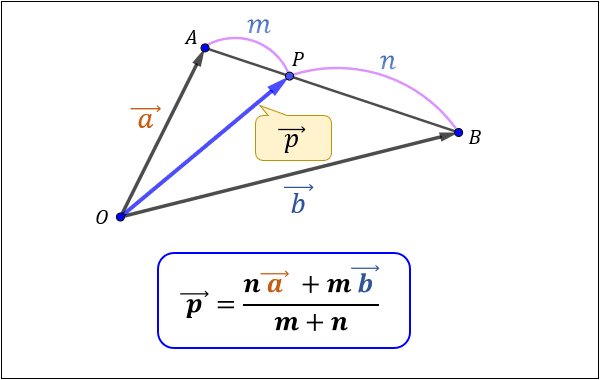
公式
$$
p⃗=\text{\(\frac {na⃗+mb⃗} {m+n}\)}
$$
公式はこのようになります。
証明
$$
AP^→=\text{\(\frac m {m+n}\)}AB^→
$$
ベクトルの減法を使うと次のようになる
$$
p⃗ –a⃗ =\text{\(\frac m {m+n}\)}(b⃗ –a⃗ )
$$
$$
p⃗ =(1-\text{\(\frac m {m+n}\)})a⃗+\text{\(\frac m {m+n}\)}b⃗
$$
$$
p⃗ =\text{\(\frac {na⃗ +mb⃗} {m+n}\)}
$$
これで証明は完了です。
外分点の位置ベクトル
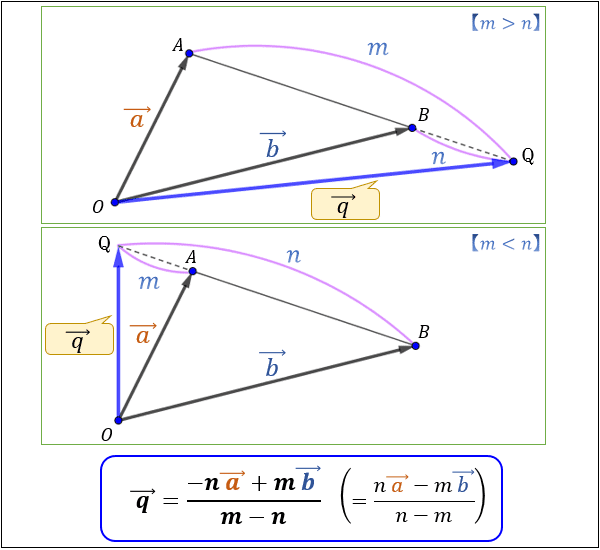
公式
$$
q⃗ =\text{\(\frac {-na⃗+mb⃗} {m-n}\)}
$$
証明①(m>n)
$$
AQ^→=\text{\(\frac m {m-n}\)}AB^→
$$
ベクトルの減法
$$
q⃗ –a⃗ =\text{\(\frac m {m-n}\)}(b⃗ –a⃗ )
$$
$$
p⃗ =(1-\text{\(\frac m {m-n}\)})a⃗+\text{\(\frac m {m-n}\)}b⃗
$$
$$
q⃗ =\text{\(\frac {-na⃗ +mb⃗} {m-n}\)}
$$
証明②(m<n)
$$
AQ^→=\text{\(\frac m {n-m}\)}BA^→\text{\(\frac m {m-n}\)}AB^→
$$
となるので、証明①と同じく
$$
q⃗ =\text{\(\frac {-na⃗ +mb⃗} {m-n}\)}
$$
となる。
