天才も様々。全く理解不能の人もいる。ラマヌジャン。

オイラーの公式は（後知恵なら）凡人にも思考を追いかけられる。

指数関数は微分しても形が変わらない関数です。

三角関数（sin,cos）は微分すると相互に入れ替わる関数です。その周期がπ。

だからeがsinとcosの和で表されて、周期πを突っ込めば－１になるのは、ある程度予想ができる。

＊＊＊

問題（？）は上の方、ラマヌジャンの円周率の公式です。

なんだこれ？

何をどうしたら、この式を思いつきますかね？

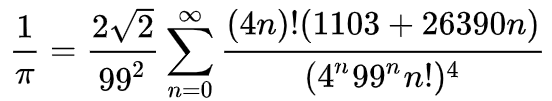
このパターンもあります。

普通、26390とか882なんて、わけのわからない生々しい数字は数学に出てこないと思うのですが、、、

というわけで、ラマヌジャンは凡人の上の上に立つ超天才なのだと思います。

インド人はすごい＾＾

＊＊＊

シュリニヴァーサ・アイヤンガル・ラマヌジャン（Srinivasa Aiyangar Ramanujan、1887年12月22日 - 1920年4月26日）

３２歳で夭折しました。

惜しい。実に惜しい人材です。

死因は結核とか肝炎とか言われていますが、正確なところは不明です。

私は、頭を使いすぎて過労で死んだのではないかと、冗談抜きで思っています。「３０時間ぶっ通しで考え続ける」なんてことが日常茶飯事だったらしい。

そりゃ、疲れるでしょ＾＾；