
コラッツ数列の最大値とメルセンヌ数の最大値の比例関係
ボトムアップ方式でコラッツテーブルを生成できるだけでは、コラッツ予想を証明したことにならないと言う意見があるので、ここではその任意の数のコラッツ数列における最大値と、その任意の数の2進桁のメルセンヌ数の最大値に比例関係があるので、任意の最大値までコラッツテーブルを生成できることがコラッツ予想を証明していることを説明する。
メルセンヌ数15まで
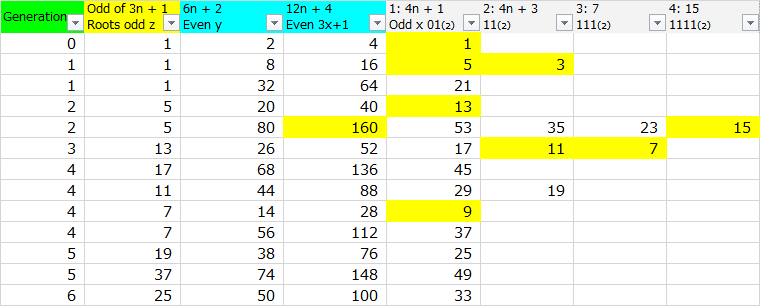
15まで、2進数で4桁までの初期奇数をボトムアップ方式で生成するための、15の”Even 3x+1”の最大値は160である。 これは任意の奇数の2進桁のメルセンヌ数の行の最大値までコラッツテーブルをジェネレートするとコラッツ数列を形成できることを意味する。
メルセンヌ数255まで

255まで、2進数で8桁までの初期奇数をボトムアップで生成するための、255の”Even 3x+1”の最大値は13,120である。 この中に27のコラッツ数例の最大値9,232がある。 27は2進数で5桁なのでメルセンヌ数で31であるが、31の行には2進数で8桁の161が含まれるので、メルセンヌ数255の行の最大値13,120までコラッツテーブルをジェネレートすると、27や31がリンクする。

これは、コラッツ数列27ー41の41や31ーー161の161など、2進数で5桁の任意の奇数をリンクする為の行が7桁の127では出揃わないからである。
メルセンヌ数131,071まで

メルセンヌ数31の行には2進数で8桁の161が含まれるように、コラッツ数列は2進木ではないので完全には一致しないが、メルセンヌ数の行の最大値と任意の数のコラッツ数列の最大値には比例関係がある。

まとめ
メルセンヌ数の行の最大値とコラッツ数列の最大値に比例関係があることで、任意の初期奇数の桁数からコラッツテーブルを生成するための、最大値制限を掛けれることが解るので、1からボトムアップ方式ですべての奇数が一回づつしか現れないことが保証されているコラッツテーブルを生成できることが、コラッツ予想の証明になってることと考えられる。この関係は現在計算で確かめられてる2⁶⁸以上の数値でも同じである。
ご意見があれば、コメントください。
