PID制御の作法　実践編　Part1

Part3、Part4では車の速度や位置を制御するためのチューニング手法を紹介してきました。

今回は実践編ということで、実際にチューニング方法が狙いどおりの性能を発揮するかを見ていきましょう。

実践編第１回目は車の速度制御です。

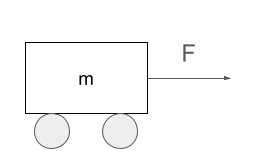
運動方程式は$${ma=F}$$となりますので
加速度$${a}$$は
$${a=\frac{F}{m}}$$
加速度を積分することで車の速度$${v}$$が算出できます。

車にかける力を比例先行型PI制御で決定することにします。
$${F=-K_pv+K_i\int{(v_t-v)}}$$

ここで２次伝達関数となるため、オーバーシュートしないようなPIゲインを算出すると
$${K_p=4{\pi}f_cm}$$
$${K_i=4\pi^2f_c^2m}$$

詳しくは下記記事を参考にしてください。

ここで車の質量$${m}$$は1980[kg]の車だとしましょう。
PIゲインはカットオフ周波数$${f_c}$$だけを設定するだけで良いことになります。

ではシミュレーションを実際にしてみましょう。
カットオフ周波数を$${f_c=0.1[Hz]}$$にした結果です。
目標値は1[s]でステップ上に100[km/h]になるように入力します。

fc=0.1[Hz]

では次はもっと応答を早くしてみましょう。
カットオフ周波数を$${f_c=1[Hz]}$$にした結果です。

fc=1[Hz]

目標値の100[km/h]に到達するまでの時間が早くなりました。
また両方ともオーバーシュートなく目標車速にコントロールできています。

ではPIゲインが適切でない場合はどうなるでしょうか？

$${K_p=4{\pi} 0.01m}$$
$${K_i=4\pi^2 0.1^2m}$$
とそれぞれ設定してみましょう。

Kp:fc=0.01[Hz] Ki:fc=0.1[Hz]

オーバーシュートしてかつ振動してしまいました。
こんな車に乗っていたら車酔いをしてしまいますね。

このようにカットオフ周波数を変えるだけで安定性を損なわずにゲイン設定を決めることができます。

次回は車の位置制御のシミュレーションをやってみたいと思います。