
K2, at 8,611 metres (28,251 ft) above sea level lying in the northwestern Karakoram Range, is the second-highest mountain on Earth and is so attractive but deadly challenging.

The title⬆️ in German is Berg der Berge, not Der Zauberberg (The Magic Mountain)😎


K3 is a different peak but is an equally beautiful object in mathematics.
Let's not be confused with 3K (a word coined in Japanese), which in English is expressed as 3D = Dirty, Dangerous and Demanding (or Demeaning), utterly inappropriate for this article.
https://x.com/SokoKhazar/status/1731290460650614827

Dans la seconde partie de mon rapport, il s'agit des variétés kählériennes dites K3, ainsi nommées en l'honneur de Kummer, Kähler, Kodaira et de la belle montagne K2 au Cachemire.

This sentence by André Weil (6 May 1906 – 6 August 1998) is so beautiful with full respect to the following mathematicians:
Ernst Eduard Kummer (29 January 1810 – 14 May 1893)
Erich Kähler (16 January 1906 – 31 May 2000)
Kunihiko Kodaira 小平邦彦 (16 March 1915 – 26 July 1997)
Kummer surfaces are examples of K3 surfaces, which are the Calabi–Yau manifolds (and also the hyperkähler manifolds) of dimension two, fully investigated by Kunihiko Kodaira. While we call them surfaces, they are 2-complex dimensional, therefore, 4-real dimensional.
I was extremely fortunate to attend Professor Kodaira's special lecture on "Deformation of Complex Manifolds" in the early summer of 1980.
The definition of (algebraic) K3 surface is quite simple:
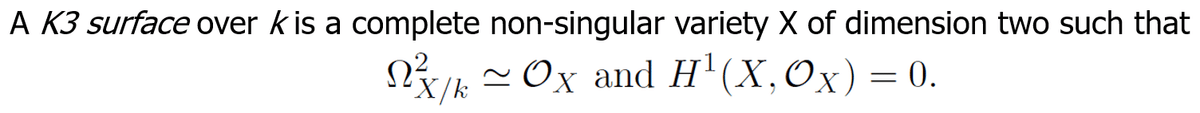
As I added the adjective "algebraic" for the definition, non-algebraic K3 surfaces do exist.
I only studied K3 surfaces at introductory level, but it is very enchanting. It is also intriguing that K3 surfaces have been studied from various perspectives.
As the following picture shows, it appears in many areas in mathematics (and physics).
Brown University
I found a very interesting and very convincing post in response to the question "Why does so much recent work involve K3 surfaces?", an old question dating back to March 2011:

https://mathoverflow.net/questions/59347/why-does-so-much-recent-work-involve-k3-surfaces
Here "La conjecture de Weil" is NOT "The Taniyama–Shimura–Weil conjecture" about elliptic curves proved by Andrew Wiles and others resulting in a proof of Fermat's Last Theorem (FLT), but is a conjecture by André Weil (who named K3 surface) relative to properties of zeta function of a non-singular projective algebraic variety over a finite field:
Header Image Credit: Pinterest
P.2. ① I like the following quote, too:
Dieu existe parce que les mathématiques sont cohérentes, et le Diable existe, puisque nous ne pouvons pas le prouver.
The statement sounds like intended to ridicule those who pervert Gödel's incompleteness theorems in attempt to tarnish or deny accomplishments in mathematics.
Incidentally, the adjective cohérent/cohérente (in French, coherent in English) appears as a noun in "Théorème de cohérence d'Oka" for Œuvres principales:
https://fr.wikipedia.org/wiki/Kiyoshi_Oka
I know that there're so many Japanese who refer to Kiyoshi Oka 岡潔 but in a different context.
P.S. ② K2 is a literally dangerous mountain:
https://twitter.com/SokoKhazar/status/1825095301637783682
■
