
📏エルゴード性とは統計的な均質性
先に示したように、我々の目的のために離散的なソースはマルコフ過程によって表現されると考えることができる。可能な離散マルコフ過程の中に、通信理論で重要な特別な特性を持つグループがある。この特別なクラスは「エルゴード」過程からなり、対応するソースをエルゴード情報源と呼ぶことにする。
大雑把に言えば、エルゴード的性質とは統計的な均質性を意味する。
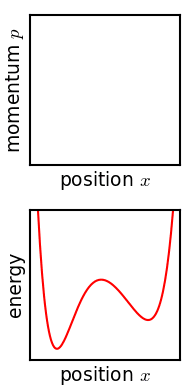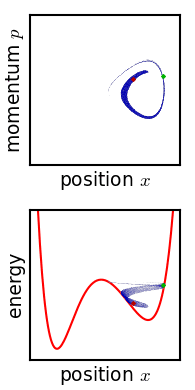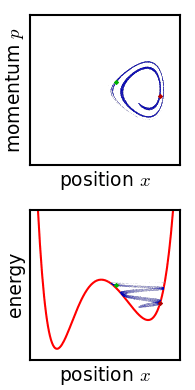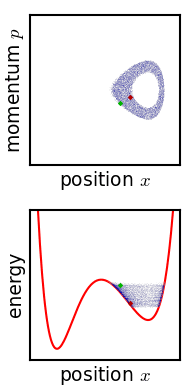
エルゴード理論の中心的な関心は、力学系を長時間実行させたときの挙動である。ポアンカレ回帰定理は、位相空間の任意の部分集合に含まれるほぼすべての点が、最終的にその部分集合を再訪することを主張するもので、この方向での最初の成果である。ポアンカレ漸化式が成り立つ系は保存系であり、したがってすべてのエルゴード系は保存系である。
中学生レベルでわかるように、エルゴード理論に関する説明を以下にまとめました。
### エルゴード理論
- **エルゴード理論**:物事が長い時間にわたってどう動くかを研究する学問です。特に、力学系という、時間とともに変化するシステムを見ます。
### ポアンカレ回帰定理
- **ポアンカレ回帰定理**:あるシステムがどう動くかを考えたとき、ほとんどすべての点が最終的に元の場所に戻ってくることを示した定理です。たとえば、風船の中の空気分子がどこに行っても、最終的には元の位置に戻ってくるような感じです。
### 保存系
- **保存系**:システムの中でエネルギーや物質の量が変わらないシステムのことです。たとえば、閉じた箱の中での空気分子の運動などです。
### エルゴード系
- **エルゴード系**:長い時間が経つと、システムのどの部分にもほぼ均等に分布するようなシステムのことです。保存系の中に含まれています。
これらの概念は、物事がどのように動き、時間が経つとどうなるのかを理解するのに役立ちます。
エルゴード性の概念とエルゴード仮説は、エルゴード理論の応用の中心である。その根底にある考え方は、ある種の系では、その特性の時間平均は空間全体の平均に等しいということである。
量子論のエルゴード定理との違い
エルゴード定理とエルゴード性は、それぞれ異なる数学的な文脈で使用される概念ですが、その背後にある基本的なアイディアや哲学には関連性があります。両方の概念は、ある種の「平均的な」振る舞いや長期的な振る舞いに関するものです。
量子論のエルゴード定理:
この文脈でのエルゴード定理は、ある特定の条件の下で、物理システムの時間平均が空間平均と等しくなることを示します。言い換えれば、長期的な観察は、システム全体の一瞬一瞬のスナップショットを平均するのと同じ情報を提供するという考え方です。
シャノンの情報理論におけるエルゴード性:
シャノンの情報理論でのエルゴード性は、情報源が時間的に「平均的に」一定の振る舞いを示すことを意味します。エルゴード的な情報源において、長期的なサンプルのエントロピー(平均情報量)は、任意の瞬間のサンプルのエントロピーと一致します。
関連性:
両方の概念は、システムや情報源の「長期的な」または「平均的な」振る舞いに関心があります。エルゴード的な性質を持つシステムは、時間的に平均したときの振る舞いが、異なる場所や状態の空間的な平均と一致するという特性を持っています。
クロード・シャノンは情報の数学的理論を発展させる中で、エルゴード理論を取り上げたのはいくつかの理由があります。
情報源のモデリング: シャノンは情報源を確率的な過程としてモデル化していました。エルゴード過程は長い時間の平均が空間的平均と一致するという性質を持つため、情報源の長期的な振る舞いを特徴づけるのに適しています。この性質により、情報源のサンプルの一部を取ることで、全体の平均的な情報量を推定することができます。
エントロピーの計算: シャノンの情報量の定義は確率変数の確率分布に基づいています。エルゴード性の仮定の下では、長期的な観測を通じて得られる平均的な情報量が全体のエントロピーと一致すると見なすことができます。
情報伝達の理論的基盤: シャノンの情報理論は、情報を伝達する過程における不確実性を量るためのものです。エルゴード性は、情報伝達の不確実性が時間とともに一定に保たれることを保証する役割を果たします。
エルゴード性は情報のエントロピーを計算する際の便利な前提となっています。エルゴード的な情報源の場合、時間的な平均が空間的な平均と一致するという性質があります。これにより、長期的な観測から得られる情報の平均量が、その情報源全体のエントロピーと一致すると考えることができます。この前提のもとで、エントロピーの計算や情報伝達の最適性を議論することができるのです。
いいなと思ったら応援しよう!

