
イラレのアピアランスで段落に斜体をかけたい!!【Adobe illustrator】
Adobe illustratorを使っていて、イタリック体がない日本語書体などの文字に斜体をかけたいと思ったことはありませんか?

こんな感じで、引用文などの段落全体に斜体をかけたい!というシーン、結構あると思います。
でもこの操作、需要が多いはずなのにデフォルトの機能としては用意されていないんですよね……
これがcssなら
{font-style: italic;}で一発なのですが……。
「イラレ 斜体」で検索すると多くの方がこの問題に対するアイディアを公開されていますが、どれも一長一短なところがあります。この記事では、それらのアイディアを参考にしつつ、特に段落全体にアピアランスを使って斜体をかける方法についてご紹介します。
前提説明は抜きに具体的な解決策を見たい方は目次から「解決策-アピアランスで段落に斜体を適用する方法」まで飛んでください。
よく見かける方法と問題点
【1】変形 >シアーを使う方法
こちらで紹介されているような最も一般的なアイディアです。

メリット
▪️直感的に角度を指定できる
▪️デフォルトの機能で完結デメリット
▪️一度適用してしまうと数値が残らない(破壊編集)ので元に戻したくなった時に不便
▪️1行の単語や文にしか適用できない

これの解決策については後述します。
【2】変形>3Dを使った擬似シアー
こちらで紹介されています。
効果>3D>回転から、x軸とy軸に回転をかけることで擬似的に斜体を表現できます。

メリット
▪️デフォルトの機能で完結
▪️3D回転機能はアピアランスパネルにもあるので、非破壊編集が可能。いつでも簡単に数値を修正したり、元に戻したりすることができるデメリット
▪️1行の単語や文にしか適用できない
▪️3D処理は多用すると重い
▪️傾ける角度が直感的に分かりづらい(10°と入力しても、見た目が10°傾くわけではない)
▪️三次元的に回転しているので、歪む(全体が小さくなる)

3D回転を使うと回転した分縮んで見えてしまう
アピアランスで実装できるので便利ですが、想定しているレイアウト(テキストボックスのサイズ)やフォントサイズに対して縮んで見えてしまうのがやや扱いづらいところです。歪みは回転角度が大きければ大きいほど強くなります。
問題のまとめ
変形>シアー機能ではシアー角度が保存されないので後から調整しづらい
アピアランスパネルにはシアー機能がない
3D回転効果を適用してアピアランスによる擬似シアーを実装できるが、角度が直感的ではなく、フォントサイズや全体の大きさが変わってしまう
シアー機能や3D回転では1行にしか対応できず、複数行の段落になると行頭・行末が揃わない
解決策-アピアランスで段落に斜体を適用する方法
【1】アピアランスの重ねがけでシアーを再現するスクリプト
「アピアランス>変形」を2回重ねがけすることでシアーを再現できます。
拡大縮小と回転を組み合わせて任意の角度のシアーを再現するためにはそこそこの行列計算が必要になりますが(おまけ参照)、あるふぁさんによる「アピアランスでシアー(水平)計算機」に角度を入力すると、簡単な操作で必要な数値を取得できます。
さらにこちらのスクリプト版を使えばイラレ上でボタンを押して角度を入力するだけで即座にアピアランスが適用されます。ありがたいですね。

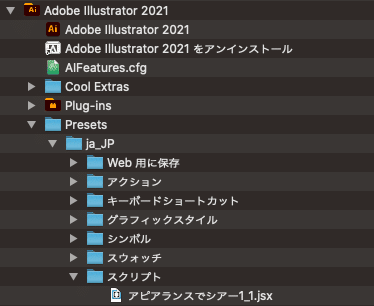
[ダウンロード]をクリックして入手した「アピアランスでシアー1_1.jsx」を、
/Adobe Illustrator 2021/Presets/ja_JP/スクリプト/
のフォルダ内に配置。あとはillustratorを再起動すると、スクリプトを使用できるようになります。

斜体にしたいテキストを選択した状態で「ファイル>スクリプト>アピアランスでシアー1_1」と進むとウィンドウが起動。傾けたい角度を入力して「OK」を押すと……

自動で「変形」アピアランスが2つ追加され斜体になりました!
【2】複数行の段落に斜体をかける
このスクリプトを複数行の段落に適用してみます。(わかりやすくするためにテキストボックスと同じサイズの水色の背景を置いています)

スクリプトで20°のシアーをかけると……

テキストボックスごと変形されてしまうため、行頭・行末が揃いません。
解決策は単純で、元となるテキストボックスに反対向きのシアーをかけて行をずらしておくことでテキストボックスの歪みを相殺します。
①段落をレイアウトしたいサイズの長方形を用意する

②長方形に「変形>シアー」を適用
今回は20°の斜体をかけたいので、あらかじめ-20°のシアーをかけておくことでズレを相殺します。
かけたい斜体と同じ角度、逆向きの値を入力しましょう。

③平行四辺形をテキストボックス化する
テキストツールで平行四辺形の辺(パス)をクリックすると、図形がテキストボックス化します。
この時、行頭・行末は平行にズレているが、文字にはシアー(斜体)がかかっていないのがポイントです。


④スクリプトを使ってアピアランスによるシアー(斜体)をかける
先ほど紹介したスクリプト「アピアランスでシアー」を使ってテキストに20°の斜体をかけます。

あらかじめズラしたテキストボックスにスクリプトを適用すると……


行頭・行末が揃ったまま斜体がかけられた段落が完成!!
元々の想定レイアウト(水色の長方形)にピッタリ収まっており、フォントサイズもそのままです。
この手法のポイントは必ず
長方形を用意し逆向きのシアーをかける
図形をテキストボックス化する
テキストボックスにシアーをかける
の手順で行うことです。
先にテキストボックスになったものに逆シアーをかけると、文字自体に斜体がかかってしまいうまくいきません。
まとめ
①段落をレイアウトしたいサイズの長方形を用意する
②かけたい斜体と逆向き、同角度のシアーを長方形に適用
③平行四辺形をテキストボックス化する
④「アピアランスでシアー」スクリプトで斜体をかける
斜体角度を変更したいときや元に戻したいときはアピアランスを解除・削除・再適用することで値の変更が可能です。
②で行をズラすときにシアー機能を使っているので結局完全な非破壊編集にはなっていない(自由に解除はできない)んですけどね。
こればっかりはAdobeさんが段落に斜体をかける機能を実装してくれるのを待ちましょう。
何かもっとスマートな方法があればぜひ教えてください。
おまけ
「拡大縮小」+「回転」の重ねがけでシアーが再現できる理由
ここから先は数学、理論のお話なので興味がある方以外はスキップしてください。
「アピアランスでシアー」の各変形の数値(拡大率や回転角度)は行列計算により求めることができます。シアー変換行列と同値な「拡大縮小+回転」変換行列を、連立方程式を解くことにより求める過程を説明していきます。
アフィン変換、線形変換と変換行列の一般形
拡大縮小、回転、シアーはいずれもアフィン変換という計算処理に該当します。画像のアフィン変換は対象の画像の2次元座標に変換行列を掛ける行列の掛け算です。
$$
\begin{pmatrix}
x'\\
y'
\end{pmatrix}
=
\begin{pmatrix}
a & b\\
c & d
\end{pmatrix}
\begin{pmatrix}
x\\
y
\end{pmatrix}
+
\begin{pmatrix}
e\\
f
\end{pmatrix}
$$
アフィン変換の一般式。(x,y)は元画像上の座標。(x',y')は変換後の座標。
ここで、$${(e,f)}$$の足し算は平行移動に相当する計算なので、今回使わないこの部分を無視すると式は以下のように単純な積の形になります。拡大縮小、回転、シアーをまとめて$${a,b,c,d}$$4つのパラメータで表した以下のような行列計算を線形変換といいます。線形変換はアフィン変換の特殊な場合です。
$$
\begin{pmatrix}
x'\\
y'
\end{pmatrix}
=
\begin{pmatrix}
a & b\\
c & d
\end{pmatrix}
\begin{pmatrix}
x\\
y
\end{pmatrix}
$$
さて、今回のように水平方向にシアーをかけたい場合、$${y}$$座標が$${y_1}$$である点の画像を水平方向に$${my_1}$$だけズラせばいいということになります。($${m}$$はシアー角により変わる定数です。)

線形変換行列で表現すると
$$
\begin{align*}
\begin{pmatrix}
x'\\
y'
\end{pmatrix}
=
\begin{pmatrix}
1 & m\\
0 & 1
\end{pmatrix}
\begin{pmatrix}
x\\
y
\end{pmatrix}
\\
=
\begin{pmatrix}
x+my\\
y
\end{pmatrix}\tag{1}
\end{align*}
$$
となります。
一方で、$${x}$$軸方向に$${a}$$、$${y}$$軸方向に$${b}$$だけ拡大する変換の行列計算は
$$
\begin{pmatrix}
x'\\
y'
\end{pmatrix}
=
\begin{pmatrix}
a & 0\\
0 & b
\end{pmatrix}
\begin{pmatrix}
x\\
y
\end{pmatrix}\tag{2}
$$
また、任意の角度$${θ}$$だけ回転する行列計算は
$$
\begin{pmatrix}
x'\\
y'
\end{pmatrix}
=
\begin{pmatrix}
\cos{θ} & -\sin{θ}\\
\sin{θ} & \cos{θ}
\end{pmatrix}
\begin{pmatrix}
x\\
y
\end{pmatrix}\tag{3}
$$
のように書けます。拡大縮小と回転を同時に行う場合、これらの式の変換行列の部分を積の形でまとめると
$$
\begin{align*}
\begin{pmatrix}
a & 0\\
0 & b
\end{pmatrix}
\begin{pmatrix}
\cos{θ} &-\sin{θ}\\
\sin{θ} & \cos{θ}
\end{pmatrix}
=
\begin{pmatrix}
a\cos{θ} & -a\sin{θ}\\
b\sin{θ} & b\cos{θ}
\end{pmatrix}\tag{4}
\end{align*}
$$
のようになります。
シアー行列と同値な「拡大縮小+回転」行列の組を求める
今回の課題は『「拡大縮小」+「回転」の重ねがけでシアーを再現』することでしたから、変換行列(4)の1つ目を$${\mathbf{A} _1}$$、2つ目を$${\mathbf{A} _2}$$としたとき、シアー変換式(1)と比較して
$$
\mathbf{A}_1
\mathbf{A}_2
=
\begin{pmatrix}
1 & m\\
0 & 1
\end{pmatrix}\tag{5}
$$
となるような変換行列$${\mathbf{A} _1}$$,$${\mathbf{A} _2}$$を用意すればいいことになります。以下、2つの行列のパラメータをそれぞれ
$$
\mathbf{A} _1
=
\begin{pmatrix}
a\cos{θ} & -a\sin{θ}\\
b\sin{θ} & b\cos{θ}
\end{pmatrix}\tag{6}
$$
$$
\mathbf{A} _2
=
\begin{pmatrix}
c\cos{φ} & -c\sin{φ}\\
d\sin{φ} & d\cos{φ}
\end{pmatrix}\tag{7}
$$
とすることにします。
これらの行列の積$${\mathbf{A}_1\mathbf{A}_2}$$を頑張って計算すると
$$
\begin{align*}
\mathbf{A}_1
\mathbf{A}_2
=
\begin{pmatrix}
a\cos{θ} & -a\sin{θ} \\
b\sin{θ} & b\cos{θ}
\end{pmatrix}
\begin{pmatrix}
c\cos{φ} & -c\sin{φ}\\
d\sin{φ} & d\cos{φ}
\end{pmatrix}\\
=
\begin{pmatrix}
a\cos{θ} c\cos{φ} -a\sin{θ} d\sin{φ}
&-a\cos{θ}c\sin{φ} -a\sin{θ}d\cos{φ}\\
b\sin{θ}c\cos{φ} +b\cos{θ}d\sin{φ}
&-b\sin{θ}c\sin{φ} +b\cos{θ}d\cos{φ}
\end{pmatrix}\tag{8}
\end{align*}
$$
となります。式(5)と(8)の比較から
$$
\begin{cases}
a\cos{θ}{\cdot}c\cos{φ} -a\sin{θ}{\cdot}d\sin{φ}=1\\
-a\cos{θ}{\cdot}c\sin{φ} -a\sin{θ}{\cdot}d\cos{φ}=m\\
b\sin{θ}{\cdot}c\cos{φ} +b\cos{θ}{\cdot}d\sin{φ}=0\\
-b\sin{θ}{\cdot}c\sin{φ} +b\cos{θ}{\cdot}d\cos{φ}=1
\end{cases}
$$
となり、結局これら4つの方程式から値$${(a,b,c,d,θ,φ)}$$を求めればいいことがわかります。
連立方程式を解く
さて、6文字の連立方程式で4式しかない場合、解の自由度が2となるので、このような変形を実現する行列の組み合わせ$${\mathbf{A} _1}$$,$${\mathbf{A} _2}$$は1種類に定まりません。
逆にいうと、値$${(a,b,c,d,θ,φ)}$$のうち2つを任意に定めることで無限にある組み合わせの中から特定の1組を求めることができるということになります。
以下ではまず、計算を簡単にするため$${\cos{φ}=\sin{φ}={1\above{1pt}\sqrt{2}}}$$となる場合を考えることとします。
$$
\begin{align*}
\cos{φ}=\sin{φ}={1\above{1pt}\sqrt{2}}\\
\therefore
φ=45^{○}
\end{align*}
$$
このとき、連立方程式の各式を$${\cos{φ}=\sin{φ}}$$で辺々割ることにより
$$
ac~\cos{θ} -ad~\sin{θ}=\sqrt{2}\tag*{①}
$$
$$
-ac~\cos{θ} -ad~\sin{θ}=\sqrt{2}m\tag*{②}
$$
$$
bc~\sin{θ} +bd~\cos{θ}=0\tag*{③}
$$
$$
-bc~\sin{θ} +bd~\cos{θ}=\sqrt{2}\tag*{④}
$$
を得ます。
①+②および①-②から
$$
ad~\mathrm{sin}θ=-{\sqrt{2}\above{1pt}2}(1+m)\tag*{⑤}
$$
$$
ac~\cos{θ}={\sqrt{2}\above{1pt}2}(1-m)\tag*{⑥}
$$
同様に③+④および③-④から
$$
bd~\cos{θ}={\sqrt{2}\above{1pt}2}\tag*{⑦}
$$
$$
bc~\sin{θ}=-{\sqrt{2}\above{1pt}2}\tag*{⑧}
$$
⑤,⑧と⑥,⑦の組を辺々割ることでそれぞれ$${\sin{θ}}$$,$${\cos{θ}}$$を消去して
$$
{ad\above{1pt}bc}=1+m\tag*{⑨}
$$
$$
{ac\above{1pt}bd}=1-m\tag*{⑩}
$$
⑨+⑩より$${m}$$を消去すると
$$
{a\above{1pt}bcd}(c^{2}+d^{2})=2\tag*{⑪}
$$
また、⑦,⑧および$${\sin^{2}θ+\cos^{2}θ=1}$$より
$$
{1\above{1pt}{2b^{2}c^{2}}}+{1\above{1pt}{2b^{2}d^{2}}}=1
$$
辺々$${2b^{2}c^{2}d^{2}}$$をかけると
$$
c^{2}+d^{2}=2b^{2}c^{2}d^{2}\tag*{⑫}
$$
⑪に⑫を代入して整理すると
$$
abcd =1\tag*{⑬}
$$
を得ます。残る自由度は1なので、さらに計算を簡単にするため以下では$${d=1}$$($${\Harr}$$変形2ではy軸方向の拡大縮小をしない)とします。
⑨,⑩,⑬より
$$
\begin{cases}
a=(1+m)bc\\
ac=(1-m)b\\
abc=1
\end{cases}
$$
と$${a,b,c}$$3文字に対する3式の連立方程式($${m}$$は定数)が得られれ、これらを解くことにより
$$
c=\sqrt{\displaystyle\frac{1-m}{1+m}}~,\quad
b=\displaystyle\frac{1}{\sqrt{1-m}}~,\quad
a=\sqrt{1+m}
$$
が分かります。
さらに⑦と$${d=1}$$より
$$
\begin{align*}
\cos{θ}={1\above{1pt}\sqrt{2}b}\\
={\sqrt{1-m\above{1pt}2}}
\end{align*}
$$
であり、すなわち
$$
θ= \arccos\bigg({\sqrt{1-m\above{1pt}2}}\bigg)
$$
となります。

ここで、目的のシアー角度(シアーにより傾いた鉛直線とy軸とのなす角度)を$${\alpha}$$とすると、図より
$$
m=\tan\alpha
$$
です。
計算結果まとめ
以上の結果をまとめると、水平方向に任意の角度$${\alpha}$$だけ傾けるシアー変形と同値となる線形変換は以下のようになります。
$$
\begin{pmatrix}
\sqrt{1+\tan\alpha} & 0\\
0 & \displaystyle\frac{1}{\sqrt{1-\tan\alpha}}
\end{pmatrix}
\begin{pmatrix}
\cos{θ} & -\sin{θ}\\
\sin{θ} & \cos{θ}
\end{pmatrix}\\
$$
$$
\times
\begin{pmatrix}
\displaystyle\sqrt{\frac{1-\tan\alpha}{1+\tan\alpha}}& 0\\
0 & 1
\end{pmatrix}
\begin{pmatrix}
\cos{45^{○}} & -\sin{45^{○}}\\
\sin{45^{○}} & \cos{45^{○}}
\end{pmatrix}
$$
$$
ただし,θ= \arccos\bigg({\sqrt{1-m\above{1pt}2}}\bigg)
$$
「アピアランスでシアー」計算公式
illustratorの「変形」メニューの記法に合わせると必要な変形は以下のようになります。
変形1
拡大縮小(水平方向):拡大率$${=\sqrt{1+\tan\alpha}}$$
拡大縮小(垂直方向):拡大率$${=\displaystyle\frac{1}{\sqrt{1-\tan\alpha}}}$$
回転:角度=$${\arccos\bigg(\sqrt{\displaystyle\frac{1-\tan\alpha}{2}}\bigg)}$$
変形2
拡大縮小(水平方向):拡大率$${=\displaystyle\sqrt{\frac{1-\tan\alpha}{1+\tan\alpha}}}$$
拡大縮小(垂直方向):拡大率$${=100\%}$$
回転:角度=$${45^{○}}$$

この式を使ってExcelなどで計算してあげると自力でもシアーを再現することができます。
※あるふぁさんによる「アピアランスでシアー(水平)計算機」では変形2の角度を「$${-45^{○}}$$」、水平方向の拡大率を$${c=1}$$で固定しているため、パラメータの設定が微妙に異なりますが、計算方法は同じです。
変形1
拡大縮小(水平方向):拡大率$${=\displaystyle\frac{1}{\sqrt{1+\tan\alpha}}}$$
拡大縮小(垂直方向):拡大率$${=\sqrt{1-\tan\alpha}}$$
回転:角度=$${\arccos\bigg(\sqrt{\displaystyle\frac{1+\tan\alpha}{2}}\bigg)}$$
変形2
拡大縮小(水平方向):拡大率$${=100\%}$$
拡大縮小(垂直方向):拡大率$${=\displaystyle\sqrt{\frac{1+\tan\alpha}{1-\tan\alpha}}}$$
回転:角度=$${-45^{○}}$$
