コンセンサスゲームと対話の重要性
人と知に関するラジリア会の第1回目は集合知について考えました.集合知とはたくさんの意見や知性がまとまったうえで振る舞う知能のことです.
今回は集合知を体験するためにコンセンサゲームを行いました.雪山のコンセンサスゲームはこちら

10個のアイテムの優先順位をまずは個人で考えて,その後4名ほどのグループに分かれます.そのグループで意見をすり合わせてグループとしての意思決定をして順位をつけてもらいます.このときのコツは安易な多数決には頼らずに全員が納得いくまで話し合うことです.

グループで意見がまとまったら結果発表になります.このゲームは専門家による模範解答があり.模範解答とのずれが小さいほど優れた結果であると言えます.ここで参加者の方に自分一人で考えた優先順位と,グループワークで合意した回答のどちらがより優れた回答になったか比較していただきました.するとなんと大抵の人がグループで出した結論のほうがより良いものになっていました.ということでグループワークは大切です.皆さんもっと普段からいろいろ話し合いましょう★.めでたしめでたし・・・
で終わるのがインターンや企業研修,学校の授業などの巷で行われているコンセンサスゲームである.だがラジリアはこれでは終わらない‼️.「さて,何故であろうか?」

実はこれこそが集合知のメカニズムであるのだが,ここではこんな解説を試みてみたい.有名な心強き諺である「三人寄れば文殊の知恵」である.

どういうことか?例を出そう.人が2択において正しい判断をする確立を6割と仮定する.(コイントスでは5割なので流石に人間の知能を信じたい)すると1人だけでは正答率は6割であるが3人集まって単純に多数決をすることによって約6割5分になる(上図の表を参照).6割ではなく8割なら3人寄ることで約9割になる.文殊の知恵と呼べるかは定かではないが,3人がよりきちんと話し合うことで見落としていた視点や意思決定の前提についてまで詳しく話し合えるのであればより確率は上がるであろう.
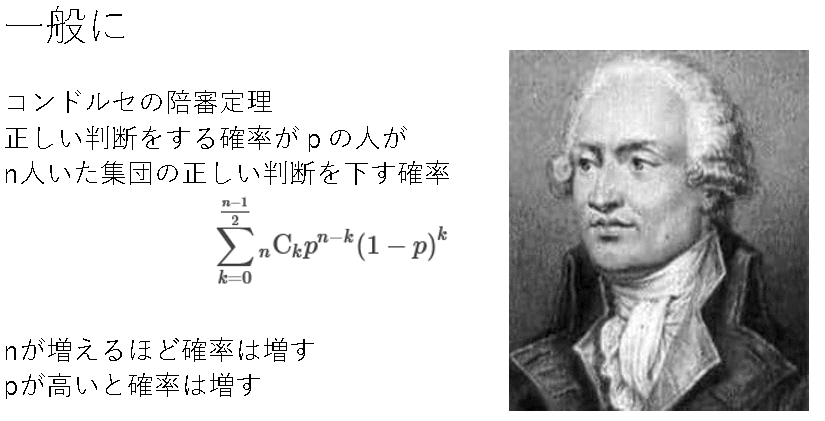
もちろん人数が増えたら正しい判断ができる確率は増える.また1人1人がじっくりと考えれば考えるほど全体の解が正しくなる可能性は高まる.一般にこれをコンドルセの陪審定理と呼ぶ.数式は高校数学程度の知識で理解できるはずだ.詳しく知りたい方はこちらの記事を参考にされたし.

さて,より良い意思決定のためには何が必要か話し合った.先ほどのコンドルセの陪審員の定理から得たものは,できるだけ多くの人が意思決定にかかわるということである.つまりは集合知を大切にすることだ.こちらのリンクをご覧ください.
ただ,集合知はいつでも正義なのか?投票やネット言論は時に間違うのではないか?正しい判断ができる確率が減ると逆に間違った答えに行きつく(p=0.5を切ると人が集まっても逆効果だ)船頭多くして船山に上るという状況になる.そこでしっかりと学び,考え,仲間と話す熟議が必要ではないか?
nを増やすのも大切だし,それぞれのpも高めることも必須である.学生団体ラジリアとしてなるべく多くの人と知についてじっくり話し,考え合うことも大切にして人と知の間にステキな反応を起こすということをモットーに活動して参りたい.
お読みくださってありがとうございます.学生団体ラジリアはステキな反応をおこす仲間を募集してます.
2021年7月追記
コンドルセの陪審定理でこのコンセンサスゲームで個人の判断が5割の確率で以上の正しさを誇るとは必ずしも言い切れません。ただ、コンセンサスゲームでは対話と熟議をすることによって個人の思い込みや偏見も客観的に検討することができるので正しい判断になりやすくなります。
ただ、人数が多すぎる場合、十分に話し合いをすることが難しく、四人程で行ったほうが良い結果になることが多いです。