ド・ブロイの「物質波」は、存在していない。

１８世紀頃まことしやかに信じられていた熱素のように、また相対論以前に信じられていた電磁波の媒体であるエーテルのように、ド・ブロイ波とも呼ばれるド・ブロイの物質波は、現代ではその存在が否定をされています。原子の中には実在としての物質波が充満しているわけではありません。前世紀から比べて、現代の量子力学の理解は進んでいます。

例えば電子の二重スリット実験も、物質波という実在で説明をすることは間違っています。

前世紀初頭の量子力学勃興期には概念の混乱が続きました。波動関数Ψは、物理的実在である物質波だと当初考えられたのですが、多粒子の量子力学を考えるとΨは多次元空間の関数ということになり、3次元空間中の物理的な波動とは解釈できなくなりました。例えば２粒子系の波動関数ではその引数が合計６個となる下記の複素関数になります。

従ってΨを３次元空間の物質波と解釈することが不可能となっています。また波動関数はそのような物理的な実在ではなく、下記記事にあるように情報的概念であることが、現在では分かっています。

「粒子ではなく物質波ψこそが実在であり、本質である。ただ観測すると因果律を破る速さでψが収縮することは、現在でも謎のままである」という内容の文章があったら、それは全く間違いだと言うことができます。現代の量子力学には、そのような「観測問題」は存在していないのです。

化学などの他分野では違うかもしれませんが、物理学科の教育として、「物質波」を扱う前期量子論は現在では全く不要です。古典力学の破綻を学生に伝えるだけで十分であり、「物質波」などの現在では間違っていた概念を今でも教えることは理解の混乱の元です。前期量子論は歴史ドラマとしては大変面白いのですが、その過程の話には現代からの視点では間違いが多過ぎます。

ただし「物質波」は否定をされましたが、所謂「ド・ブロイ関係式」は解釈を変えて、現代の量子力学や場の量子論の中に残っています。それは、自由粒子の平面波の波動関数の波数ｋと角振動数ωを、粒子の運動量pとエネルギーEに結びつける下記の関係式のことです。ド・ブロイは物質波の性質として、この関係式を提案しました。

現代の量子力学でも、このド・ブロイ関係式を満たす平面波の波動関数を任意の重みで重ね合わすことで、自由粒子の任意の波動関数を下記のように構成をすることができます。

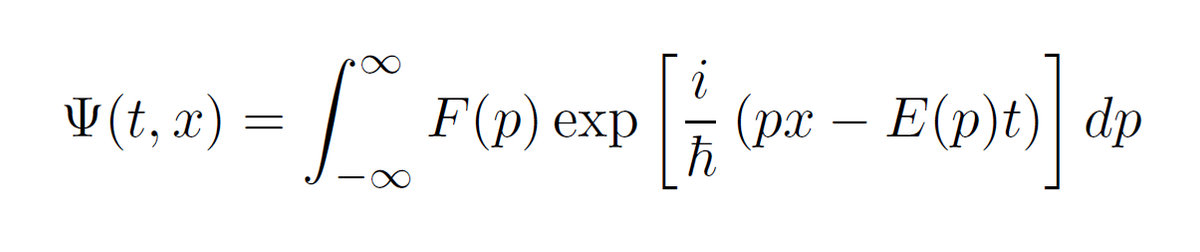
ここで重みの関数F(p)を運動量pに依存しない定数関数とすれば、その波動関数は初期時刻t=0にx=0へと局在をしたデルタ関数にできます。またF(p)を、幅Δｐが大きなガウス関数にすれば、波動関数は位置の幅Δｘが小さなガウス波束となります。また逆にΔｐが小さければ、波束の幅Δｘは大きくなります。この性質はすべてド・ブロイ関係式と重ね合わせの性質から理解ができます。その意味でド・ブロイ関係式は、現代でも物理学者に直観を与えるツールとして利用をされ続けています。

なお粒子の量子力学で、「量子重ね合わせを使って幅の狭い物質波の波束が作れるので、それが粒子であり、元は波だ」という説明も散見しますが、それは正しくないです。電子は低エネルギー領域において飽くまで「粒子」そのものであり、決して「物質波」や、その波束ではありません。

場の量子論では、ド・ブロイ型の平面波は場の演算子を展開するモード関数として現れます。

ド・ブロイの「物質波」は実在としては否定をされましたが、その間違ったイメージから提案をされた「ド・ブロイ関係式」自体は現代の物理学の中に意味のある形で生き残っています。「物質波」に関するド・ブロイの業績全てが否定をされたわけではありません。

20世紀の量子力学の誕生の過程は、たとえて言うと「真理への裏口からの侵入」でした。決定論や還元論的な実在論に基づいて、間違った紆余曲折の急峻な崖路を選んでしまった過程でした。現在では正面玄関入り口からの量子力学入門が可能となっています。それは「情報理論としての量子力学」という正統な理解に沿った順路です。下記の教科書は、その正面玄関入り口からの入門書となっております。