
経済学とゲージ場の理論 (4/4)
【要約】
為替相場とゲージ場の理論の関係について 第4回(全4回)
※ noteのエディタに追加された新機能を使ってみるのも目的
まえおき
本記事は以下の記事の続きです:
参考文献について:本記事はRef.[1]を元に書いています。Ref.[2][3]はRef.[1]がベースにしている論文です。Ref.[4]は為替相場のゲージ理論からBlack-Scholes方程式を導く論文です。
格子ゲージ理論とは
量子的なゲージ理論を解析的に扱うのは大変です。そこで近似として、結合定数が小さいときに有効な摂動論を使うのが一般的です。量子電磁気学ではこの近似が大変良いのですが、しかし、どんな理論でもそうであるとは限りません。例えば強い力を記述するゲージ理論である量子色力学(QCD)の場合、興味あるエネルギー領域では強結合になります。そのため解析計算が非常に行いにくいです。
強結合領域で重要な計算手法が格子ゲージ理論です。格子ゲージ理論はその名のとおり、粒子の場を格子状に離散化して経路積分を行う方法です。摂動論に依らずに場の量子論の計算を行えます。解析的にも重要ですが、近年では特に数値計算において大変重要な手法です。大規模な数値計算がこれにより行われています。強い相互作用の物理量が次々に計算され、実験で得られている結果の再現、および新たな現象の予言もなされています。
実は今まで議論してきた為替取引のゲージ理論は、格子ゲージ理論の方が直接の対応を持ちます。
為替取引において、$${R}$$は為替相場、$${M}$$は裁定取引の利益率でした。しかしなぜか

のように、$${R}$$や$${M}$$のlogをとった変数を作りました。
これはMaxwell方程式のゲージ理論と対応をつけたかったからです。実際に自然界で実現しているMaxwell理論は、$${R}$$や$${M}$$ではなく$${A}$$や$${F}$$で書かれています。
しかし、物理学でも$${R, M}$$に対応する変数で計算する場合があります。それが格子ゲージ理論です。数学的な言い方をすると、$${A}$$や$${F}$$がいわゆるリー環の元であるのに対し、$${R}$$や$${M}$$はリー群の元です。環の元はその生成子の線形結合で書けます。そして生成子同士の交換関係が分かると様々な計算が実行できます。$${A,F}$$は解析計算、特に摂動論の計算にはよいのですが、経路積分を数値的に実行する際にはあまり良い表現ではありません。むしろ変数を$${R }$$や$${M }$$に変更するほうが計算しやすいです。$${A }$$や$${F }$$の表現だと、それらを変数でパラメトライズしたとき、無限大まで考慮しなければならなくなります。一方、$${R,M}$$で理論を展開する形式は「コンパクトな形式」と呼ばれ、それらをパラメトライズする際の変数が有限の領域に収まります。これは数値計算では大変重宝します。(※「為替取引の格子ゲージ理論」の場合、コンパクトな形式にはなりません。これは、為替取引の対称性が、Maxwell理論に存在する(複素空間の)回転不変性ではなく、スケール不変性だからです)
もうひとつ、格子ゲージ理論の利点として、ゲージ固定を行う必要がないことが挙げられます。U(1)ゲージ理論の摂動論では光子の伝播関数という量を扱う必要があるのですが、この量を得るには、ゲージ固定という、光子の運動の不定性を取り除く作業を行わないといけません(これはゲージ理論が特異系であることに由来するんだと思います)。最終的にはゲージ不変量(=ゲージ変換で不変な量。ゲージ固定に依存しない量。為替相場で言えば裁定取引のような量)のみ計算するとしても、ゲージ固定せずには計算できないのです。しかし格子上では、ゲージ不変な量を計算するなら、ゲージ固定をする必要がありません。これは格子ゲージ理論のひとつの重要な利点です。
U(1)の格子ゲージ理論
実際に格子ゲージ理論を見ていきましょう。
以前と同じように、各国を格子上に配置します。$${d+1}$$次元の場所を

で指定します。そして
$$
\begin{align*}
&\hat\mu=(0,0,\ldots,a,0,0,\ldots,0)\\&ただしaが存在するのは\muの位置\\{}\\&たとえばd=3,\mu=0なら\\&\hspace{1cm}\hat 0=(a,0,0,0)\\ &\mu=3なら\\ &\hspace{1cm}\hat 3=(0,0,0,a)
\end{align*}
$$
という量を用意します。そして
$$
\begin{align*}
&R_\mu(n): nに存在する国の通貨に対する\\ &\hspace{1.2cm}n+\hat\muに存在する国の通貨の為替相場\\&M_{\mu\nu}: n\Rightarrow n+\hat\mu\Rightarrow n+\hat\mu+\hat\nu\Rightarrow n+\hat\nu\Rightarrow n\\ &\hspace{0.9cm}のループにおける裁定取引による利益率
\end{align*}
$$
とします。$${M}$$は$${R}$$で以下のように書けます:
$$
\begin{align*}
M_{\mu\nu}(n)&=R_\mu(n)R_\nu(n+\hat\mu)R^{-1}_\mu(n+\hat\nu)R^{-1}_\nu(n),\\R^{-1}_\mu(n)&=1/R_\mu (n).
\end{align*}
$$
ここで、運動を決めるラグランジアンという量を、格子上で書きましょう。
力学の形式に「ラグランジュ形式」というものがあります。ラグランジュ形式では運動はラグランジアン(および作用)という量で定まります。この形式では、運動を決める原理は「微小変分に対し作用が極小になるような時間発展が実現する」というものになります。理屈は省きますが、ラグランジアンがある場$${\phi}$$で

と書かれるとき($${i}$$は粒子の種類)、上記原理により、Euler-Lagrange方程式

が$${i}$$ごとに成立します。
U(1)ゲージ理論では、ラグランジアンは

と書かれます(荷電粒子によるカレントは存在しないとする)。$${F}$$は「場の強さ(field strength)」と呼ばれます。このラグランジアンに対し、Euler-Lagrange方程式
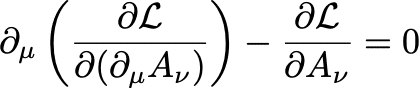
を計算すると
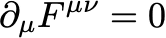
となります。これは前回話したMaxwell方程式です。確かにラグランジアンとEuler-Lagrange方程式が場の運動を決定しています。
上記のラグランジアンを、$${M}$$や$${R}$$から作り出す方法を考えます。前回までの議論から、$${M}$$は

と書けます。ここで$${a}$$の2乗が$${F}$$にかかっています。これは、Maxwell理論では$${F}$$の次元を無くすために必要なファクターです(記事末尾(注)参照)。
実はこのままだと、U(1)格子ゲージ理論とは違う点があります。何が違うかというと、U(1)格子ゲージ理論では、対称性が為替の場合と違いU(1)であるため、Eq.(1)の肩に虚数単位iが存在するのです。ここから、肩に$${i}$$をかけ、U(1)ゲージ理論に移行します。そして$${M}$$を$${a}$$が小さい、すなわち連続極限に近いとしてテイラー展開します(記事末尾(注2)参照):

下式第3項は、$${\mu,\nu}$$に関して和をとれば、ラグランジアンの$${FF}$$の項と等しくなります。ただし最初の2項を消す必要があります。また$${a}$$の5乗以降の項は、$${a}$$が小さいとして無視します。最初の2項を消すには

という$${M}$$の組み合わせを作ればいいです。ここで†は複素共役を表します。あとは$${\mu\nu}$$で和をとれば、ラグランジアンが得られます:

ここで2行目では$${\mu\nu}$$の和がなくなり、$${M}$$の添字に$${P}$$がつき、和は$${P}$$なる変数で行われています。これは単に記号を変えただけなのですが、説明しておきます。$${M}$$は点$${n}$$における隣国の四角いループを表すのでした。点nにおけるループは6つあります。点$${n}$$から0→1, 0→2, 0→3, 1→2, 1→3, 2→3方向に進み、その平面内でループを作ったものが6つのループです。これをplaquetteと呼びます。フランス語で「小さな盾」の意味らしいです。この4つのplaquetteの和を「$${P}$$の和」で表しています。$${\mu\nu}$$での和はplaquette両回りの和をとることに対応しますが、$${P}$$の和では1つの回り方のみに制限しています。2行目の係数が1行目に対して2倍になるのはこのためです。
3次元でplaquetteを説明したのがFig.(1)です。$${n=(0,0,0)}$$から1-2=$${x}$$-$${y}$$平面 (赤), 1-3=$${x}$$-$${z}$$平面 (緑), 2-3=$${y}$$-$${z}$$平面(青)の3つのplaquetteが示されています。3次元ならこの3つのplaquetteの和が「$${P}$$の和」に対応します。

ラグランジアンを時空の足に関して和をとった(=連続極限では「積分した」)ものが作用と呼ばれる量で、以下のようになります:

ここで、最後の行の「$${P}$$の和」は、上記した「ある点$${n}$$における6つのplaquetteの和」および「$${n}$$の和」両方が考慮されていると思ってください。つまり「時空全体で可能な、1方向回りplaquetteすべての和」だと解釈します。また、$${M}$$は”為替相場”$${R}$$に依存することを示すため、顕わに$${R}$$を引数に書いています。
量子論に移行する
量子論というと難しく感じるかもしれません。しかし経路積分は偉大で、直感的に非常にわかりやすい計算法を与えてくれます。
場の量子論における経路積分では、なんらかのオペレータの量子力学的期待値を、可能なすべての$${R}$$の配位で平均することで計算します。平均をとるときの重みは$${\exp(-S)}$$で行います。期待値を求めたいオペレータを$${O(R)}$$とすると、この期待値$${\langle O(R)\rangle}$$は以下のように表されます:

ここで和の部分は可能な$${R}$$すべての配位の和を意味します。$${S[R]}$$と書いたのは、$${S}$$が$${R}$$の汎関数であることを顕わに表すためです。
上記の平均の式は、もともとMinkowski空間で定義されているものを、Euclid空間に解析接続した表式です。Minkowski空間では重みは$${\exp(iS)}$$のように複素位相なのですが、これをEuclid空間に解析接続すると、$${\exp(-S)}$$になります。このように格子ゲージ理論ではEuclid空間で計算を行います。そしてこの操作により、量子論的な平均が統計力学的平均になります。ただしハミルトニアンではなく作用が重みとなることに注意してください。
統計力学系では時間発展という概念がありません。そのかわり分布を仮定し、様々な配位に関して和をとることで物理量を求めます(記事末(注3)参照)。一方、Eq.(2)では、作用は4次元的な配位$${R}$$に依存します。$${R}$$は空間だけでなく時間にも依存しており、時間的履歴まで含め可能な限りの$${R}$$を作り和をとります。ただしEuclid空間なので、時間も「空間的」な軸になります。これが量子力学的な期待値の計算に対応します。このことから、
ある次元での量子力学は、それより1次元高いEuclid空間での統計力学系により記述される
という示唆的(?)な対応が得られます。
まあでも、とにかくこれを計算すればよいです。
数値計算の困難さ: Importance sampling
しかし格子ゲージ理論の数値計算はなかなかに大変です。様々な困難が存在します。ここではそのうちの1つの困難とその解決法に関して軽く触れます。
U(1)の場合の格子ゲージ理論の計算をどう実行するか考えてみましょう。このとき$${R}$$は

と表せます。そして各$${n, \mu}$$に対して$${\theta}$$をランダムに$${(0,2\pi)}$$の区間で発生させ重みを計算し期待値をとれば、それで計算ができると思うかもしれません。これはいわゆるモンテカルロ法です。しかし実はそれではなかなかうまくいきません。なぜなら、発生させた殆どの配位で、重み$${\exp(-S[R])}$$が非常に小さくなるからです。同じことですが、$${\exp(-S[R]) }$$を大きくするような重要な配位が、ランダムな$${\theta }$$からはほとんど生み出せないのです。そこで重要な配位を生成するimportance samplingということをしなければなりません。importance samplingでは、確率$${\exp(-S[R])}$$で配位$${R}$$を生成させます。そうすれば当然ですが$${\exp(-S[R])}$$を大きくする配位がたくさん生成されます。配位にはすでに発生確率に重みが考慮されているので、これらを用いてオペレータの”重み1”の平均(つまりはふつうの平均)をとれば計算が完了します。
この困難の例えとして次のようなことを考えます。ダーツの矢を地球表面に一様ランダムに投げます。ダーツの的を南極点に置きましょう。100本なげて何点とれるか?と聞かれたら、だれもが0点と答えるでしょう。地球全体の面積に対し、ダーツの的など、ちっぽけもいいところです。しかしもし、ダーツの的の点数に比例した確率で、その点数の場所に矢が刺さるとしたらどうでしょう。的の外では0点だとしたら、そもそも的以外にはささりません。高得点の場所ほど刺さりやすいです。獲得点数は全く違うことでしょう。前者がナイーブなモンテカルロ、後者がimportance samplingです。
importance samplingはチートに見えるのですが、実際可能です。その手法は幾つかあります。熱浴法、メトロポリス法、確率過程的手法、分子動力学的手法など、長年の研究の中で最適な方法が試されてきました。現在の主流は、確率過程量子化と分子動力学的手法を組み合わせたhybrid Monte-Carloです。これを説明するのは今回の記事のシリーズの目的からは逸脱するのでやめておきます。
格子ゲージ理論の困難はほかにもたくさんあります。たとえば
フェルミオンを扱うときにダブラーというfakeな自由度をいかに消すか
動的フェルミオンをいかに効率よく計算に取り入れるか
カイラル対称性をいかに格子上で実現するか
超対称性をいかに格子上で実現するか
有限密度系や、強い相互作用でのCP問題における符号問題をいかに克服するか
大規模数値計算の際いかに効率よく計算を行うか
などなど、が挙げられます。
ちょっと尻切れトンボ感はありますが、主題の経済学とゲージ場の理論の関係に関してはある程度話せたので、このへんでおしまいにします。
4回の記事全体のまとめと展望
経済学とゲージ理論との対応を見てきました。まとめると以下のようになります:
デノミは各国通貨の基準の変更である。これにより所有する金額の数字が変化しても、価値は変化していない
為替裁定取引では、実際に取引を行った場合、実際に価値を増やしたことになる
為替相場$${R}$$はデノミに依存する。デノミによる為替相場の変化は価値の変化とは無関係である
裁定取引の利益率$${M}$$はデノミに依存しない。意味がある
ゲージ理論の言葉で言えば、$${R}$$はゲージ場(数学では接続)、$${M}$$は場の強さ(数学では曲率)と関係する
裁定取引のゲージ理論は格子ゲージ理論と直接の関係をもつ
為替裁定取引は、ある時刻の為替相場に従って行うことに注意してください。違う時刻で取引により自身の所有する金額が額面上変化した場合、単位あたりの通貨の価値自体の変化による影響が入る可能性があります。しかし裁定取引は特定の時刻での話なので、額面が増えるということは、紛うことなく純粋に「価値」を増やすことになります。なんだか不思議です。
経済学とゲージ理論との対応はもうちょっと先があるようです。デリバティブに現れるBlack–Scholesの方程式を、今まで展開してきた為替相場のゲージ理論から導くこともできるようです(Ref.[4])。これはそれほど不思議なことではないように感じます。Black-Scholes方程式は確率微分方程式です。上記したように、格子ゲージ理論はそもそも確率微分方程式を用いた確率過程量子化と密接な関連があります。どれだけ現実と対応するかは別として、形式的には同じような微分方程式に従っても不思議ではありません。蛇足ですが、今年2021年にノーベル物理学賞を受賞されたG.Parisiさんは、場の量子論における確率過程量子化の開祖です。また後日このあたりのことに関して書きたい気もしますが、今シリーズに関してはとりあえずここで筆を置きたいと思います。
記事を読んでくださった稀有な方々に感謝致します。
■
(注)ここでは自然単位系という、素粒子物理でよく使われる単位系を使用しています。この単位系では、あらゆる次元を長さの次元で表すことができます。$${F}$$は長さの次元で−2であるため、長さの次元2をもつ$${a}$$の2乗をかけると次元なしになります。expやlogの引数となる数は次元なしにならなければいけないことに注意してください。そうでないと、これらの関数をテイラー展開したとき、違う次元の量の和をとることになります。
(注2)考えてみると、$${M}$$のlogをとってやれば、連続極限か否かに依存せず$${F}$$が正確に求まります。なぜそうしないのでしょうか。それは、U(1)のような「可換ゲージ理論」ではなく、SU(2)やSU(3)のような「非可換ゲージ理論」の場合を考えるとわかります。非可換ゲージ理論の場合、$${A}$$や$${F}$$は行列になります。よって$${R=\exp(iA)}$$や$${M=\exp(iF)}$$の左辺も右辺も行列です。行列のexpはテイラー展開で定義されるのですが、それはおいておきます。とにかくRやMはSU(2)なら2x2、SU(3)なら3x3の複素数の要素をもつ正方行列です。そして問題は$${\log(R)}$$や$${\log(M)}$$を計算するのが大変だということです。$$\log(R), \log(M)}$$は$${R}$$や$${M}$$を対角化しないと求まりません。格子上には格子点ごとに$${R,M}$$が存在し、それらのlogをいちいち計算するのはかなり計算コストがかかります。他の場所でどうせ$${a}$$の展開を用いているのだから、logの計算をがんばるだけムダです。よって展開してO($${a}$$)で一致するようにすればOKと考えます。
(注3)これは多粒子系の時間発展において、配位が相空間をくまなく全体に動くことで統計分布が実現されるという性質が背後にあるかと思います。分子動力学により統計平均を計算する手法は、これに基づきます。
参考文献
[1] J. Schwichtenberg, “Demystifying Gauge Symmetry,” arXiv:1901.10420v1 (2019).
[2] K. Ilinski, “Physics of Finance,” hep-th/9710148 (1997).
[3] K. Young, “Foreign exchange market as a lattice gauge theory,” American Journal of Physics 67, 862 (1999).
[4] K.Llinski, G.Kalinin, “Black-Scholes equation from Gauge Theory of Arbitrage,” hep-th/9712034 (1997).
