
経済学とゲージ場の理論 (3/4)
【要約】
為替相場とゲージ場の理論の関係について 第3回(全4回)
※ noteのエディタに追加された新機能を使ってみるのも目的
まえがき
本記事は前回の記事:
の続きです。
前回の復習
前回、格子状の世界における為替取引を考え、その連続極限をとりました。その結果以下のような結論を得ました:

今回は主に物理の観点からゲージ理論についてお話します。
参考文献は前回と同じです。今回もRef.[1]を主に参照しています。Ref.[2][3]は本記事を読むのに有用な参考文献です。
連続極限における局所デノミによる不変性
物理に入る前に、「為替取引の連続極限」におけるデノミの影響を調べておきましょう。
今まで話してきたように、$${A}$$はデノミで変化し、$${F}$$はデノミの影響を受けません。この事実を、今度は連続極限で確かめます。
いま、各国が$${Ω(x)}$$倍のデノミを行ったとしましょう。すると

となります。$${Ω(x)}$$を
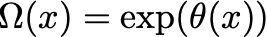
と書くことにします。$${R}$$の変換性を$${A}$$と$${θ}$$で書くと

となります。すなわち各国の$${Ω(x)}$$倍のデノミにより

と変換します。この変換が$${F}$$に影響を与えないのは簡単にわかります:
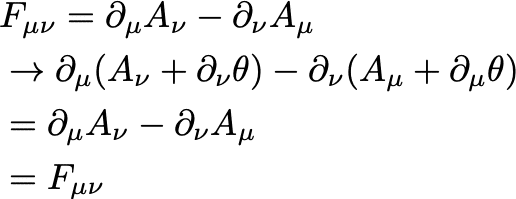
次に物理サイドのゲージ理論を見ていきます。
Maxwell方程式
電磁気学では電場・磁場が登場します。電気による力・磁気による力はこれら電磁・磁場が伝達します。この電場・磁場が時間と共にどう変化するか、及び電荷がどう動くかを知ることが、電磁気学において必要な情報のすべてです。
電磁場のダイナミクスを記述する方程式がマックスウェル方程式です。それは以下のような方程式群です:
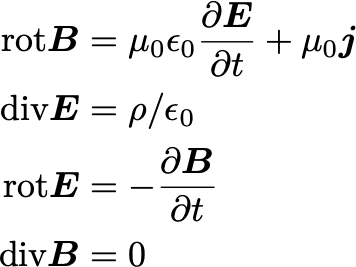
太字は空間3次元のベクトル量です。$${\boldsymbol E}$$は電場、$${\boldsymbol B}$$は磁場と呼ばれ、それぞれ電気の力、磁気の力を伝える場です。場というのは、空間と時間の各点で定義される量のことです。太字の記号は、空間3次元のベクトルを表します。$${{\partial}/{\partial t}}$$は時間による偏微分、$${\boldsymbol j}$$は電流です。$${\rho}$$は電荷の密度です。$${\epsilon_0, \mu_0}$$は真空の誘電率および真空の透磁率と呼ばれますが、単なる定数なのであまり気にしないでください。
rot、div、gradは任意のベクトル$${\boldsymbol V}$$とスカラー関数(ふつうの関数)$${\psi}$$に対して

のように作用する作用素です。rotはベクトルに作用しベクトルを返す演算子、divはベクトルに作用しスカラー関数を返す演算子、gradはスカラー数に作用しベクトルを返す演算子であることに注意してください。
Maxwell方程式Eq.(1)にはそれぞれ意味があり、上から
電磁誘導の法則(磁場の変化が電場を生む)
アンペールの法則、ビオ・サバールの法則(電場の変化および電流が磁場を生む)
ガウスの法則(電荷密度が電場を生む)
点磁荷は存在しない
を表します。
実はこの方程式群、場のとり方を変えると非常にシンプルに書き直すことができます。まずベクトルポテンシャル$${\boldsymbol A}$$とスカラーポテンシャル$${\phi}$$という場を用意し、磁場と電場を以下のように表します:

「ポテンシャル」と呼ばれる理由は、$${\phi}$$や$${\boldsymbol A}$$の時間・空間微分からB, Eが得られることに由来します。
Maxwell方程式を$${\phi,\boldsymbol{A}}$$で書き直そうとすると、面白いことに気付きます。次の

より、Eq.(1)の下2つの式が恒等的に成立する(=どんな$${\boldsymbol A}$$と$${\phi}$$でも成立する)ことがわかります。すなわち、Maxwell方程式のうち2つは、Eq.(2)の場の取り直し方に内在する恒等式に置き換えられたのです。
一方Eq.(1)の上2つの式は恒等式にはなりませんが、記法を整えると大変シンプルに書けます。以下の量を定義します:
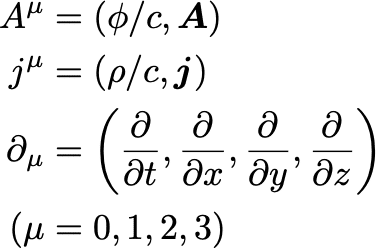
$${\mu=0}$$は時間成分を、$${\mu=1,2,3}$$はそれぞれ空間の$${x,y,z}$$成分を表します。また$${c}$$は光の速度です。これらより、Eq.(1)の1・2番目の式は、以下のように統一的に書けます:
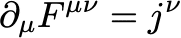
ここでFは以下のように定義されます:

$${F}$$は$${\boldsymbol E,\boldsymbol B}$$で書けます。その関係は以下のようになります:

Eq.(3)の左辺には$${\mu}$$が2回現れます。このとき、$${\mu}$$に関して和をとるという、いわゆるEinsteinの規約を使っていることに注意してください。すなわちEq.(3)の左辺は

のことです。Eq.(1)の一番上の式がEq.(3)の$${\nu=1,2,3}$$に対応し($${\epsilon_0,\mu_0}$$はずれても気にしないでください)、Eq.(1)の2番目の式はEq.(3)の$${\nu=0}$$に対応します。
さて、ゲージ変換と呼ばれる以下の変換

による各量の変化を考えます。$${F}$$はこの変換で不変です:

ということは、$${\boldsymbol j}$$が存在しないMaxwell方程式

もまたゲージ変換で不変(正確には共変)です。実はjもゲージ不変なので、$${\boldsymbol j}$$が存在するMaxwell方程式Eq.(3)も不変です(これにはjの構成を知る必要があります。とりあえず信じてください)。
ゲージ変換による$${F}$$の不変性は、磁場$${\boldsymbol B}$$と電場$${\boldsymbol E}$$が次の変換

に対し以下のように不変であることと等価です:

為替取引とMaxwell理論の比較
ここまで見てきてもうお気づきかと思いますが、為替取引に登場した$${A, F}$$と、Maxwell理論に登場する$${A, F}$$は似通っています。対応を図にすると以下のような感じになります:

Maxwell方程式におけるゲージ変換は、ポテンシャルの基準を時空の各点で変えてよいことを表します。これは為替取引の方だと各国のデノミに対応します。また「連続極限における局所デノミによる不変性」と「Maxwell方程式」の最後のほうで示したように、ゲージ変換でもデノミでも$${A,F}$$の変換性は同じです。(記事末尾(注)参照)
ゲージ理論の核心は何か
実は、為替に限らず何らかの量を違う単位で測る国が存在すれば、今までと同じ議論ができます。
例えば各国で長さの単位が違う状況を考えましょう。$${a}$$国ではLng($${a}$$)という単位を使って長さを測っています。単位の換算係数$${\rm R(ij)}$$を、

とします。ここで、ある国$${\rm ij}$$が長さの単位の変更をしたとします:

これにより$${\rm R(ij)}$$は

と変換します。$${\rm ij}$$が隣同士の場合のみ考え$${\rm R}$$のlogをとったものがゲージ場です。為替の場合と同じです。また

がこの変換で不変なのも為替と同じです。これのlogが$${F}$$です。
この例をみると、ゲージ理論はそもそも「各国(各時空点)において、測る単位が任意な何か」を考えればいつでも成立しそうな気がします。
実はここまでの話なら、数学で言うところの「Riemann幾何学」で為替の話を展開した、というのがふさわしいです(正確にはファイバーバンドル)。Riemann幾何学とは「曲がりねじれた空間」を扱う幾何学です。この理論では、Riemann多様体という、数学的によく定義された空間を扱います。平面とか、地球上のような球面がその例です。
この理論のひとつの主題は、その多様体が曲がっていることをどう記述するかにあります。Riemann幾何学において、曲率(曲がり具合)は、次のように測ります:「多様体上にベクトルを立て、それをある経路に沿って「平行移動」し、ぐるっと一周して戻ってきたとき、もとのベクトルとどれだけ異なるかを計算する」。並行移動は接続(今の場合ゲージ場)により定められます。接続が違えば、並行移動も変化し、曲率も変化します。曲率がノンゼロなら、多様体は曲がっていると見なされます。為替の場合も同じです。為替取引を次々に行い、元の通貨に戻したとき、$${R}$$が1からずれる(=$${F}$$が0からずれる)なら裁定取引でした。リーマン幾何学と対応させるなら、裁定取引=「価値空間の曲がり具合」です。
Riemann幾何学では、多様体を記述するためのアプリオリな座標は存在しません。それならどんな座標で記述しようと、曲がり方という実際に意味をもつ量は不変でなければなりません。裁定取引が各国のデノミに依存しないのは、Riemann幾何学において座標のとり方に曲率が依存しないことに対応します。
立ち返り、もう一度上で提示した疑問を繰り返します。「各国(各時空点)において、測る単位が任意な何か」を考えればいつでも現れるゲージ理論の、何が重要で面白いのでしょうか。
答えは、ゲージ場が動的に、時々刻々と変化することにあります。
さきほどの長さの単位の違いに関する「ゲージ理論」ですが、よくよく考えると、長さの基準を変えること以外、ゲージ場が変化することはありません。例えばメートル原器(今は使われていませんが)と各国の$${\rm Lng(i)}$$の基準器があれば、それでR(ij)は全て決まります。基準の変更をしなければ$${\rm R(ij)}$$が変化することはありません。さらに言えば、$${\rm M(ijkl)}$$はいつでも1です。$${F}$$で言えば0です。$${F}$$が0でない場合は、単純に何か間違っているだけです。
ところが為替取引は違います。そもそも「価値」という、とても漠然とした対象に座標を入れ数値にしたのが世界の為替相場です。様々な人々の思惑によるお金・物資の取引等で実に様々に「価値」は変化します。そのため時に$${F}$$も0からずれます。この裁定取引を利用して儲けようとして実際に取引が行われると、その不均衡は解消へ向かいます。しかしまた、なんらかのきっかけで$${F}$$が0から変化します。このような複雑で豊かなダイナミクスこそが、ゲージ理論の豊かさです。
素粒子論でも同じです。ゲージ場は、電磁気学なら電荷が動くことで、弱い力や強い力では、それらに対応するチャージが運動することで、重力なら質量やエネルギーが流れることで、ゲージ場が変化します。変化するのですが、場には元に戻ろうとする性質があるので、場はいつまでも大きくなることはなく(ときに不安定性により急激に大きくなることもありますが)、揺れることになります。それぞれの理論の$${F}$$に当たる量もダイナミカルに変化し、実際に観測にかかります。近年観測に成功した重力波は、重い天体の運動により重力場に歪みが生じて波となり、それが遥か遠くの地球まで届いたものです。
おそらく為替相場にも、似たような現象が起こるのではないでしょうか。あまり良い例ではないですが、地球上のどこかで災害が起きれば、その影響はまずその周辺の為替に影響を及ぼし、それがさざなみのように世界に伝わるでしょう。為替相場もまさに波のような性質をもつことがあるんじゃないかと思います(いや実は調べてもないのですが…)。
電磁場の場合、運動を記述するのはMaxwell方程式でした。ゲージ場で言うと
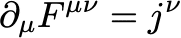
でした。一方為替相場の場合、jはお金の流れや売り買いする物の流れになるかと思います。この「運動方程式」が為替相場で成立しているかは実はよくわからないのですが、$${\boldsymbol j}$$が為替相場に影響を与えるのは確かなので、似たような式が成立していてもおかしくないと思います(よくわからんです)。
まとめ&次回予告
今回は為替相場とゲージ理論との対応を説明しました。
次回は為替相場と格子ゲージ理論との対応などを見ようと思います。
■
(注)実はゲージ変換に関し、為替とMaxwell方程式では「対称性」が異なります。為替のほうはお金の基準の変換で、これはいわゆる「スケール変換」です。$${\rm GL^+(1,R)}$$と呼ばれる群の元による変換です。一方Maxwell方程式のほうは回転の対称性で、U(1)と呼ばれる群の元で変換が行われます。
参考文献
[1] J. Schwichtenberg, “Demystifying Gauge Symmetry,” arXiv:1901.10420v1 (2019).
[2] K. Ilinski, “Physics of Finance,” hep-th/9710148 (1997).
[3] K. Young, “Foreign exchange market as a lattice gauge theory,” American Journal of Physics 67, 862 (1999).
