
Piece CHECK(2024-52) 2024年良問BEST15(3位) 積分法・面積
いつもご覧いただきまして、ありがとうございます。KATSUYAです。
【最新巻】計算練習帳『計算0.9』販売開始!!
こちらは、『Principle Piece』シリーズ一覧のページです(全分野そろってます)
1つの問題から、多くの問題が出来るようになるための考え方・手法、すなわち
原則(Principle Piece)
を出来る限り分かりやすく、そして詳しく言葉に落とし込んだ数学の問題集です。解答の詳しさはもちろんですが
「なぜそのような解答になるのか」が分かる
ことを、とにかく意識した参考書になります。
単元自体を未習の方も、本シリーズで最初から体系的に高校数学を学べます。そして、学習後の到達レベルは「難関大入試合格最低点レベル」です!
今回の問題
YouTube動画をUPしました。今回は2024年良問BESTシリーズの第3位の問題です。
神戸大学から、数IIIの積分法の問題です。
思考時間は約10分弱、目標解答時間はそこから約15分です。
解説・原則など
こちらも参照してください。(第5問です)
(1)は典型的な置換積分ですが、(2)は適度に発想も必要で差がつく問題でしょう。設定はシンプルですがいい問題だと思います。有名なtanの逆三角関数の問題で、神戸大はこの関数結構好きな印象(2012年にも出題)。
(1)はもちろんこちらの原則です。問題からも丸わかりですね。
$${\bm{\displaystyle \frac{1}{x^2+a^2}}}$$ は$${\bm{x=\tan \theta }}$$ とおく
(2)は、この関数がtanの逆三角関数であるという知識がないとちょっと思いつきにくいかも。f(x)+f(y)≦f(1)というのは、角度の条件が書かれているようなものです。x=tanα、y=tanβとするなら、α+β≦π/4ってことです。
これをx、yの条件に直すには、この式全体にもう一回tanをつけます。これが思いつくかどうかが勝負の分かれ目でしょう。
f(x)がtanの逆関数なので、tan(f(x))=xになります。f(x)の中からxやyを直接出すために、両辺にそのままtanをつけていることになります。
境界は1次の分数関数(双曲線の一部)なので、微分するまでもなく書いてOKでしょう。面積のための積分も簡単ですね。
1.解けた人・・・今後の勉強はじっくり演習をしましょう。
2.解けなくて原則を知っていた人・・・拙著『Principle Piece』シリーズで該当するページを熟読し(詳細が書いてあります)、入試演習用の問題集で思考時間を長くする演習をしましょう。
3.解けなくて原則も知らなかった人・・・原則集めからやる必要があります。拙著『Principle Piece』シリーズのような原則習得タイプの問題集で演習しましょう。
関連する拙著『Principle Piece』シリーズ
Principle Piece シリーズは、1つの問題から、多くの問題が出来るようになるための考え方・手法(原則:Principle)によって、「なぜその解法が思い浮かぶのか」「なぜ解答の1行目がそれになるのか」を意識して書き上げた参考書です。
大手ネットショップBASEでも、デジタルコンテンツとして販売しています。
解答

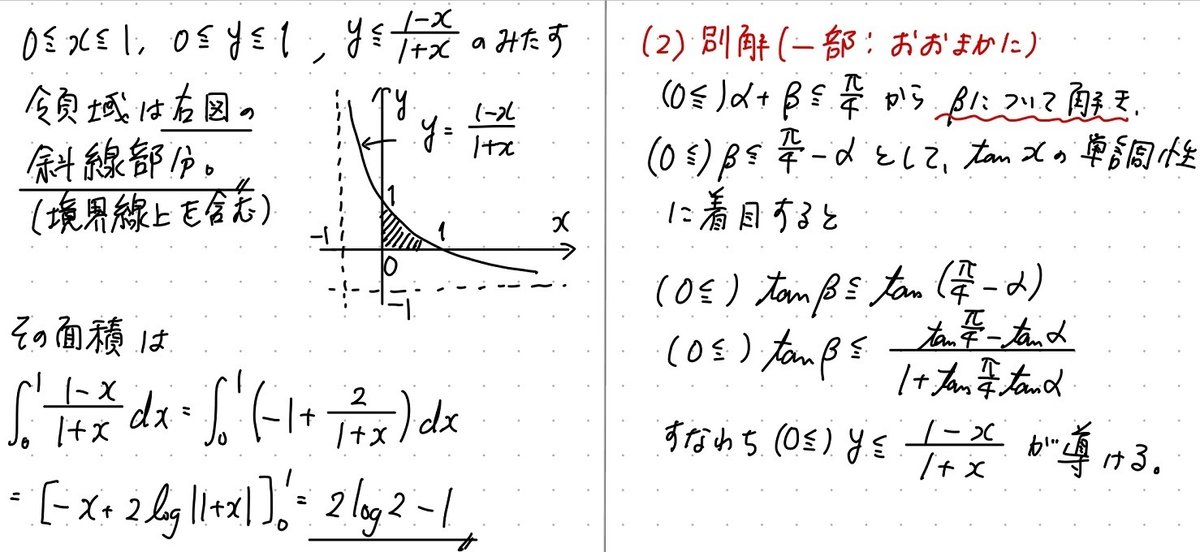
※ここより先には内容はございません。本記事に価値を感じていただけた方は、ポチっとしていただけると大変うれしいです。(もちろん、任意です)
ここから先は
¥ 100
Amazonギフトカード5,000円分が当たる
この記事が気に入ったらチップで応援してみませんか?
