PieceCHECK(2023-14) 2次関数と最大・最小

いつもご覧いただきまして、ありがとうございます。KATSUYAです。

YouTube動画をUPしました。今回は東京理科大学からで、条件つき最大・最小の問題です。

思考時間は5分、目標解答時間そこから約15分です。　

こちらの記事では、動画の中で紹介した解説(答え)を少し丁寧にした答案を、静止画像にて掲載しておきます。

解答

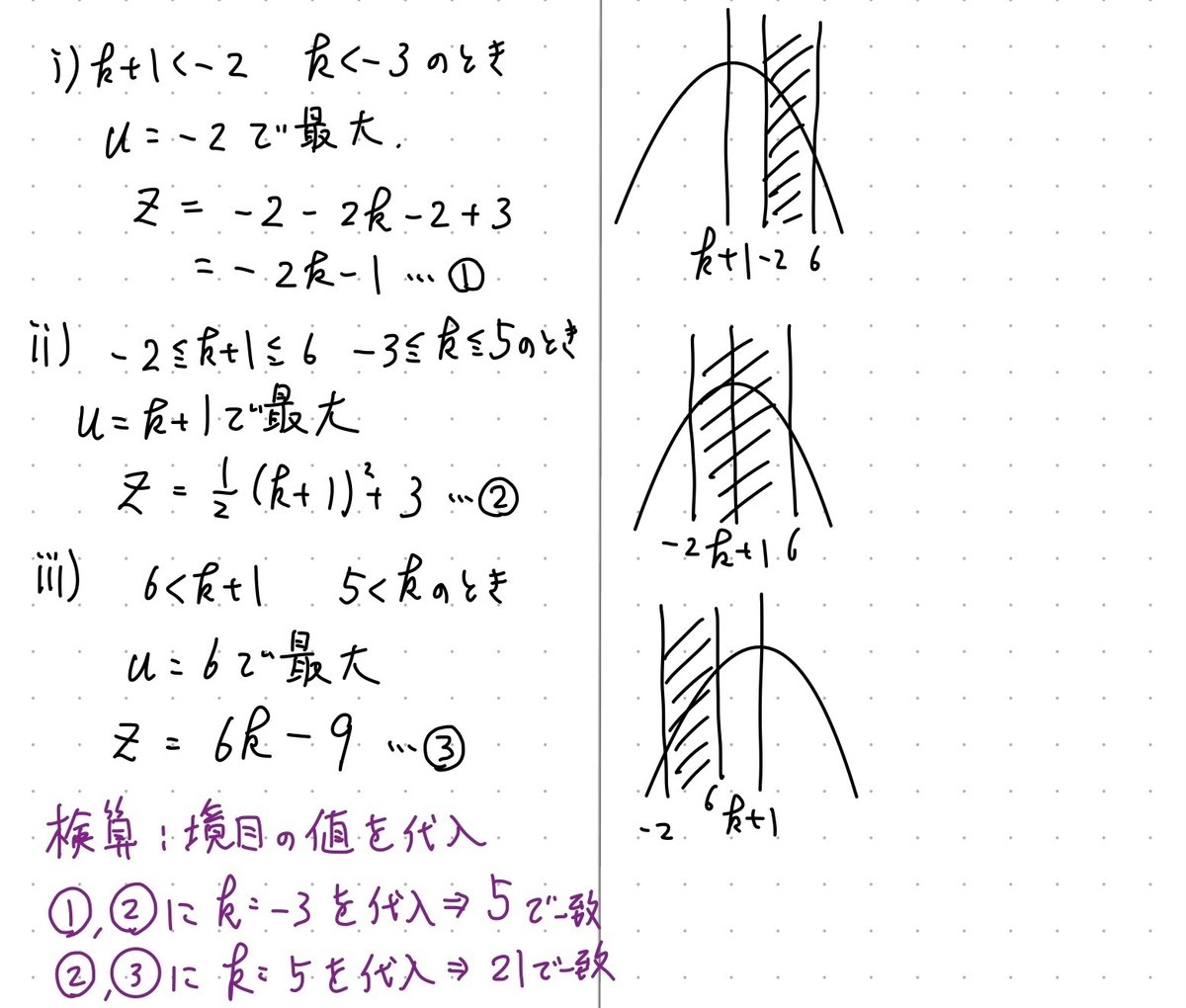
解説

題材としては2次関数の条件付き最大・最小の問題ですが、条件式から$${x=\cdots 、y=\cdots }$$。とするのは難しいタイプ。

まず気づきたいのは、条件式、そして最大値を求める式がともに$${\bm{x,y}}$$の対称式になっていることです。そこで、次の原則に従います。

対称式条件の場合は$${\bm{x+y,\ xy}}$$で表す→ただし「実数解条件」に注意

詳細は拙著シリーズ「数学Ⅰ～2次関数～」p.102を参照

和(=u)と積(=v)を主役に書き換えると、条件式は$${v=}$$にすることが出来ます。ここに暗黙の実数解条件が加わることに注意。2次方程式の判別式$${D\geqq 0}$$を忘れないようにしましょう。

これによりｕの範囲が出せて、最大値を求めたい式もｕだけになりました。定数ｋがあるので、後半のポイントは軸分けです。上に凸の放物線で最大値なので、3通りの場合分けですね。

軸が「入る」か「右ずれ」か「左ずれ」かで場合分け

詳細は拙著シリーズ「数学Ⅰ～2次関数～」p.31を参照

場合分けの問題はどうしてもミスが増えますので、検算をしましょう。場合分けの境目で値が一致していることを確認するだけでも、ケアレスミスをする確率が大きく下がります。

拙著シリーズ「数学Ⅰ～2次関数～」でも、場合分け関連の問題はしつこいぐらいに検算の確認の仕方を入れています。

１．解けた人・・・今後の勉強はじっくり演習をしましょう。

２．解けなくて原則を知っていた人・・・拙著『Principle Piece』シリーズで該当するページを熟読し(詳細が書いてあります)、入試演習用の問題集で思考時間を長くする演習をしましょう。

３．解けなくて原則も知らなかった人・・・原則集めからやる必要があります。拙著『Principle Piece』シリーズのような原則習得タイプの問題集で演習しましょう。

Piece CHECKシリーズは、出来あがった答案からは見えない部分を解説していくことで、「なぜそうやって解くのか」「いったいどこからそんな答案が生まれるのか」が分かることを意識して書き上げた参考書です。

関連する拙著『Principle Piece』シリーズ

大手ネットショップBASEでも、デジタルコンテンツとして販売しています。

principle powered by BASE

※ここより先には内容はございません。本記事に価値を感じていただけた方は、ポチっとしていただけると大変うれしいです。(もちろん、任意です)