
算数の時間 | 分数を理解しよう!
(1)算数・数学嫌いの始まりは「分数」
数学に苦手意識をもつ人は多い。いつ頃からスキ・嫌いがハッキリし始めるのか?、と考えてみると、小学生🎒で「分数」を習う頃かな、と思う。
ジブリ映画の「おもひでぽろぽろ」の中でも「分数」の話が出てくる。
算数・数学に苦手意識をもつのは、小学生・中学生に限ったことではない。以前にも「分数ができない大学生」という本が話題になったことがあった。
大学入試は多様化していて、経済学専攻にもかかわらず、数学を課さない大学も多い。また、現在の経済学の教科書をみると、従来の教科書よりも「数式」が極端に少ない、という印象がある。
もちろん、数式を用いなくても説明できることに敢えて数式を用いる必要はない。しかし、言葉で説明するよりも、1つの数式で表現したほうがスッキリする場合には、数式で表したほうがいいだろう。
(2)一応「分数」の「加減乗除」はできるけれども。
私自身は、小学生で習う分数の加減乗除の計算はできる。しかし、初めて分数を学ぶ小学生に理解できるような説明ができるかというと、自信がない。理屈を考えることなく、「機械的に」計算しているに過ぎない。
そこで、「小学生に分数を教えるとしたら?」という想定で、「分数の計算」(とりあえず「足し算」のみ)について考えてみたい。
(3)分数の足し算について。
たとえば、
( 1/2 ) + ( 2/3 ) を考えてみよう。
機械的に計算すれば、分母が2と3だから、6で「通分」して、分子を足し算すればよいから
( 3/6 ) + ( 4/6 ) = 7/6
答えは6分の7。
ただ答えを出すだけならばこれでよい。しかし、「何で通分するの?」「そもそも通分ってなーに?」と聞かれたら、答えに窮する人も多いのではないだろうか?
ここで、2つの「長方形」を使って、
1/2 (2分の1)と、2/3 (3分の2)を「見える化」してみよう。
次のような、タテ2cm、ヨコ3cmの長方形を準備する。

タテ2cm,ヨコ3cmの
長方形
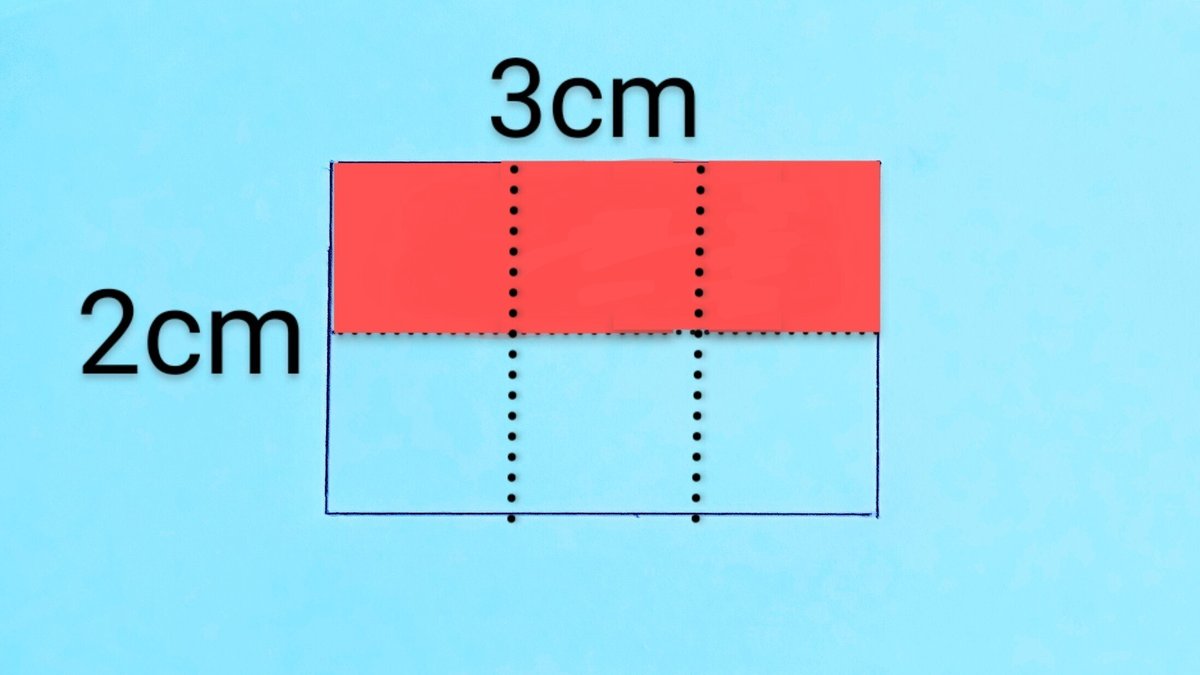
すると、1/2 (2分の1)は、全体を2等分したときの「1つ分」だから、次のように表せる。

赤🟥は長方形の面積の
「2分の1」
今、長方形をヨコに2分割したが、今度はタテに3分割すると、3分の2は次のように表せる。

青🟦は長方形の面積の
「3分の2」
1/2 + 2/3 は「赤い部分」と「青い部分」の足し算である。
ここで、タテの線と、ヨコの線の分け方は異なるので、図②と図③にそれぞれ、「タテの等分線」と「ヨコの等分線」を書き加えると次のようになる。
「2分の1」は
全体を6等分したモノの
「3つ分」

「3分の2」は
全体を6等分したモノの
「4つ分」
「通分」するとは、長方形のタテとヨコの長さの単位を揃えて、同じ面積に分けることに他ならない。
赤は6等分したもの「3つ分」、青は6等分したものの「4つ分」だから、両者を足し算すると6等分したものの「7つ分」。
よって
( 1/2 ) + ( 2/3 ) = 7/6
まとめ
掛け算、割り算についても、長方形を図示すれば同様に考えることができる(入力が面倒なのでサボる)。興味のある方は、ご自身でやってみると面白いかもしれない。
数学が得意だ!、と思っている人の中にも、機械的に計算しているだけで、意味は考えていない人も多いと思う。たまには、基本中の基本にたち戻ることは面白い。
いいなと思ったら応援しよう!

