2020年　東北大AO入試のあの難問

話題自体は去年の入試のものだが、東北大のAO入試でとある難問が出題された。それが次の問題である。

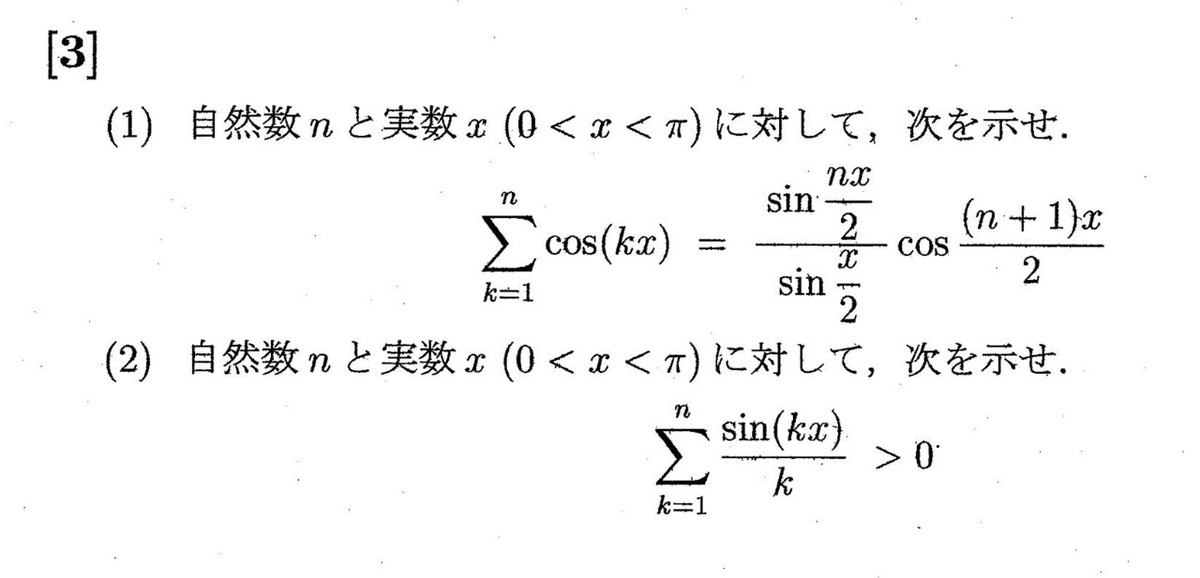
(1)はド・モアブルの定理から比較的容易に解決できるのだが、この(2)がかなりの難問であった。話題になっていたこともあり当時の自分も挑戦してみた。だが、解き切るのに数時間かかったし、そのうえスマートとは言えない超泥臭い力技(極値が正であることを示すために階差を2回とる)で解決したものであった。

さて、そんな問題もあったなぁと忘れかけていた先日のこと、ふとしたきっかけでこの問題を思い出すことになる。そのきっかけが以下のサイトの発見だ。

Inequality $\sum\limits_{1\le k\le n}\frac{\sin kx}{k}\ge 0$ (Fejer-Jackson)

このページの中に、(2)の証明がとてもきれいにまとめられている部分があったのだ。簡単に書き抜くと

・1 ≦ k ≦ m におけるsin(kx)/k の総和が0以下になるx (それをyとする) が存在するような最小のmの存在を仮定する
・1 ≦ k ≦ m における sin(kx)/k の総和を f(x) と定義する
・上の仮定から f(y) ≦ 0 = f(0) = f(π) が成り立つので、この f(x) には0以下の最小値が存在し、それを f(z) とおけば f(z) ≦ 0, f'(z) = 0 を満たす
・mが最小であることから、sin(mz)< 0 であり、sin(mz/2) ≠ 0, cos((m+1)z/2) ≠ 0 となる (これらが0になるとsin(mz)は0か0以上になることを示せば良い) ため、(1)より f'(z) = sin(mz/2)/sin(z/2) *cos((m+1)z/2) = 0 に矛盾する。

というものである。とてもスマートな証明で素直に感心してしまった。

出題サイドがどのような解答を想定していたのかはわからないが、高校数学の知識や範囲内で収められる解答としてはこれが現実的な解答なのかもしれない。

余談として、このサイトのタイトルにもあるように、(2)の不等式は「Fejer-Jackson inequality (フェイェール・ジャクソンの不等式)」という不等式で、この式の左辺はノコギリ波をフーリエ級数で表したものである。題材自体に応用面の広がりがある上、受験問題にも用いられるような数学的なおもしろみがある深い題材であると再認識させられる1問であった。