
【受験数学】不等式の定石~パスチャレ#021~
written by なも
皆さんこんにちは、なもです😃
withコロナの新しい生活様式に慣れるにはまだ時間がかかりそうですが、体調管理に気を付けて日々頑張っていきましょう。
さて、今朝の動画はもうチェック済み✅でしょうか?
動画には下の画像から飛べます!↴

【超難問】Twitterで高校教師から数学の問題が届きました。
https://youtu.be/MOVI7G4X79k
パスラボ未登録の方はぜひ見てみてくださいね👀
それでは今週のパスチャレを見ていきましょう❗今日は数学の問題です。

不等式の証明問題ですね〜
回答手順はパッと思いつきましたか??
まずは不等式の大小関係の示し方を思い出しましょう。
不等式 f(x)>g(x) の証明問題の定石は
1.f(x)-g(x)を因数分解する
2.f(x)-g(x)の最小値>0を示す
でしたね。
この問題ではa^3+b^3が目の付け所ですね、因数分解したくなってきませんか?(笑)
定石1に従って解答を作っていきましょう!
▽
▼
▽
▼
解答)
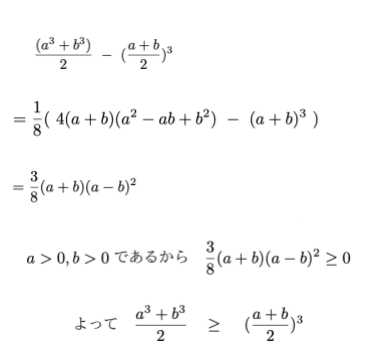
以上のように考えても良いですが、次はグラフという観点から調べてみましょう😉
「凸不等式」という言葉で知られる方法です。 関数の凸を利用すると、グラフで簡単に納得できますよ。
関数が上に凸か、下に凸かがわかると、ある2点と、その中点の関係を簡単に図示できますよね。今回の問題の場合、(a+b)/2をxとしたy=x^3のグラフが思い浮かべられたら解決までの道筋ができたも同然となります。
早速、図にしてみましょう。

今回ご紹介したように、数学の問題の解き方は、1つに限らないというケースが少なくありません。
自分が解きやすいと思う方法で、その都度解いていけばよいかとも思いますが、いろんな解き方に触れておくと応用力という強みに繋がる可能性が高まるかもしれません。
理解できたときの「なるほど!」を楽しみながらいろんな問題、解き方に触れられるといいですね。
おまけとして、不等式といえば存在感の強いあれ……
相加相乗平均の不等式 のおさらいもしておきましょう。
a+b≧2√ab ですね。
この不等式の証明は以下のようになります。
証明)両辺を二乗する:a^2+2ab+b^2≧4ab
移項すると (a-b)^2≧0
これは明らかに成立する。
等号成立の条件はa=b
この相加相乗平均の関係ですが、
1.証明する不等式の中に a と1/a のように、掛けたら文字が消えて定数となる組がある
2.aとbに該当する文字がそれぞれ正の数である
を満たしていたら出番となります。
更に、これを3変数に拡張すると、
a,b,c≧0のとき、
a+b+c≧3³√abc が成立します。等号成立条件はa=b=cです。
教科書レベルは超えていますが難関大受験者なら知っていて損はないものです。
a+b+c≧3³√abc を証明したいときは a^3+b^3+c^3≧3abc を示せばいいですね。
有名な因数分解公式
a^3+b^3+c^3-3abc=(a+b+c)(a^2+b^2+c^2-ab-bc-ca) と、
(a^2+b^2+c^2-ab-bc-ca)=1/2{(a-b)^2+(b-c)^2+(c-a)^2}
を利用して,
a,b,cが正の数のとき、
a^3+b^3+c^3-3abc=(a+b+c)(a^2+b^2+c^2-ab-bc-ca)
=(a+b+c)・1/2{(a-b)^2+(b-c)^2+(c-a)^2}≧0
よってa^3+b^3+c^3≧3abc が成立します。
a,b,cそれぞれに³√a,³√b,³√cを代入して相加相乗平均の不等式の完成です。
因数分解公式の導出は青チャートなどで確認しておきましょう☺
長くなりましたが最後までご覧いただきありがとうございました😘
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
お茶の水女子大学 理学部 1年 なも
生物が好きで理系という分類に属してはいるが、大学では倫理や哲学、心理学も学んでいて常に興味関心の赴くままに行動する。
猫・植物・おいしいもの・布団が好き。ちなみに猫は画面の中でしか飼っていない。
珈琲を嗜む優雅な生活に憧れている。
3DS以外にゲーム機を持っていないためあつもりブームに乗れず、せめてもと最近スマホでどうぶつの森ポケットキャンプを始めたが、まわりでやっている人がおらず孤独で虚無虚無プリンになっている。
