5次方程式の解の公式がない!？

解の公式がないとは、代数的に解けない（有限回の四則演算と有限回の累乗根だけでは表すことができない）ということです

解の公式について考えてみる

2次方程式の解を求めてみる

まず、2次方程式の解の求め方といえば平方完成…。
ここから解の公式を得ることができます
（因数分解は勘を働かせて解く方法なので除きます）
例えば、
　$${x^2-6x+3=0}$$
　$${x^2-6x=-3}$$
　$${x^2-6x+9=-3+9}$$
　$${(x-3)^2=6}$$
　$${x-3=\pm \sqrt{6}}$$
　$${x=3 \pm \sqrt{6}}$$

同じように
　$${ax^2+bx+c=0}$$
　$${\displaystyle x^2+\frac{b}{a}+\frac{c}{a}=0}$$

　$${\displaystyle x^2+2 \cdot \frac{b}{2a}x=-\frac{c}{a}}$$

　$${\displaystyle x^2+2 \cdot \frac{b}{2a}x +\left( \frac{b}{2a} \right)^2 =-\frac{c}{a}+\left( \frac{b}{2a} \right)^2}$$

　$${\displaystyle \left( x+\frac{b}{2a}\right)^2=\frac{b^2-4ac}{4a^2}}$$

　$${\displaystyle x+\frac{b}{2a}=\pm \frac{\sqrt{b^2-4ac}}{2a}}$$

　$${\displaystyle x=-\frac{b}{2a} \pm \frac{\sqrt{b^2-4ac}}{2a}}$$

別の方法で考えてみる

解 $${\alpha,\ \beta}$$ についてのある等式を考えてみます

　$${\displaystyle \alpha=\frac{\alpha+\beta}{2}+\frac{\alpha-\beta}{2}}$$

　$${\displaystyle \beta=\frac{\alpha+\beta}{2}+\frac{-\alpha+\beta}{2}}$$

ここで $${\alpha}$$ と $${\beta}$$ の置き換えについて考えてみます

(a) の $${\alpha}$$ を $${\alpha}$$ に $${\beta}$$ を $${\beta}$$ に置き換える場合は $${\alpha+\beta}$$ も $${\alpha-\beta}$$ も変化はありません

(b) の $${\alpha}$$ を $${\beta}$$ に $${\beta}$$ を $${\alpha}$$ に入れ替える場合、$${\alpha+\beta}$$ は $${\beta+\alpha}$$ となり式としては変化がありません
この性質を持つ式を対称式といいます

それに対して、$${\alpha-\beta}$$ は入れ替えると $${\beta-\alpha}$$ と符号が変わってしまいます
対称式とはいえません
しかし、2乗した $${(\alpha-\beta)^2}$$ は符号の変化が消えて、式として変化がなくなり対称式となります
また、重要な性質として対称式は基本対称式 $${\alpha+\beta}$$ と $${\alpha\beta}$$ で表すことができます

そして、2次方程式 $${ax^2+bx+c=0}$$ より$${\displaystyle x^2+\frac{b}{a}x+\frac{c}{a}=0}$$ と
$${(x-\alpha)(x-\beta)=0}$$ の左辺を展開したもの $${x^2-(\alpha+\beta)x+\alpha\beta=0}$$ の係数を比較すると

　$${\displaystyle \alpha+\beta=-\frac{b}{a}}$$
　$${\displaystyle \alpha\beta=\frac{c}{a}}$$

となるので（解と係数の関係）、
　$${(\alpha-\beta)^2=(\alpha+\beta)^2-4\alpha\beta}$$

　　　　　$${\displaystyle =\left(-\frac{b}{a} \right)^2-4\cdot \frac{c}{a}}$$

　　　　　$${\displaystyle =\frac{b^2-4ac}{a^2}}$$

よって、$${\alpha > \beta}$$ とすると
　$${\displaystyle \alpha-\beta=\frac{\sqrt{b^2-4ac}}{a}}$$

　$${\displaystyle \alpha= \frac{\alpha+\beta}{2}+\frac{\alpha-\beta}{2}}$$

　　$${\displaystyle =-\frac{b}{2a}+\frac{\sqrt{b^2-4ac}}{2a}}$$

　$${\displaystyle \beta= \frac{\alpha+\beta}{2}+\frac{-\alpha+\beta}{2}}$$

　　$${\displaystyle =-\frac{b}{2a}-\frac{\sqrt{b^2-4ac}}{2a}}$$

ここで $${\alpha-\beta}$$ を2次のラグランジュ・リゾルベントといいます
解を求めるための都合の良い分解式という意味です
ラグランジュという数学者が解の公式について考えていて出てきた式です

3次方程式の場合

3次方程式 $${ax^3+bx^2+cx+d=0}$$ の3つの解を $${\alpha,\ \beta,\ \gamma}$$ とします
また、$${x^3-1=0}$$ の複素解の1つを $${\omega}$$ とすると、$${\omega^2 +\omega+1=0}$$ という性質から

　$${\displaystyle \alpha=\frac{\alpha+\beta+\gamma}{3}+\frac{\alpha+\omega\beta+\omega^2 \gamma}{3}+\frac{\alpha+\omega^2 \beta+\omega\gamma}{3}}$$

　$${\displaystyle \beta=\frac{\alpha+\beta+\gamma}{3}+\frac{\omega^2 \alpha+\beta+\omega\gamma}{3}+\frac{\omega\alpha+\beta+\omega^2 \gamma}{3}}$$

　$${\displaystyle \gamma=\frac{\alpha+\beta+\gamma}{3}+\frac{\omega\alpha+\omega^2 \beta+\gamma}{3}+\frac{\omega^2 \alpha+\omega\beta+\gamma}{3}}$$

が成り立ちます
ここで $${A=\alpha+\omega\beta+\omega^2 \gamma,\ B=\alpha+\omega^2 \beta+\omega\gamma}$$ を
3次のラグランジュ・リゾルベントといいます
これを使うと先ほどの式は

　$${\displaystyle \alpha=\frac{\alpha+\beta+\gamma}{3}+\frac{A}{3}+\frac{B}{3}}$$

　$${\displaystyle \beta=\frac{\alpha+\beta+\gamma}{3}+\frac{\omega^2 A}{3}+\frac{\omega B}{3}}$$

　$${\displaystyle \gamma=\frac{\alpha+\beta+\gamma}{3}+\frac{\omega A}{3}+\frac{\omega^2 B}{3}}$$

よって、$${A}$$ と $${B}$$ について全ての入れ替えで不変であったり、$${A}$$ と$${B}$$ の式に関して不変であるようになればいいわけです

そこで、3つの解の入れ替えを考えると

の6通りがあり、②〜⑥の入れ替えでは不変になりません
（対称式でない）
しかし、$${A^3,\ B^3}$$ で入れ替えを行うと（頑張って計算すると）
　$${A^3 \gets①\to A^3}$$
　$${A^3 \gets②\to B^3}$$
　$${A^3 \gets③\to B^3}$$
　$${A^3 \gets④\to B^3}$$
　$${A^3 \gets⑤\to A^3}$$
　$${A^3 \gets⑥\to A^3}$$
と2つに落ち着きます
$${A^3-B^3}$$ のついて②〜④の入れ替えを行うと、$${B^3-A^3}$$ と符号だけ異なるので、2次方程式のときのように$${(A^3-B^3)^2}$$ を考えると、②〜④のときも対称性が成り立ちます
よって、3次の基本対称式 $${\alpha+\beta+\gamma,\ \alpha\beta+\beta\gamma+\gamma\alpha,\ \alpha\beta\gamma}$$ で表すことができます
$${A^3+B^3}$$ も①〜⑥に関して対称性が成り立つので、基本対称式で表すことができます
よって、$${A^3,\ B^3}$$ も基本対称式で表すことができます
基本対称式は3次方程式の係数 $${a,\ b,\ c,\ d}$$ で表すことができるので、$${A^3,\ B^3}$$ も係数 $${a,\ b,\ c,\ d}$$ で表すことができます

つまり

$${\begin{array}{ccccc} 係数で表される式 & 　 & 　 &　& 解で表される式 \\ (A^3-B^3)^2 & \longleftrightarrow & A^3,\ B^3,\ A^3-B^3 & \longleftrightarrow & A,\ B \\ ①〜⑥で恒等式 &　& ①⑤⑥で恒等式　& 　 & ①のみで恒等式 \end{array}}$$

が言えます
振り返って2次方程式をみてみると

$${\begin{array}{ccc} 係数で表される式 & 　 &  解で表される式 \\ (\alpha-\beta)^2 & \longleftrightarrow & \alpha-\beta \\ \mathrm{(a),\ (b)} の両方で恒等式 &　& \mathrm{(a)} のみで恒等式 \end{array}}$$

と同じようなことが言えます

群とは

ここで置き換え①〜⑥についての性質について考えてみましょう

群の定義
　1。演算$${*}$$について閉じている
　　（演算結果が元になっている）
　2。任意の元（要素）に対して、結合法則が成り立つ
　　（$${a*(b*c)=(a*b)*c}$$が成り立つ）
　3。単位元$${e}$$が存在する
　　（恒等変換になるもの。$${a*e=e*a=a}$$）
　4。任意の元$${a}$$に対して、その元に対する逆元 $${ a^{-1}}$$ が存在する
　　（演算すると単位元になるもの。$${a*a^{-1}=a^{-1}*a=e}$$）

この考えによると3次方程式の置き換えで出てきた①〜⑥は群になっています

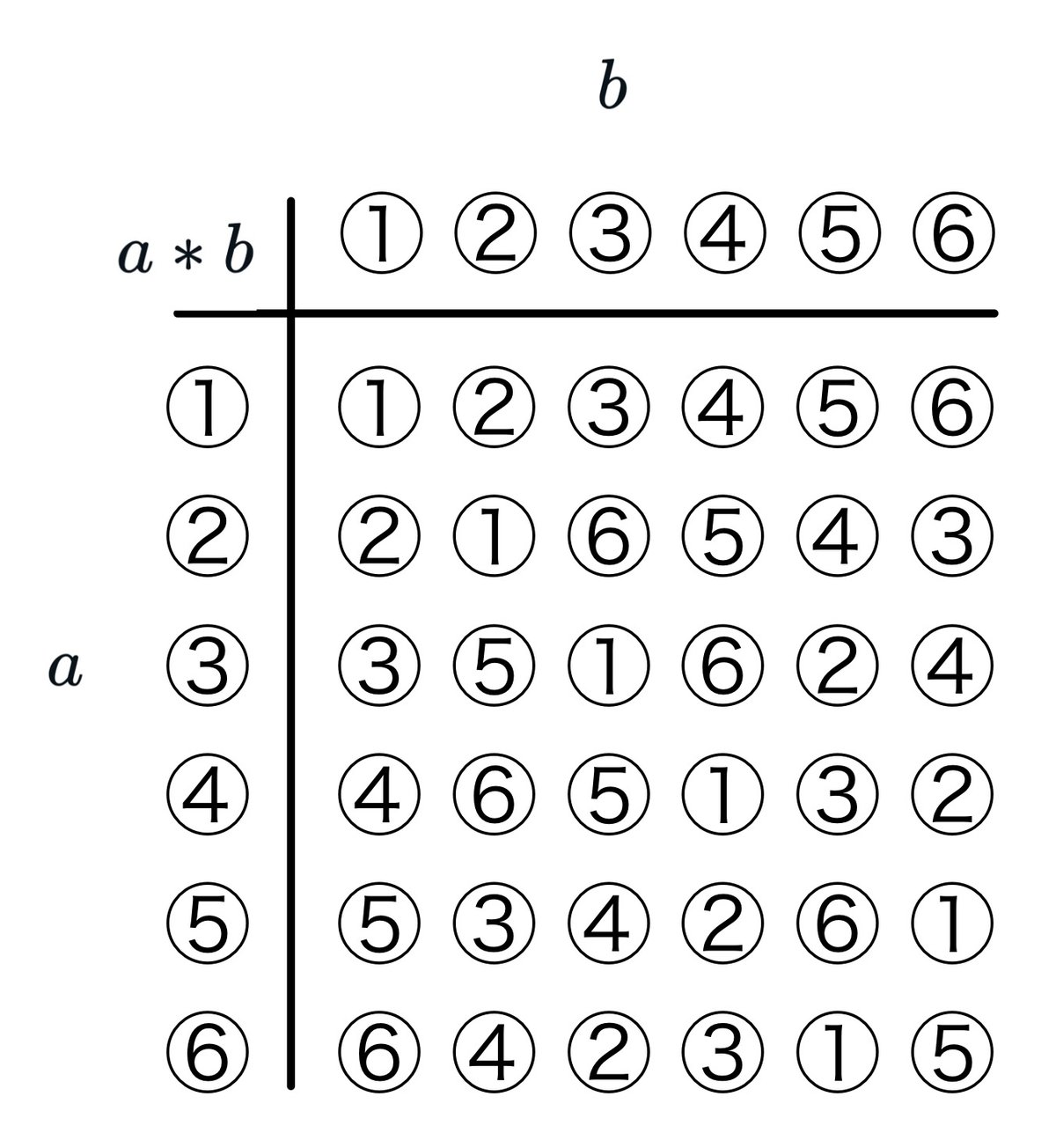
正規部分群
　1。部分群とはある群の一部分でできた群のこと
　　　例えば、群 $${G=\{e,\ a,\ a^2,\ b,\ ba,\ ba^2\}}$$ に対して $${H=\{e,\ a,\ a^2\}}$$をいう
　　　 $${G=\{①,\ ②,\ ③,\ ④,\ ⑤,\ ⑥\}}$$ に対していえば、
　　　$${\{①,\ ②\},\ \{①,\ ③\},\ \{①,\ ④\},\ \{①,\ ⑤,\ ⑥\}}$$ が
　　　それぞれ部分群になります

　2。部分群による割り算とは余りなくグループ化できるもの
　　　例えば、$${G/H=\{e\{e,\ a,\ a^2\},\ b\{e,\ a,\ a^2\}\}=\{eH,\ bH\}}$$
　　　$${G=\{①,\ ②,\ ③,\ ④,\ ⑤,\ ⑥\},\ H=\{①,\ ⑤,\ ⑥\}}$$ のとき
　　　$${G/H=\{①\{①,\ ⑤,\ ⑥\},\ ②\{①,\ ⑤,\ ⑥\}\}=\{①H,\ ②H\}}$$ と
　　　なるので割り算ができます

　3。正規部分群とは割った結果が群であるとき割った群をいう
　　　例えば、$${\{eH,\ bH\}}$$ が群であれば、$${H}$$ は $${G}$$ の正規部分群という

巡回群
　単一の元によってつくられる群
　$${\{e,\ a\}=\{a,\ a^2\}}$$ や $${\{e,\ b,\ b^2\}=\{b,\ b^2, b^3\}}$$ は巡回群になる

例えば $${H=\{①,\ ⑤,\ ⑥\}}$$ は
　$${⑤*⑤=⑥,}$$
　$${⑤*⑥=①}$$
なので、巡回群です

方程式に解の公式がある条件

方程式に解の公式がある条件は
　正規部分群で割ってできた群が全て巡回群である
ということである

これを見つけたのは、フランスの19世紀の数学者エヴァリスト・ガロアです
3次方程式でいえば

　　$${\begin{array}{ccccc} 係数で表される式 & 　 & 　 &　& 解で表される式 \\ (A^3-B^3)^2 & \longleftrightarrow & A^3,\ B^3 & \longleftrightarrow & A,\ B \\ ①〜⑥で恒等式 &　& ①⑤⑥で恒等式　& 　 & ①のみで恒等式 \\ \\ G=\{①,\ ②,\ ③, &　& H=\{①,\ ⑤,\ ⑥\} &　& E=\{①\} \\ 　　　　④,\ ⑤,\ ⑥\} &　&　&　&　 \\ 　&　& G/H は巡回群 & 　& H/E は巡回群 \\ \end{array}}$$

となるので解の公式があるのです

5次方程式に解の公式がないとは
　5個の解の置き換え120個を群 $${G}$$ と考えると、60個の元でできた群 $${H}$$ で割ることが可能で、できた群 $${G/H}$$ は巡回群になっています（←ここはOK）
しかし、この群 $${H}$$ はどのように部分群を作って割り算しても、できあがった群は巡回群にはならないのです（←ここがダメ）

ガロアの人生

これを思いつき論文にしたのはガロアが18歳のときです
しかし受け取ったフーリエが死去したため紛失してしまいます
また、新聞への投書をきっかけに共和主義活動をしていたとみなされ、通っていた学校を追放されてしまいます

翌年もう一度提出した論文はポアソン達によって却下されます
さらに共和主義活動をしたとして逮捕され、刑務所に入れられてしまいます

論文の審査が順調ならば政治活動に走らなかったかもしれません

この頃流行していたコレラに伴い、入っていた刑務所から療養所へ移されます
そしてここで医者の娘と運命的な出会いがあります
彼女を巡ってか政治活動によるものなのか分かりませんが、決闘し20歳の若さで亡くなります

決闘の前日、親友に宛てた手紙と徹夜で推敲した論文がガロアの残したものでした
「僕にはもう時間がない」という一言を手紙に記して……

決闘で傷付いたガロアの元に彼の弟が駆けつけます
涙ぐむ弟に、ガロアは次のように言ったといいます
「泣かないでくれ。二十歳で死ぬのには、ありったけの勇気が要るのだから！」
これがガロアの最後の言葉となり、翌日には息を引き取ります

短すぎる一生
長生きしていればどんな素晴らしい数学の研究がなされていたか分かりません