
企業価値評価:Feltham-Ohlson[1995]モデル
前回は、Ohlson[1995]モデルに付随する「その他の情報」の観測不能問題を解消し、実務的な完成度を高めたOhlson[2001]モデルについて議論した。今回は、Ohlson[1995]モデルの別の発展モデルであるFeltham-Ohlson[1995]モデルを取り上げる。このモデルは企業活動を営業活動と財務活動に分類する点が特徴的だが、そのような問題提起の背景に触れ、Feltham-Ohlson[1995]モデルを導出し、背後の仮定に関する理解を深める。前回はこちら。
なぜ企業活動を営業/財務活動に分けるのか?
Feltham-Ohlson[1995]モデルはOhlson[1995]モデルの発展形であり、企業活動を営業活動と財務活動に分類した概念で捉えるという特徴を有している。
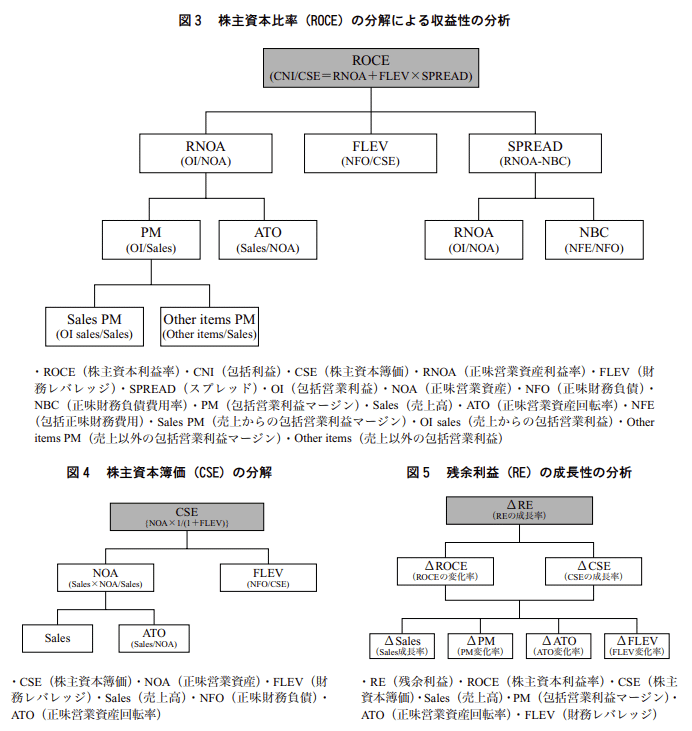
現行の会計制度に基づく財務諸表においては、営業活動に関する資産・負債と財務活動に関する資産・負債の明確な分類が困難だが、その有用性については指摘されてきた。この発想は米国における財務分析の第一人者として知られるPenmanの提唱する「企業評価と理論的に直接結びついた財務比率分析」の特徴の一つであり、従来のアドホック的な(=明確な理論的フレームワークを有していない)財務比率分析に代わる新たな手法として注目されている。その骨子は、残余利益モデル(RIM)に基づき企業の営業活動と財務活動を明確に区分したうえで、ROE、株主資本簿価、ターミナルバリューを以下の図のように分解するアイデアである。
また、IASB(国際会計基準審議会)とFASB(米国財務会計基準審議会)が2008年10月に公表したディスカッションペーパー「財務諸表の表示に関する予備的見解」の中では、財務諸表を事業セクションと財務セクションに分類して表示する案が提示されており、IFRS(国際財務報告基準)は将来的に、資産や負債に関して営業活動や財務活動別の分類表記を求める可能性がある。
例えばトヨタ(7203)は現在IFRSを採用しているが、以下の通り連結財政状態計算書を主力の自動車製造・販売を手掛ける「自動車等セグメント」と主に販売金融事業を手掛ける「金融セグメント」に区分して開示している。
このようにセグメント別にP/L、B/Sを区分することで、本業の収益力をより正確に評価することが可能になり、更に例えば完成車メーカーの中で販売金融機能を有するトヨタ・日産・ホンダと、販売金融機能を持たないマツダ・スズキ・SUBARUなどとの比較分析も容易に行えるなどの利点がある。

このように、企業価値評価において企業の営業活動と財務活動とを区別して捉えるFeltham-Ohlson[1995]モデルへの注目が今後高まる可能性があり、理論・実務の両面で押さえておくべき重要なモデルだと言えよう。
Feltham-Ohlson[1995]モデル
Feltham-Ohlson[1995]モデルでは、以下の財務利益関係、クリーン・サープラス関係(CSR)、そしてFeltham-Ohlson[1995]線形情報ダイナミクス(LID)の3つが成立すると仮定している。
財務利益関係:$${i_t=r\cdot fa_{t-1}}$$
クリーン・サープラス関係(CSR):
$${fa_t=fa_{t-1}+i_t-d_t+c_t}$$
$${oa_t=oa_{t-1}+ox_t-c_t}$$
Feltham-Ohlson[1995]線形情報ダイナミクス(LID):
$${\tilde{ox}_{t+1}^a=\omega_{11}ox_t^a+\omega_{12}ao_t+\nu_{1, t}+\tilde{\varepsilon}_{1, t+1}}$$
$${\tilde{oa}_{t+1}^a=\omega_{22}oa_t+\nu_{2, t}+\tilde{\varepsilon}_{2, t+1}}$$
$${\tilde{\nu}_{1, t+1}=\gamma_1\nu_{1, t}+\tilde{\varepsilon}_{3, t+1}}$$
$${\tilde{\nu}_{2, t+1}=\gamma_2\nu_{2, t}+\tilde{\varepsilon}_{4, t+1}}$$
但し、$${c_t}$$はフリー・キャッシュフロー、$${\omega_{11}\in [0, 1)}$$は残余営業利益の持続性を表すパラメータ、$${\omega_{12}≥0}$$は保守主義を表すパラメータ、$${\omega_{22}\in [1, 1+r)}$$は純営業資産の成長性を表すパラメータ、$${\gamma_1}$$と$${\gamma_2}$$は「その他の情報」の持続性を表すパラメータ($${|\gamma|<1}$$)、$${\varepsilon}$$は期待値ゼロの誤差項である。
Feltham-Ohlson[1995]モデルの第1の特徴は、資本を純営業資産と純財務資産に分解し($${b_t=oa_t+fa_t}$$)、利益を営業資産から生じる営業利益と、財務資産から生じる財務利益に分解している点である($${x_t=ox_i+i_t}$$)。
第2の特徴は、財務利益関係($${i_t=r\cdot fa_{t-1}}$$)を仮定している点である。このことは、財務資産及び財務負債はともに時価評価されており、また財務資産及び財務負債に対する利子率は等しいことを意味している。この時、
$${x_t^a=x_t-r\cdot b_{t-1}=(ox_t+i_t)-r(oa_{t-1}+fa_{t-1})=ox_t-r\cdot oa_{t-1}=ox_t^a}$$
となり、残余利益と残余営業利益は一致する。つまり、財務利益関係の仮定の下では企業の残余利益は純営業資産からのみ発生することになる。
第3の特徴は、Feltham-Ohlson[1995]線形情報ダイナミクス(LID)において、残余営業利益の発生源として、超過収益力の持続性以外に、純営業資産を追加している点である。この純営業資産の係数$${\omega_{12}}$$は、$${0≤\omega_{12}}$$と想定されているが、等号成立は純営業資産が時価評価されているときであり、現行の保守主義会計の元では$${0<\omega_{12}}$$となることが想定されている。つまり、保守主義会計によって純営業資産が時価よりも低い価額で計上されていることが、残余営業利益の発生源泉となっていると考えている。
Feltham-Ohlson[1995]は、配当割引モデル(DDM)に財務利益関係、CSR、LIDの関係式を代入し、以下の評価モデルが得られることを示した。
Feltham-Ohlson[1995]モデル
$${P_t=b_t+\dfrac{\omega_{11}}{1+r-\omega_{11}}ox_t^a}$$
$${+\dfrac{\omega_{12}(1+r)}{(1+r-\omega_{11})(1+r-\omega_{22})}oa_t}$$
$${+\dfrac{1+r}{(1+r-\omega_{11})(1+r-\gamma_1)}\nu_{1, t}}$$
$${+\dfrac{\omega_{12}(1+r)}{(1+r-\omega_{11})(1+r-\omega_{22})(1+r-\gamma_2)}\nu_{2, t}}$$
しかしながら、Ohlson[1995]モデル同様、この評価モデルでは「その他の情報($${\nu_{t, 1}, \nu_{t, 2}}$$)」が観察不可能である。そこで、両辺に$${t}$$期における期待値をとり、他の情報を観察可能な以下の形で表す。
$${\nu_{1, t}=E_t[\tilde{ox}_{t+1}^a]-\omega_{11}ox_t^a-\omega_{12}oa_t}$$
$${\nu_{2, t}=E_t[\tilde{oa}_{t+1}]-\omega_{22}oa_t}$$
上式を評価モデルに代入すると、次の観察可能な評価モデルが得られる。
$${P_t=b_t+\dfrac{1}{(1+r-\omega_{11})(1+r-\gamma_{1})}(-\omega_{11}\gamma_{1}{ox}_t^a+(1+r)E_t[\tilde{ox}_{t+1}^a])}$$
$${-\dfrac{\omega_{12}(1+r)\{\omega_{22}\gamma_2-\omega_{22}\gamma_1+\gamma_1(1+r)-\gamma_1\gamma_2\}}{(1+r-\omega_{11})(1+r-\omega_{22})(1+r-\gamma_{1})(1+r-\gamma_{2})}{oa}_t}$$
$${+\dfrac{\omega_{12}(1+r)}{(1+r-\omega_{11})(1+r-\omega_{22})(1+r-\gamma_{2})}E_t[\tilde{oa}_{t+1}]}$$
いま、純営業資産の係数$${\omega_{12}}$$がゼロであると仮定すると、上式は
$${P_t=b_t+\dfrac{1}{(1+r-\omega_{11})(1+r-\gamma_{1})}(-\omega_{11}\gamma_{1}{ox}_t^a+(1+r)E_t[\tilde{ox}_{t+1}^a])}$$
となる。さらに、財務利益関係の仮定のもとでは$${x_t^a=oa_t^a}$$であるので、
$${P_t=b_t+\dfrac{1}{(1+r-\omega_{11})(1+r-\gamma_{1})}(-\omega_{11}\gamma_{1}x_t^a+(1+r)E_t[\tilde{x}_{t+1}^a])}$$
となり、Ohlson[2001]モデルと一致する。Feltham-Ohlson[1995]モデルにおいて$${\omega_{12}=0}$$という制約は、純営業資産も純財務資産と同様に時価評価されているということを意味している。また、財務利益関係の成立を仮定しているということは、財務資産及び財務負債に対する利子率が等しいということを意味しており、この場合には残余利益と残余営業利益は等しくなる。
これらのことから分かるように、Feltham-Ohlson[1995]モデルとOhlson[1995/2001]の相違点は、前者が1)会計における保守主義を考慮していること、2)財務利益関係の成立を仮定していることの2点である。
次回は、Ohlson[1995]モデルの別の発展形である、株主による経営者の動機付けに焦点を当てたOhlson[1999]モデルに対する理解を深めたい。
