投票のパラドックス

　投票によって何かを決める場合、多数決が唯一の方法ではありません。他にもいろんな決め方があります。
　評価者の第１順位の票数が最も多いものを選ぶ方法が「多数決」ですが、死票が多くなるきらいがあります。第１順位の票数の上位２者で再投票を行うやり方が「決選投票」で、この方式では最後に過半数の支持を得て当選します。
　いまＡ,Ｂ,Ｃの３案に対して、評価者９人の優先順位が次のようだとします。
　　　　人数│　４　　３　　２
　　　　──┼─────────
　　　　１位│　Ａ　　Ｂ　　Ｃ
　　　　２位│　Ｃ　　Ｃ　　Ｂ
　　　　３位│　Ｂ　　Ａ　　Ａ

(1)　多数決では［　　］案が選ばれます。決選投票では［　　］案が選ばれます。
(2)　他の選び方を提案してください。また、その方法で選ばれるものを明記してください。
（多数決でも決選投票でも選ばれないものが選ばれるような方法をぜひ！）

◇　　　　　　　◇　　　　　　　◇

(1)　「多数決」では第１順位の最も多いＡが選ばれます。
　「決選投票」では、初めに第１順位の上位２者としてＡとＢが選ばれて、ＡとＢで決選投票を行うと「第１順位にＣを選んだ２人がＢ支持に回ります」から、Ａ４票に対してＢは５票を得て、最終的にＢが選ばれます。

(2)
例１：「１位に３点、２位に２点、３位に１点」を与えてその合計点の最も多いものを選ぶ方法（「順位評点法」または「ボルダ・ルール」）。
　その方法では、Ａ：３点×４人＋１点×５人＝17点、Ｂ：３点×３人＋２点×２人＋１点×４人＝17点、Ｃ：３点×２人＋２点×７人＝20点となって、最多得点のＣが選ばれる。

例２：１人が２票を投票する。（ただし、同じ人に２票投票することはできない。）
　この場合、「Ａが４票、Ｂが５票、Ｃが９票」獲得して、Ｃが選ばれる。

例３：相応しくない候補者（最も優先順位が低い候補者）を投票して、投票数の最も少ない人を選ぶ。
　この場合、「Ａが５票、Ｂが４票、Ｃが０票」獲得して、Ｃが選ばれる。

など。

　結局のところ、投票による決め方に「全員が納得するような絶対的な公平さ」というものは無いんですね。これを「アローの不可能性定理」と言います。

　ところで、この例よりもっと強烈なバージョンが慶應大学・総合政策学部2018年度入試の「小論文」に出ています。

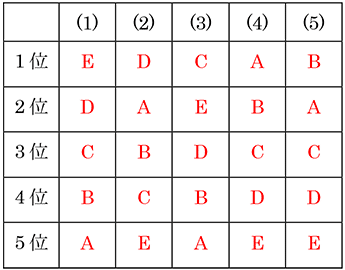
　ある政党に所属する国会議員は51名おり、彼（彼女）らの中から党首を選ぼうとしている。今、A 氏、B 氏、C 氏、D 氏、E 氏の５人が立候補したとする。ここで、51名の議員（立候補者自身を含む）は各候補者に対して、右表（↑上表）にあるような党首としての望ましさの順位を付けているものとする。
　次に、党首選のルールについて考える。

(1)　単純多数決
　全員が１位の候補者に投票し、得られた票数が１番多い候補者が選ばれるルールを単純多数決と呼ぶ。

(2)　決選投票付き多数決
　上記の単純多数決で選ばれる E の得票数は 17 票だが、議員は 51 名いるので 26 票以上で過半数であることから、E の票数は過半数に満たない。この時、票数の１位と２位で決選投票を行い、票数の多かった（過半数を得た）方の候補者が選ばれるルールを決選投票付き多数決と呼ぶ。

(3)　逐次消去法
　全員が１位の候補者に投票し、得られた票数の１番少ない候補者を除いた上で、再度全員が投票を行う。但しこの時、投票した候補者が除かれた議員は、除かれていない者の中で最上位の候補者に投票することになる。こうして最低得票数の候補者を１人ずつ除きながら投票を繰り返していき、最後に残った候補者が選ばれるルールを、逐次消去法と呼ぶ。

(4)　ペアごとの多数決
　候補者のペア（全部で10通り）ごとに投票を行い、いかなる相手に対しても票数で上回る候補者（ペア全勝者と呼ばれる）が選ばれるルールを、ペアごとの多数決と呼ぶ。例えば、A と B のペアに対する投票の場合は、A が 26 票、B が 25 票となるので、A が B に票数で上回る（A が B に勝利する）ことになる。

(5)　順位評点法
　議員ごとに１位の候補者に４点、２位の候補者に３点、３位の候補者に２点、４位の候補者に１点、５位の候補者に０点を付けて、候補者ごとに点数を合計し、最多得点を獲得した候補者が選ばれるルールを、順位評点法と呼ぶ。

問１　上記の５つのルールでは、１位の候補者が党首として選ばれるだけではなく、ごく自然に５人の候補者の１位から５位までの順位を決まることができる。ルールごとの５人の候補者の順位を答えよ。
※　決選投票付き多数決で第２位以下を決めるときには、すでにランクの決定した候補者を除外した上で決選投票付き多数決方式を採用する。

問２　・・・（中略）・・・簡潔に図示せよ。
問３　・・・（中略）・・・600字以内で答えよ。
問４　・・・（中略）・・・300字以内で紹介せよ。

　よかったら (1) だけでもやってみてください。

◇　　　　　　◇　　　　　　◇

◇　　　　　　◇　　　　　　◇

〜 数学目線で社会を見る 〜
▷ 投票のパラドックス　　　　
▷ 信用創造という名の錬金術　
▷ シェア・タクシーの割り勘定