立方体と正四面体の展開図

2021年6月20日 06:00

立方体の展開図（全11種）

　立方体の展開図を全パターン描いてみた。平行移動・回転・裏返しして同じになるものは同じものとみなすと、たぶん次の11種類だと思う。間違っていたら、教えてください。

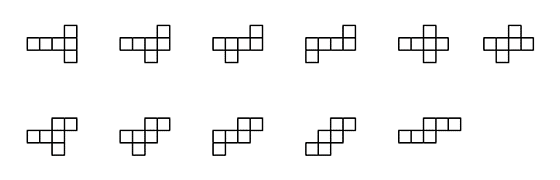
　というか、「上のうち間違っているものを選び、他とカブらないように正しく直せ」なんて問題をどこぞの試験に出したら、出来ないだろうなぁ。いや、僕も出来そうにないが。

　次は正四面体でやってみよう。面が少ない分、簡単か。もしくは角度が直角じゃない分、難しいか。どちらにせよ、立方体であれ正四面体であれ、やってみなきゃわからない。実際に紙に描いて、ハサミで切って、折ってみるのが一番なんだろうな。
　いろんなことをスマホでやるようになって、立体物でも何でもかんでも画面という平面上で認識するようになった。その際にユーザーが立体感を感じられるように、裏方でクリエイター達が工夫すればするほど、僕らの立体認識能力は落ちていくんだろうな。たぶんすでにだいぶ落ちているんだと思う。
　それに対抗するには、リアルに立体物を扱うことが大事。そう、紙に描いて、ハサミで切って、折ってみる、そういう経験を学校の授業でやった方が良いんじゃないか。やってみると、楽しいんじゃないかな。

正四面体の展開図全パターン

　正三角形４つを最低１つの辺が重なるように置く置き方は、次の３つしかない。つまり、正四面体の展開図の候補はこの３つだけです。

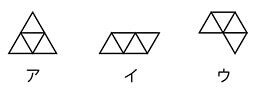
　では、ここで【問題】です。上のア,イ,ウを正四面体の展開図になるものとならないものに分けてください。

◇　　　　　　◇　　　　　　◇

《答》正四面体の展開図になるものはアとイで、
　　　正四面体の展開図にならないものはウです。
　立方体の展開図は全部で11種類ありましたが、正四面体の展開図は２種類だけなんですね。

11種類をランダムに配るとき、全種類そろうにはいくつ配ればよいか？

　上の記事「立方体の展開図（全11種）」をFacebookに投稿したところ、ある人が「小学生の時の塾の先生が立方体の展開図のシールを配って、11種類全部そろえた」という思い出をコメントしてくれました。私は「それを渡されれば自然と頭の中で組み立てるだろう。なるほど、良いやり方だ」と思いました。
　そして気になったのが「１枚ずつランダムに配るとして、何枚くらい配れば全種類そろうのか？」ということ。その確率計算は結構難しい。２日間ずっと考えて、ようやく結論が出ました。

　次のグラフは、横軸が「配る枚数」で、縦軸が「全11種類そろう確率」です。
　枚数が10枚以下なら確率は当然ゼロ。11枚配ってその時点で11枚が全部異なる確率は0.01％ほどで、つまり現実にはほとんど起こりません。20枚配ると10％を超えて、クラスの中に全種類そろう人がパラパラ出始めます。30枚配ると50％を超えて、つまりクラスの約半数が全種類そろいます。
　そこから先は全種類そろう確率が意外と伸びずに、その確率が90％に達するのは50枚配った時、99％を超えるのは74枚配った時です。友達同士で交換すれば、もっと早くそろうでしょうけれど。

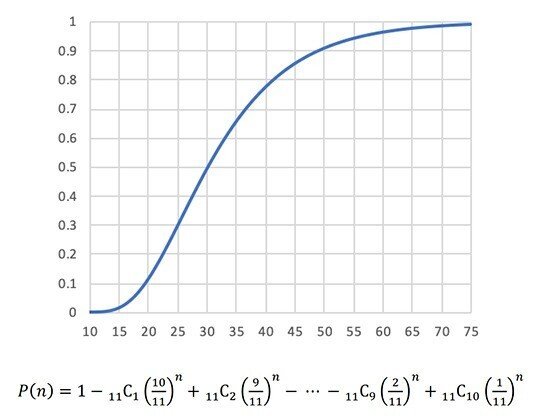
　計算式は上の通りで、だいぶややこしい。手計算できるはずもなく、もちろんエクセルを使いました。式中の「11」を「６」に変えれば、「サイコロを何回振れば１〜６の目が全部出るか」に対応します。