エクセルの限界に挑む

　コンピュータは突き詰めれば電気のオン・オフ（電気が流れているか、いないか）で制御しています（ただし量子コンピュータについてはその限りでない）。つまり２進法。もちろん、エクセルもです。そして、それゆえの限界もあります。コンピュータの宿命です。
　私たちはたまたま10進法に慣れ親しんでいますが、コンピュータとうまく付き合うには２進法にも慣れ親しんでおきましょう。その感覚は、論理式でも指数・対数でも役立ちます。
　では、ここでエクセルの計算の仕方を確認しながら、その限界に挑んでみましょう。

エクセルはどこまで正確に計算できるか？

　手元にある電卓で「1÷3×3＝」と入力すると、「0.9999999」という結果になった。「1÷3」は割り切れないので、電卓の中では計算結果が「0.3333333」となって、それを3倍して「0.9999999」になったというわけだ。
　ところで、同じ電卓で「1×3÷3＝」と入力したら、結果は「1」になった。電卓は入力した順番に計算すると考えれば、そうなることはなるほど納得できる。

　さて、エクセルはどこまで正確に計算できるのだろう？

(1)　セルA1に「=1/3」を入力して、小数点以下の表示ケタ数を増やしてみた。小数第何位まで正しく表示するだろうか？　（※1 をクリック）

(2)　セルB1に「=1/2」を入力して、セルB2に「=B1/2」を入力して、セルB2の式を下方向にコピーした。何行目まで正しく表示するだろうか？

(3)　セルC1に「=2」を入力して、セルC2に「=C1＊2」を入力して、セルC2の式を下方向にコピーした。何行目まで正しく表示するだろうか？
　（ただし、(3)のC列では ※2 の▼印をクリックして、「数値」を選ぶ）

その結果・・・

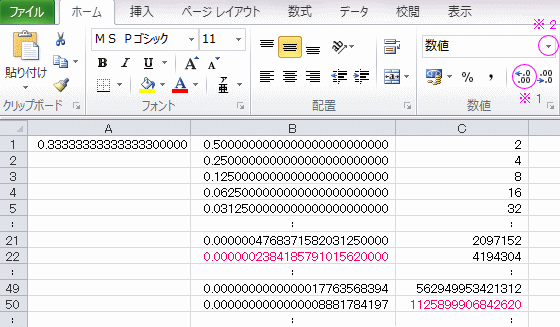
(1)　小数点以下20位まで表示してみたところ、「3」が15個並んで、それ以降は0となった。これは小数第16位を四捨五入して、小数点以下15位までで表した値と一致する。

(2)　21行目までは正しく表示したが、22行目で値が合わなくなった。
　　21行目（1/2の21乗の値）は 0 でない数が小数第7位から小数第21位まで続く数であるが、つまり15ケタ分は正しく表示したことになる。
　　22行目（1/2の22乗の値）は 0 でない数が16個続く数になるが、15個までは正しく表示して、16個目の数字が 0 になってしまっている。

(3)　49行目までは正しく表示したが、50行目で値が合わなくなった。
　　49行目（249 の値）は15ケタの整数で正しく計算したが、
　　50行目（250 の値）は16ケタ目が 0 になってしまっている。

　以上 (1),(2),(3) からわかること。それは、エクセルは有効数字にして15ケタ程度までは正しく計算できるが、それ以上になると正しく計算できなくなるということだ。
　15ケタというと、整数値の場合、数百兆のレベルになる。それを超えた数、つまり一千兆のレベルはエクセルで正確には計算できないことになる。では、エクセルでは一千兆を超えた数は扱えないのかというと、そういうことではない。

エクセルはどこまで大きな数、細かい数を扱えるか？

(1)　セルA1の値を 10 として、セルA2の式を「= A1＊10」として、
　　その式を下方向にコピーする。
(2)　セルB1の値を 0.1 として、セルB2の式を「= B1/10」として、
　　その式を下方向にコピーする。
（ただし、セルの表示形式は「標準」のままとする）

　ところでこの場合、値が大きくなると、あるいは 0 に近い値になると、指数形式で表示される。たとえば、セルA11の「1E+11」は「1×10^11」を表し、セルB10の「1E-10」は「1×10^(−10)」を表す。
　さて、下方向にコピーしたとき、どこまで大きな数、細かい数を表せるか？

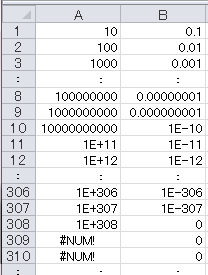
　A 列では 1×10^308 までは表示できたが、それより大きくなると「エラー」表示が出た。B 列では 1×10^(−307) までは表示できたが、それより細かい値になると「0」と表示された。
　ところで、これは「整数値は 308 ケタまで、小数は小数点以下 307 位まで『正確に』計算できる」ということではない。エクセル内部では値を
　　　　　　　a ×10^b　（ただし、1 ≦ a＜10 , b は整数）
の形で表現しているが、仮数部 a と指数部 b の精度が異なるからである。いうなれば、値の正確さは a で、値の大きさは b で決まる。上の例は、正確さを調べたのではなくて、扱える数の大きさを調べたのである。前の記事 で示したように、仮数部 a が正確に計算できるのは 15 ケタ程度である。すなわちエクセルでは、必ずしも正確とは限らないが、「およそ 10^(−307) から 10^308 程度までの計算を扱える」ということである。

浮動小数点形式はエクセルでこそ力を発揮する

　浮動小数点形式の数は「a×10^b」と表す。たとえば、10進数の 123 を浮動小数点形式で表すと 1.23×10^2 となる。また、２進数も浮動小数点形式で表すことができる。10進数の 123 を２進数で表すと 1111011 となるが、これを２進数の浮動小数点形式にすると 1.111011×10^110 となる。なお、この場合は、指数の部分も２進数表示したものだから、「×10^110」はつまり「×2^6」のことである。
　a を仮数部といい、b を指数部という。要するに、仮数部 a が数字の並びを表し、指数部 b が位取りを表すということだ。a が数の精度を表し、b が大きさを表すといってもよい。
　さて、コンピュータ内部では２進数で処理しているが、エクセルでは数を仮数部と指数部に分けて認識している。具体的には、仮数部に（符号も含めて）52ビット、指数部に（符号も含めて）12ビットを割り当て、合わせて64ビット（＝8バイト）を使って１つの数を表現している（「倍精度」の場合）。

※ 仮数部の先頭（整数部分）は必ず 1 なので、無視する。

　仮数部に52ビット割り当てた結果として10進数で15ケタまで正確に計算できる（→詳細は上の「エクセルはどこまで正確に計算できるか？」）ことになる。また、指数部に12ビット割り当てた結果として10進数で 10^300 のような大きな数や 10^(−300) のような細かい数も扱える（→詳細は上の「エクセルはどこまで大きな数、細かい数を扱えるか？」）ことになるというわけだ。

エクセルに計算ミスさせろ

　電卓に計算ミスさせるのは簡単です。「1÷3×3」を計算すると「1」にはなりません。「1÷3」は割り切れませんから、そこまで入力した時点で「0.333…」となって、続いて「×3」と入力すると「0.999…」と表示されます。
　一方、エクセルのセルに関数式「=1/3*3」を入力すると「1」と表示されます。エクセルはその程度では計算ミスしません。エクセルに計算ミスさせるには、もうちょっと工夫が必要です。

　比較的簡単な方法を１つ紹介しましょう。実はエクセルで「0.1を足し続ける」と60回目に計算ミスを起こします。
　具体的な手順を説明しましょう。まず各セルを小数点以下15ケタ以上表示するように設定してください。ホームリボンの「数値」の中の１つのボタンをクリックすることで設定できます。続いてセルA1に「0.1」と入力して、セルA2に関数式「=A1+0.1」を入力して、セルA2の式を下方向にコピーしてください。こうすると n 行目のセルの値は n/10 になるはずです。ところが60行目のセルA60の値は「6.000…」にはならずに、「5.999…」となってしまいます。61行目以降も所々で計算が合わないところが出てきます。
　他の数値でやってみましょう。0.5 と 1/3 でやってみたところ「0.5を足し続け」ても計算ミスは起こりませんでした（下の B 列）が、「1/3を足し続け」たら20行目で計算ミスしました（下の C 列）。
　ところで「0.1+0.1+0.1+…」と「0.1を足し続ける」と誤差が生じますが、「0.1×n」の計算をしても誤差が生じません。そのことを使うと、エクセルのシート上でどこで誤差が生じたのかをすぐに見分けるような関数式を作ることもできます。たとえば上記のようにA列に「0.1を足し続けた値」を表示させて、D列に「=IF(A列n行目の値=0.1×n,” ”,”誤差”)」のような式を入力すると、誤差が生じた行だけ「誤差」と表示されます。

エクセルはとことん２進法で計算する

　エクセルで実際にやってみたところ「0.5を足し続けても誤差を生じないが、1/3 や 0.1 を足し続けると誤差が生じ」ました。さて、その訳は、なぜなのでしょう？
　それは、10進数の 0.5 , 1/3 , 0.1 を２進数で表してみると分かります。エクセルでは10進数を入力して、計算結果を10進数で表示しますが、計算そのものは２進数で実行しているからです。
　まず、0.5 から。10進数の 0.5 を２進数で表すと 0.1 となります「0.5(10)＝1/2(10)＝1/10(2)＝0.1(2)」。つまり、２進数で表したとき、これは「割り切れる数（有限小数）」です。
　次に10進数の 1/3 を２進数にしてみましょう。そのために、まず分母の3を２進数にしてみると 11 となります。つまり、1/3(10)＝1/11(2) です。そこで、実際に割り算してみましょう。２進数の割り算は10進数の割り算と若干異なりますが、手順はほとんど同じです。
　同じように、10進数の 0.1 を２進数にしてみましょう。0.1(10)＝1/10(10) で、分母の 10 は２進数で 1010(２)ですから、２進数の割り算 1÷1010 を実行します。
　その結果は、次の通りです。

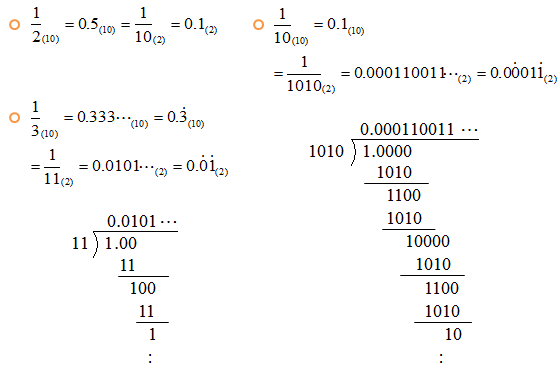
　10進数の 1/3 は割り切れない数（循環小数 0.3333…）ですが、２進数でも割り切れませんでした（循環小数 0.0101…）。10進数の 1/10 は割り切れる数（有限小数 0.1）ですが、２進数では 0.000110011… とこれも循環小数になりました。ですから、コンピュータの中では 1/3 や 0.1 を正確に計算することはできないのです。コンピュータは有限個のものしか扱えないので、無限小数はどこかの位で丸めて処理することになって、だから誤差が発生するのです。
　ちなみに、現行の学習指導要領では、上のような２進数の割り算や循環小数についても高校・数学で扱います。というわけで、この記事は高校・数学科と高校・情報科のコラボ・ネタです。

◇　　　　　　◇　　　　　　◇

　　　　　　　〜 デジタルの仕組み 〜
　　　▷ ２のｎ乗のザックリ計算
　　　▷ エクセルの限界に挑む
　　　▷ 天秤ばかりのおもりは、なぜ２進法なのか？