
情報伝達をグラフに=見える化する
うわさやデマが広まるのも、感染症が広がるのも、情報伝達の一種です。最初はゆっくりと、次第に急速に広がって、そしてやがて収まっていく。その様子をモデル化して、エクセルでシミュレーションしてみましょう。
情報伝達をグラフに=見える化する
まず、情報量(たとえば感染者数)の初期値(たとえば1人)を設定します。次に、情報の増加率(伝達率)を設定します。その上で、エクセルのセルに
○ 情報量=前の情報量 ×(1+増加率)
という関数式を入力してコピーして、情報量の推移をグラフにすると、指数関数のグラフが得られます。これは情報量が加速度的に(いわゆるねずみ算式に)無限に増えるグラフになりますが、感染症でもうわさでも人口を超えて増え続けることはありませんね。そこで、次に上限(人口)を設定することにします。
○ 情報量=前の情報量 ×(1+増加率)×(1ー前の情報量/上限)
こうすれば、情報量が上限に近づくにつれて増え方が穏やかになります。アルファベットのSのような形であることから「S字カーブ」と呼ぶことにしましょう。
けれどもこのモデルでは、最終的に上限(全人口)いっぱいまで広がって、一向に減らないことになりますから、もう一工夫しましょう。
ここでは一定時間(たとえば2週間)後に感染症が治ったり、うわさ話をしなくなったりして、その分だけ情報量が減少するようなモデルを考えます。そのために、まず「減少量」を設定してみました。
○ 減少数=一定時間前の増加数
けれども、これではまだ終息には至りませんでした。考えてみると、このモデルは「感染症が治った人が再び同じ感染症に罹っ」たり、「うわさ話に飽きてうわさをしなくなった人が、他の人から同じうわさ話を聞いて再びうわさ話をし始め」たりする状況ですから、実態にあいませんね。そこでさらに
○ 上限=情報が未達の人=全人口ーすでに情報を得た人
こうすることで、最初はゆっくりと、次第に急激に増えて、やがてピークに達して、そこから減少に転じて、最終的にはゼロに近づくような山型の波形になりました。「流行終息曲線」と呼ぶことにしましょう。
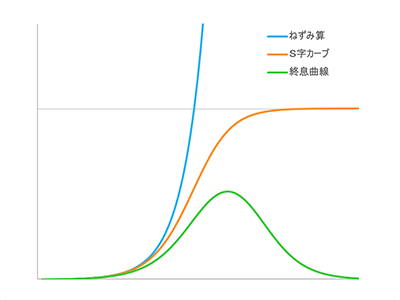
一般に、モノの増え方は直線的ではなくて、指数関数的(ねずみ算)です。でも、無限に増え続けるものでないことを考慮すると、モノの増え方はS字カーブになります。さらに、流行ったモノもやがて廃れるとすると、その波形は山型(流行終息曲線)になります。
エクセルシートならびに関数式は以下のようにやりました。
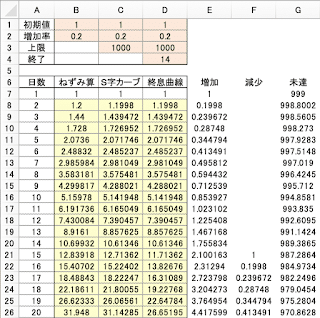
セルB8 : = B7*(1+B$2)
セルC8 : = C7*(1+C$2*(1ーC7/C$3))
セルD8 : = D7+E8ーF8
セルE8 : = D7*D$2*G7/D$3
セルF21 : = E7
セルG8 : = G7ーE8
倍々ゲームのリアリティー
1日で 10% 増えるなら、1.1⁷ =1.95 より7日で倍増する。
1日で 20% 増えるなら、1.2⁴ =2.07 より4日で 〃
1日で 30% 増えるなら、1.3³ =2.20 より3日で 〃
1日で 40% 増えるなら、1.4² =1.96 より2日で 〃
a 日で倍増するなら、2a 日で 4 倍に、
〃 3a 日で 8 倍に、
〃 4a 日で 16 倍になり、
〃 10a 日で 1,000 倍を超え、
〃 20a 日で 1,000,000 倍を超える。
机上の空論かと思いきや、世界で現実に起きている。
「3日で倍増、2週間で 30 倍、1ヶ月で 1,000 倍」・・・これくらいが普通みたい。
◇ ◇ ◇
〜 エクセルでシミュレーションする 〜
▷ 埃が風に舞う
▷ 情報伝達をグラフに=見える化する
▷ そのコイン、まとも? いかさま?
〜 新型コロナで確率・統計を学ぶ 〜
▷ コロナ渦中の確率計算
▷ サッカー観戦でコロナ感染者集計
▷ 情報伝達をグラフに=見える化する
