
人口ボーナス論(5)ー資本蓄積はいつまで続くのか?
はじめに
中国経済の重要な原動力は,人々の貯蓄とそれによる資本蓄積である。中国の経済成長を支えるこの資本蓄積がいつまで続くのかを明らかにしたい。
その際に,経済成長論で有名なソローモデルを利用して,資本蓄積の情況を考える。というのもソローモデルは定常状態という概念を提示しており,資本の限界生産性を考えると,いずれ経済は低成長に向かうので,その定常状態と中国の現実の経済との差を考えてみる。
ソローモデル
経済成長論でもっとも参照されるものにソローモデルがある。なお,記号の意味は「技術進歩は労働力人口を補っているのか」のものと同じである。
ソローモデルの資本蓄積方程式は以下のように示される(ソローモデルの詳細は参考文献のマクロ経済学の教科書などを参照のこと)。
$$
\Delta \tilde{k} = s\tilde{y} - (\delta + n + g) \tilde{k}
$$
ここで$${s}$$は貯蓄率,$${\delta}$$は資本減耗率,$${n = \frac{\Delta L}{L}}$$は労働力人口の成長率,$${g = \frac{\Delta E}{E}}$$は労働増大的な技術進歩率である。
ソローモデルの資本蓄積方程式の意味するところは,資本蓄積(効率労働1単位あたり)$${\Delta \tilde{k}}$$は,毎年の所得のうち貯蓄が投資に向けられること($${s\tilde{y}}$$)によって増加するが,固定資本の減価償却率$${\delta}$$,労働力人口の増加$${n}$$,労働増大的な技術進歩$${g}$$によって効率労働1単位の資本ストック$${\tilde{k}}$$が減るということである。労働増大的な技術進歩や労働人口の増加はそもそも1人あたりの労働活動が増えることであるので,その分1人当たりで見た場合には資本ストックが薄まる(希釈する)ことを意味している。
資本が増加する力と資本を薄める力が働いているソローモデルの資本蓄積方程式では,永遠に資本蓄積が続くわけではなく,最終的には以下の点で定常状態に到達する。
$$
s\tilde{y}=s\tilde{k}^{\alpha}= (\delta + n + g) \tilde{k}
$$
上記を解くと,定常状態の効率労働1単位あたりの資本蓄積レベルは以下のようになる。
$$
\tilde{k^*} = \left( \frac{s}{\delta + n + g} \right)^{1/1-α}
$$
ソローモデルの資本蓄積方程式を図で示すと以下のようになる。

効率労働1単位あたりの資本ストック水準が$${\tilde{k^*}}$$の左側にある限り,資本ストックは蓄積を続ける。$${\tilde{k^*}}$$の右側にある場合は,実際の資本ストックが薄まるので,資本ストックが減少する。この過程を通じて,経済の資本ストックの蓄積は定常状態において均衡する。これがソローモデルが示すものである。
ソローモデルの定常状態において,効率労働1単位あたりの資本ストックは一定となり,効率労働1単位あたりの生産も一定となる。ここで経済成長が止まるという意味ではなく,技術進歩率,労働力人口増加率,資本ストックの成長率が同じスピードになるという意味である。効率労働1単位あたりではなく,経済全体の成長率は
成長率=技術進歩率+労働力人口増加率
となる(詳細はマクロ経済学の教科書に譲る)。つまり定常状態では資本蓄積がこれ以上行われないので,技術進歩と労働力人口で決まることとなる。
また数式の展開は省くが,
1人あたりの生産(所得)の成長率=技術進歩率
となる。大胆なイメージで説明しておくと,定常状態では1人あたりの生産(労働生産性でもある)が一定となり,労働力と生産の関係が安定的になり,技術進歩のみが1人あたりの生産を決定するということである。
中国の実証分析
貯蓄率と定常状態
再掲すると,ソローモデルが想定する定常状態の効率労働1単位あたりの資本は以下の式で決定する。
$$
\tilde{k^*} = \left( \frac{s}{\delta + n + g} \right)^{1/1-α}
$$
この中の各種パラメーターはこれまでのデータ分析から
資本分配率$${\alpha=0.46}$$
減価償却率$${\sigma=0.14}$$
労働人口成長率$${n=-0.006}$$
技術進歩率$${g=0.055}$$
と設定する。問題は貯蓄率$${s}$$の設定である。ソローモデルでは貯蓄率の違いによって定常状態が移動する。つまり貯蓄率が増加すると図1の$${s\tilde{y}}$$が上に移動するので,その交点である$${\tilde{k^*}}$$は右に移動する。
中国の貯蓄率が30%強から50%へと前後していることから,この期間の定常状態の効率労働1単位あたりの資本ストックは上昇していると思われる。実際に,計算したものが図2である。
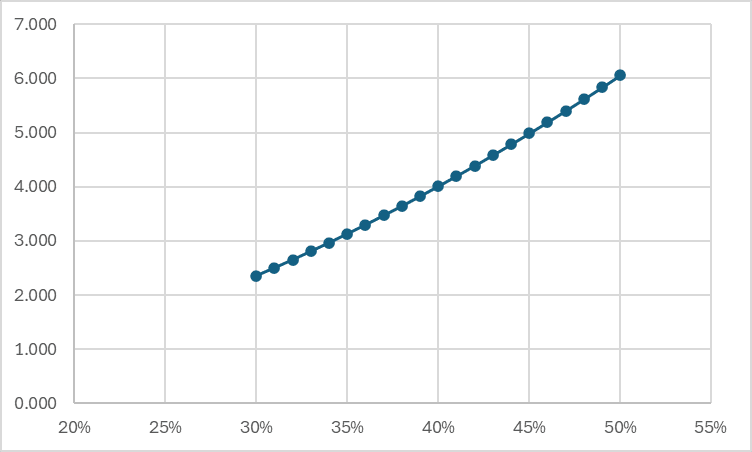
横軸は貯蓄率である。30%から1%ずつ上昇させて,定常状態の効率労働1単位あたりの資本ストック(縦軸)を計算した。これからもわかるように,貯蓄率が上昇すれば,それだけ定常状態の効率労働1単位当たりの資本ストックは上昇している。
中国は過剰蓄積か?
それでは貯蓄率$${s}$$をどう設定するか。ここでは,黄金律(Golden Rule)の貯蓄率を採用したい。そもそも貯蓄率が高くなると消費率は減少するので,人々の厚生は下がってしまう。理論的には,生産関数の限界生産性と人口成長率と技術進歩率が一致するところ,あるいは言い換えると,生産関数の資本分配率$${\alpha}$$と貯蓄率$${s}$$が一致するときの貯蓄率が定常状態かつ黄金律を達成する。すなわち貯蓄率$${s=0.46}$$である。
よって,黄金律(かつ定常状態)が達成されているときの理論的な効率労働1単位あたりの資本ストックの蓄積過程と実際の中国の効率労働1単位あたりの資本ストックの蓄積過程を比較することによって,中国の資本蓄積の情況が判断できる。その計算結果は以下のとおりである。

中国は2012年から資本蓄積が黄金律(かつ定常状態)を超えた資本ストックの蓄積が進んでいる。つまり,中国の消費が抑えられるほど貯蓄率は高く,それによって,過剰に資本蓄積が行われているという状況だ。
これを現実の中国経済に置き換えると,習近平政権以降,地方政府は融資プラットフォームを活用して,都市インフラを建設し,民間企業はそのインフラの下で不動産を積極的に開発してきていることの裏返しということだろう。
おわりに
過剰資本蓄積とは,丸川・梶谷(2015,pp.21-22)の言葉を借りると,「固定資本投資の収益性が低下し,明らかに投資を減らして消費を増やした方が経済厚生は増加するにもかかわらず,消費が抑制され,さらなる資本投資が持続的に行われるような状況」を指す。これは,「資産バブルの発生と非常に親和的」である(同p.22)。住宅が人々にとって投資の対象である中国では,2012年以降も投資が続き,理論が示唆する黄金律を超えた資本過剰経済になっている。
これまでの分析で,貯蓄率は高まっていること,投資率はさらに高くなっており,中国の過剰資本蓄積はかなりの程度進んでしまっていること,がわかった。
人口との関連でいえば,貯蓄を主体とする生産年齢人口が減少している中で,この過剰資本蓄積は続くのかどうか,さらなる検討が必要である。
というか,本稿の問題である「いつまでこの資本蓄積が進むのか」という解答はまだ得られていない。ただわかったことは,ここ10年すでにかなりの程度資本蓄積は進んでしまっているということだ。
参考文献
齊藤誠・岩本康志・太田聰一・柴田章久(2010)『マクロ経済学』有斐閣
二神孝一・堀敬一(2009)『マクロ経済学』有斐閣
丸川知雄・梶谷懐(2015)『超大国・中国のゆくえ4 経済大国化の軋みとインパクト』東京大学出版会
