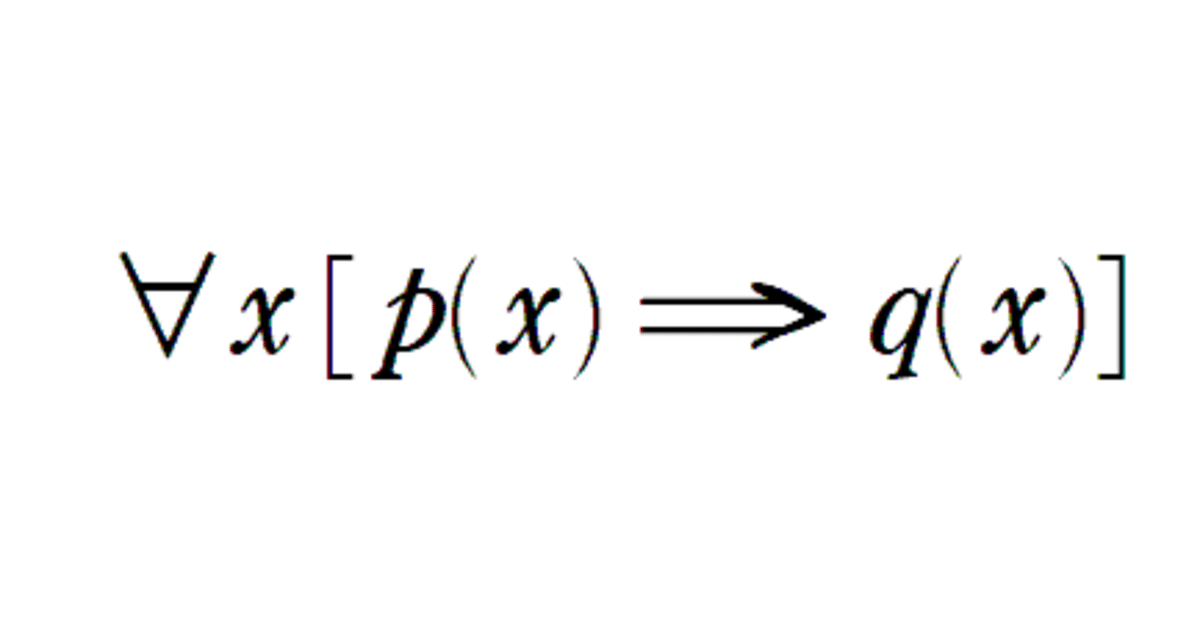
高校数学　教科書における p ⇒ q の記述の問題点・現場におけるアップデートのアイデア

　高校数学の教科書は、全称命題と存在命題についてあまり触れないように作られています。特に問題があるのは、p ⇒ q の記述です。そのため特に難関大を目指す生徒にとっては後々困ったことになりえます。また、大学入学後も ε-δ 論法などで苦労することになりかねません。
　もちろん、命題と条件の初学の段階では、数学の道具がほとんど整っていないので、あっさり扱って構わないと思います。ただし、難関大を目指すクラスでは、どこかの段階で命題と条件に関してのアップデートを計りたいところです。
　この note では、教科書における記述とその問題点について明らかにし、教科書と矛盾の少ない方向でアップデートする方法を模索します。

１．教科書の画像データ

　手元にある教科書と、その中の記述を貼ります（教科書の中身の検討をする際の画像利用は、許容されているはずです）。

２．p ⇒ q について

　p.55 に p ⇒ q についての記述があります。この記述は、大学以降の流儀とは大きく異なっています。
　本来は、次のような定義が普通だと思います。x は実数とします。
(1) まず命題 p, q に対して p ⇒ q の真偽を真理表により定義する。
(2) 次に、条件  0<x<4 ⇒ 2<x<6 は x=3, 5, 7 で真、x=1 で偽であることなどを確認する。
(3) ∀x [0<x<4 ⇒ 2<x<6 ] や ∀x [x>2 ⇒ x>1 ] は命題であることを確認し、それぞれの真偽を確認する。
　ところが、教科書の記述では p ⇒ q は常に全称化されてしまいます。これだと、数学的帰納法の説明で困ります。数学的帰納法は、n を自然数として
∀n [ p(n) ] ⇔ p(1) ∧ ∀n [ p(n) ⇒ p(n+1) ] を利用するんですが、教科書の記述では、p(1) ∧ {p(1) ⇒ p(2)} ⇔ p(1) ∧ p(2) を説明することができません。よって、苦肉の策として、数学的帰納法では ⇒ を使わずに日本語で説明しまくる方法で矛盾を回避しているように見えます。

３．反例について

　p.56 に反例が定義されていますが、これもあまりよくない表現です。本来ならば、全称命題 ∀x [p(x)] を否定するには、p(x) が偽となる x を一つ見つければよい、その理由は ￢(∀x [p(x)]) ⇔ ∃x [￢p(x)] というだけのことです。しかし、そこまでの中で全称命題と存在命題という概念が明示されていないので、突然存在命題が顔を出してしまう、というわけです。

４．アップデートの方法

　命題と条件の周辺をアップデートするには、ある程度学習が進んでから、再度ちゃんとやり直したほうがいいと思います。全称命題と存在命題は、じっくりと扱うとして、その時に問題になるのが教科書の p ⇒ q の記述との矛盾の解消です。教科書の記述を無かったことにする、ということも可能ですが、ここではそれをせず穏便にアップデートする方法を提案します。長岡亮介先生の「論理学で学ぶ数学」にヒントを得ました。

①例えば、実数 x について「x^2+1>0 が成り立つ」とは、∀x [x^2+1>0] が真であることをいう。つまり、「任意の x について p(x) が成り立つ」ことを単に「p(x) が成り立つ」という言い回しをする習慣がある。条件について真偽を考える場合は、 条件を全称化した命題について考える。
②よって、単に p(x) ⇒ q(x) と書いた場合は条件だが、これを命題として考えるときには ∀x [p(x) ⇒ q(x)] と考える習わしである。
③ただし、論理構造が複雑な場合は、∀x [p(x) ⇒ q(x)] と全称記号を明示することにしよう。

一応これで、矛盾を解消できると思います。

何かあれば加筆しますので、お気づきの点はお知らせください。