初学者向け・双曲線関数で遊ぼう

１．双曲線関数の定義

双曲線関数とは、次の式で定義されます。

$$
\cosh{x}=\frac{e^x+e^{-x}}{2},  \sinh{x}=\frac{e^x-e^{-x}}{2},  \tanh{x}=\frac{e^x-e^{-x}}{e^x+e^{-x}}
$$

なぜ双曲線関数と呼ぶかというと、双曲線の媒介変数表示に利用できるからです。これは、のちほど見ていきます。

２．双曲線関数の定義と、オイラーの公式の関連

$${\cosh{}}$$ という名前が、$${\cos{}}$$ との関連を匂わせます。これは、次のオイラーの公式と関連します。これがわかっていれば、双曲線関数の定義を間違えることはないでしょう。

$$
e^{ix}=\cos{x}+i\sin{x},  \cos{x}=\frac{e^{ix}+e^{-ix}}{2},  \sin{x}=\frac{e^{ix}-e^{-ix}}{2}
$$

３．双曲線関数の公式

定義から、以下の公式を導けます。三角関数の公式とほぼ形が同じなのですが、符号が微妙に異なっています。暗記せず、導くほうが安全でしょう。公式 [3] は、他の公式と毛色が異なりますが、実戦で使えます。

公式  [1]　$${\cosh^2{x}-\sinh^2{x}=1}$$
公式  [2]　$${(\cosh{x})'=\sinh{x},  (\sinh{x})'=\cosh{x}}$$
公式  [3]　$${x=\log{(\cosh{x}+\sinh{x})}}$$
公式  [4]　$${\sinh{2x}=2\sinh{x}\cosh{x}}$$
公式  [5]　$${\cosh{2x}=2\cosh^2{x}-1}$$

４．∫√(x^2+a^2)dx

$${a>0}$$ とします。まず、$${\displaystyle \int_{0}^{a}\sqrt{a^2-x^2}dx}$$ を置換積分で計算する方法を確認します。この計算をするには、$${x=a\sin{\theta}}$$ と置換するのでした。

では、次に $${\displaystyle I=\int\sqrt{x^2+a^2}dx}$$ を計算しましょう。

$${y=\sqrt{x^2+a^2}}$$ とします。任意の実数 $${x}$$ について $${x=a\sinh{\theta}}$$ なる実数 $${\theta}$$ が一意的に存在し（これは $${x=a\sinh{\theta}}$$ のグラフを書けばわかる）、これを用いて

$$
\begin{array}{llll} y&=&a\sqrt{\sinh^2{\theta}+1} \\ &=&a\sqrt{\cosh^2{\theta}} &(公式  [1]  より) \\  &=&a\cosh{\theta} &( \cosh{\theta}\geqq0  より) \end{array}
$$

から

　$${I}$$
＝$${\int{y}dx}$$
＝$${\int{a\cosh{\theta}\cdot a\cosh{\theta}d\theta} dx}$$　$${(dx=a\cosh{\theta}d\theta より)}$$
＝$${a^2\int{\cosh^2{\theta}d\theta} }$$

＝$${\dfrac{a^2}{2}\int{(1+\cosh{2\theta})d\theta}　(公式  [5] より) }$$

＝$${\dfrac{a^2}{2}(\theta+\frac{1}{2}\sinh{2\theta})+Const　(公式  [2] より)}$$

＝$${\dfrac{a^2}{2}(\theta+\sinh{\theta}\cosh{\theta})+C　(公式  [4] より) }$$

＝$${\dfrac{a^2}{2}\{\log{(\cosh{\theta}+\sinh{\theta})} +\sinh{\theta}\cosh{\theta}\} +C　(公式  [3] より) }$$

＝$${\dfrac{a^2}{2}\left\{ \log{\left( \dfrac{x}{a}+\dfrac{y}{a} \right)} +\dfrac{x}{a}\cdot\dfrac{y}{a} \right\}+C }$$

＝$${\dfrac{1}{2}\left(xy+a^2\log{\dfrac{x+y}{a}}\right) +C }$$

より、$${C-\dfrac{a^2}{2}\log{a}}$$ を再度 $${C}$$ として

$$
I=\dfrac{1}{2}\{x\sqrt{x^2+a^2}+a^2\log{(x+\sqrt{x^2+a^2})}\} +C
$$

を得ます。$${\displaystyle \int_{0}^{a}\sqrt{a^2-x^2}dx}$$ との類似性に留意しましょう。

この結果から、次のことがわかります。

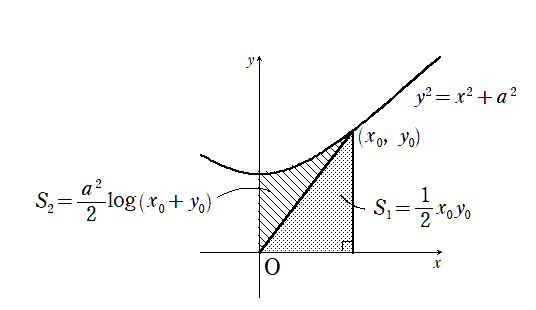
また、$${x}$$ と $${y}$$ を入れ替えると、下の図も得られます。円と双曲線の不思議な関係を味わいましょう。