高校数学　原理を重視する指導例

　ちゃんと原理からわかっていれば不要なのに、公式化・作業化を進めることで、教わる側・教える側ともに理解から遠ざかる事例を、自分は何度も見てきました。「くもわ」などはその典型ですね。高校数学でも、教科書に書いてあるからと言って、それが有益とは限りません。以下、自分の指導例を書いてみます。
　気が向いたら少しずつ加筆します。

たすきがけ

　不要と判断します。係数を比較する習慣のほうが、後々に利いてきます。実践的な問題としては、そもそも「6x^2+5x+4=0 を解け」などのように、有理数範囲で因数分解できない二次式が今後出てきますし、ax^2+bx+c で a が大きい場合（もう少しいうと、整数の積に表す方法が 3 通り以上ある場合）は、解の公式でもいいわけです。

２項の相加平均・相乗平均の不等式の解法

　不要と判断します。呪文の詠唱に時間がかかりすぎますし、以下のように平方完成すれば、自然に解答できます。
　あと、学年が上がったとき、相加相乗を忘れている生徒に、公式を再度説明する手間も面倒なので、こちらで教えます。
　ただし、問題集や参考書には相加相乗で記述されているので、最後の最後に紹介します。

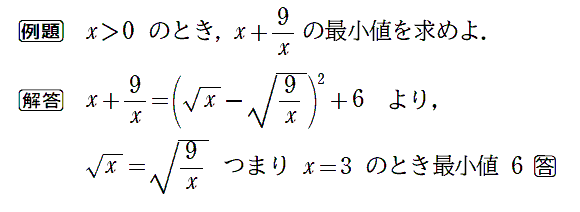
組立除法

　不要と判断します。係数比較で十分です。特に、2x+3 などで割る場合は、わざわざ分数を持ち出す分、損だと思います。

解と係数の関係

　不要と判断します。呪文の詠唱に時間がかかりすぎますし、因数分解と係数比較のほうが、他の問題でも応用が広いです。

三角関数の半角定理

　不要と判断します。倍角定理を変形する方法を教えます。

等差中項・等比中項

　不要と判断します。自分で考えろって、問題投げちゃいます。