
DOBBLEの仕組み解明!(いたさん)
のわっこブログNo.27
ゴールデンウィークが明けて、パルルも再開しました。僕の前回の投稿で、自分のゴールデンウィーク課題を勝手に作り出していました。
なんだかんだほかにもやることが多かったので、なんてことを宣言してしまったんだと2週間前の自分に言ってやりたくもなりました(笑) ですがすきま時間に考えてみて、厳密な証明まではできてしないながら、こうすればDOBBLEを作り出せる、そして実はDOBBLEがこうなっているであろうということまで分かりました。どれだけ興味ある人がいるか分かりませんが、よければお付き合いください。
ドブルがどのようになっているのかは前回のブログを読んでもらえたらと思いますが、ポイントとしては1枚に8つの絵柄が描いてあって全部で55枚あり、どの2枚を取り出しても必ず1つの絵柄が共通していることです。
とはいってもいきなり1枚に8つ絵柄が描かれているものから考えるとサイズ感が大きい話でとっかかりづらいです。ですから最初は1枚に3つ絵柄が描かれている場合だと全部で何枚になるかから考えてみましょう。数学の問題は、まずは具体的で簡単な場合から入ってみると考えやすいですから。

絵柄の1つ1つをA、B、C・・・としていますが、まず1枚目がA・B・Cだとすると次のものは1つの絵柄は同じ、あとはかぶらないようにする必要があります。Aをかぶらせましたが、すると残りの2つは今は新しい絵柄を登場させざるをえないので写真①のようになります。
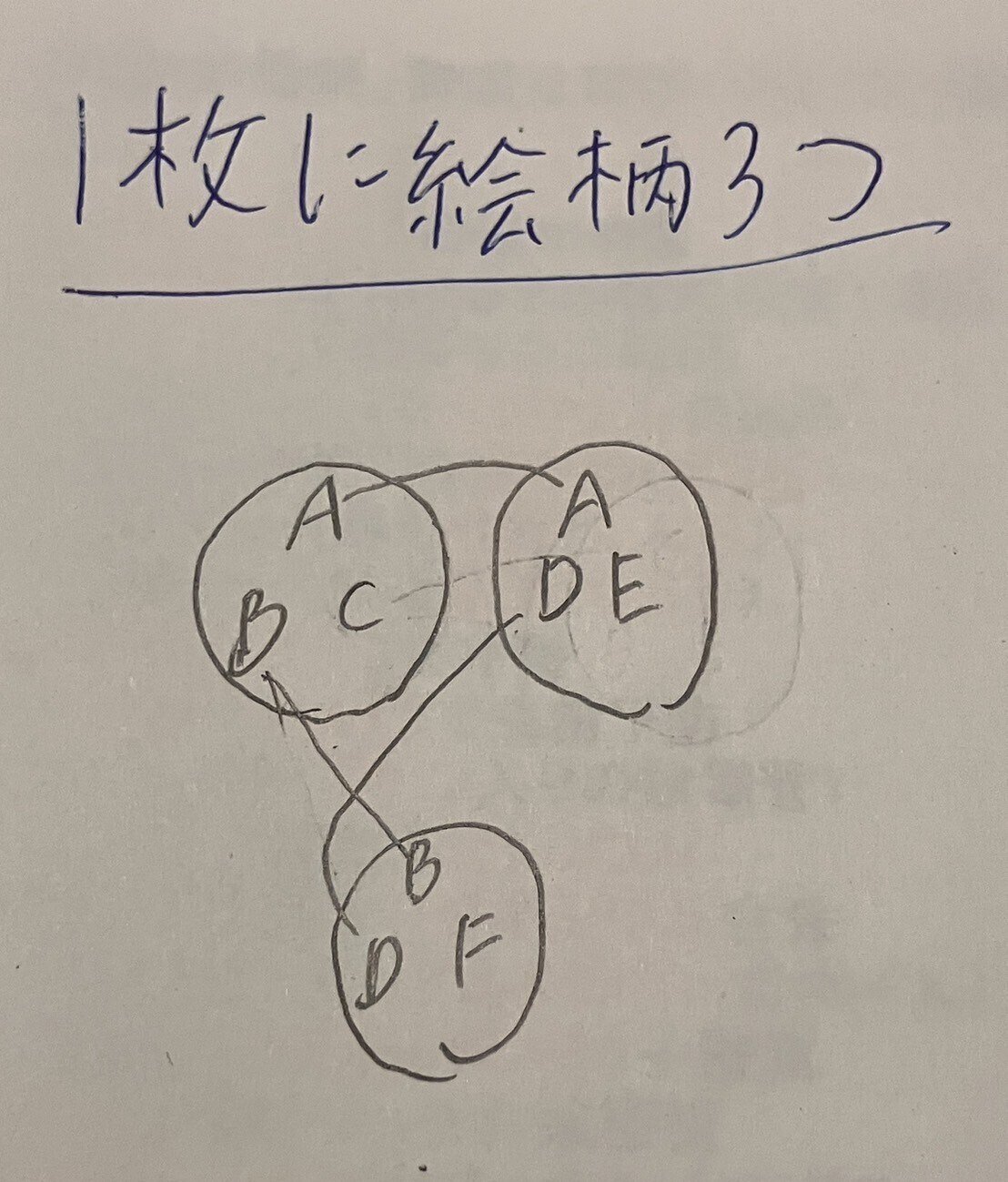
もう1枚増やします。すると写真②のようになります。Aはつながったので、まだ孤立しているBを含めてみます。さらに2枚目とも共通する記号を入れる必要がありますが、ここでAを入れては1枚目と共通するものが2種類になってしまうので適しません。ということでDを入れました。あとは既出のものを入れてしまうと2つ共通してしまうので、新しい絵柄を登場させることになります。
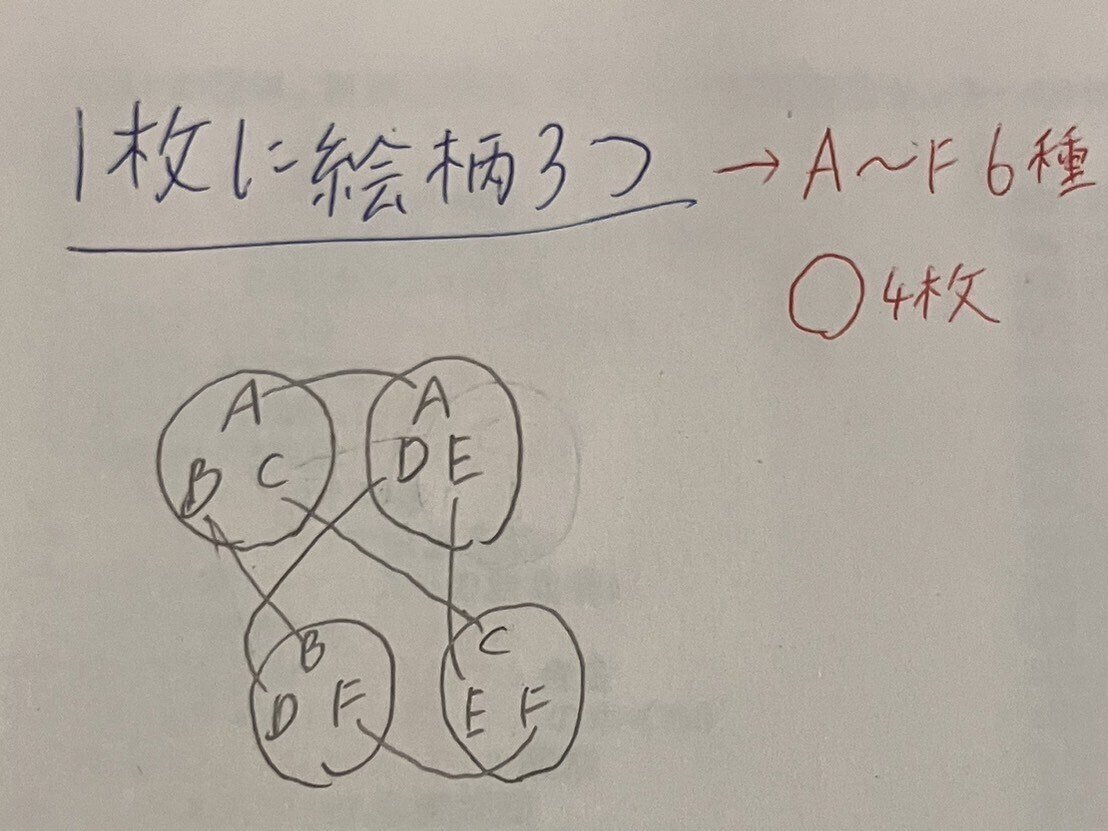
そしてもう1枚、今までのものと1つ共通させるように作ると写真③のようになります。すると全部の絵柄が全部で同じ数ある上にきれいにちょうどつながり合う状態になります。これで1枚絵柄3つ版のDOBBLEの完成です。1枚絵柄3つの場合は6種類の絵柄で4枚作ればできました。

ではひとまわり拡張してみましょう。1枚に絵柄4つです。すると同じように考えていくと写真④ようになります。絵柄は10種類、5枚ということになりました。

さらに1枚絵柄5つも試してみようかというところですが、ちょっとここで数学的に考えてみようと思います。何か規則性はないでしょうか?写真⑤はその過程も書き加えました。種類から考えてみようと思うのですが、1枚の絵柄が3つから4つになって、種類は4つ増えました。ところで、1枚絵柄3つの時に1枚ごとの新しい絵柄が出てきた数を数えてみると順に3→2→1→0となっています。1枚絵柄4つの時には4→3→2→1→0となっています。実は1枚ごとの新しい絵柄の数は、1枚の絵柄の数から1つずつ少なくなって最後は0になっています。絵柄の種類はそれらをすべて足せば出てきます。すると写真⑤のように1枚の絵柄の数がnだとすると、
n(n+1)/2
となります。あ、文字が出てきて頭痛がしてきたという人は読みとばしてください。
一方で枚数は、絵柄3つの時に4枚、絵柄4つの時に5枚と1枚ずつ増えていて分かりやすいですね。まだ2つの場合しかやっていないですが、種類の個数の法則が成り立つことから考えても、1枚の絵柄の数がnの時の枚数については
n+1
となります。
ならば8枚の時が考えられるはずですね。nに8を当てはめてみます。すると絵柄は36種類、枚数は9枚になります。ですがこれ、おかしいのです。最初にも書いたように全部で55枚あるのです。どう考えても枚数が少ないですね。

どうやら今までの考え方では合いそうにないので、1枚絵柄3つの場合をもう1度考えてみます。上で考えたものからさらに枚数を増やせないでしょうか?上の考え方はこれで完結しているので、そこから枚数を増やすには絵柄の種類も増やさなければいけません。ということで7つ目の絵柄を登場させます。さらにそれまでのものと1つは共通させた状態を作りだそうとすると写真⑥のような感じになります。

ですが今度は突然登場した7つ目の絵柄だけ数が少なく不均衡感が否めないですよね。ということで7番目の絵柄が入ったものを増やしてみましょう。このようにするとちょうどどの絵柄も同じ数あり、どのカードも全部つながっている状態が作りだせました。絵柄は6種類から7種類に増え、カードも4枚から7枚に増えました。

さらに1枚絵柄4つも増やしてみます。するとこのように増やすことができました。種類は13、枚数も13です。

ではこの考え方で規則性を見出してみましょう。絵柄4つの時に並べ方を変えていました。この考え方ではこのような感じで考え続けられそうです。1枚の絵柄の数がnの時、絵柄の種類の数も枚数も同じで、
n^2-n+1
と表せそうです。
ではここのnに8を当てはめてみれば今度こそはと意気込んだのですが、計算した結果は57となり55枚とはわずかに合致しませんでした。
とはいえここから2枚なくすと絵柄の総数でいうと16個削ることになるわけで、絵柄の均衡性を保てなくなるように思います。ちなみにおそらくですが、次に少ない枚数で絵柄の均衡が保たれるのは49枚かと思います。
この時点で自分で考えることを諦めました。というのは完全な数学的法則でできていないのではないかと思ったからです。そしてDOBBLEの作られ方について調べてみると、やはり僕と同じように考えた人が何人もいました。そして僕と同じように57という数にたどりついていました。しかし調べた情報の中にゲーム制作者が制作過程についてコメントした記事の内容が紹介されていました。どうやらテストプレイをしたことに加えて、カード作成の機械の都合上でもあったようです。トランプを制作するものと整合性が取れたようです。(52枚+ジョーカー2枚+広告)
となると、自分でDOBBLEを所有しているわけではないので確かめられていませんが、僕の仮説が正しければこのようになっているはずです。57種類ある絵柄のうち14種類はほかより1つ少なく、1種類はさらにもう1つ少なくなっていないでしょうか。
ということで、僕のゴールデンウィークの自由研究発表でした~
のわ / パルル?全然関係ありません←
▼今回の投稿者について

いたさん(板倉匡利(まさとし))
パルルを知ってからのわのいろんなことを目の当たりしてきて半年、お留守番をするまでになりました。
毎週木曜日の16時頃からパルルで子どもの勉強を見たりもしています~。
最近、歩くサードプレイスになりつつあると感じています。
「楽しさの中に学びがある」を大切に生きています。
X:https://twitter.com/Masa0808R
Facebook:https://www.facebook.com/masatosi.itakura
インスタ:https://www.instagram.com/masatoshi_itakura/
Threads:https://www.threads.net/@masatoshi_itakura
ブログ:https://itasan-kibunyasan.hatenablog.com/
▼のわについて
のわ [人と人の繋がりを通して、新しい暮らしを考える]
3つの取り組みをしています。
・イベントのわ〈ライブ、ワークショップ、ごはん会など、人の集まる場の開催〉
・新栄のわ〈新しい働き方、暮らし方を提案するコミュニティースペースの運営〉
・チャンネルのわ〈音楽やアート、身近な問題について動画を制作しyoutube で配信〉
