FANG＋と組み合わせを考える

サブテーマ：最強指数FANG＋一択リスクを緩和するには？！

１　初めに

　最近、ポートフォリオ最適化に関する記事を書いていく中、過去実績ではFANG＋インデックスが、リータンだけでなく投資効率の１つの指標であるシャープレシオでも優秀であることがわかってきました。
　今回はこのFANG＋インデックス１００％では安心して夜が眠れない人（自分含め）に、他のアセットとの組み合わせ比率を調査してみます。
正直なところ結論のコードだけで概要はわかるのですが、今回の調査過程を見てもらう方が、投資リテラシー向上にもPYTHONでできることの把握にも良いと考えますので、ご興味があればぜひ見てください。

今回の結論：過去10年間での比較
比較対象：株式　SP500（SPY）、NASDAQ100（QQQ）
　　　　　債権　AGG（債券全般）、TLT（長期米国債）
　　　　　金　　GLD
　リターン重視：FANG＋100％　　　　（年率28％、リスク25％）
　バランス重視：FANG＋70％：金30%　（年率21％、リスク18％）

---

最適化ポートフォリオ実行後

FANG＋と各アセットと割合とのリターンVSリスク（標準偏差）

---

知人よりプログラム部分が難しくてよくわからないとご指摘をいただきました。そのためこのチャンネルでは、PYTHONを使った米国株投資に関わるさまざまな調査の結果OUTPUTにこだわった記事にします。投資に関わる身近な疑問にも答えていきますので、投資リテラシー向上にお役立ちを目指します！！
　なお、全ての解析データは引き続き、PYTHONを活用してコード全文も掲載します。Googleコラボならまずは”コピペ”でチャレンジできます。これから勉強始めたい方にも、プログラミングで何ができるのかを知る良いチャンスとなればと思っていますので応援お願いします！！

---

２　豆知識

１）投資信託：FANG＋インデックスとは？

【特集】iFreeNEXT FANG+インデックス| 大和アセットマネジメント株式会社

　この記事のでのFANG＋とは、大和アセットマネジメントから販売されている下記の１０社に均等投資するFANG＋株価指数に連動する投資信託（つみたてNISA対象）です。前回と同じリンクを再度掲載しておきます。

３　実践

１）調査内容

　今回、FANG＋とそれぞれアセットを組み合わせた場合のリスクVSリターンの変化と、トレンドをそれぞれ確認していきます。全て同じコードでティッカーを変更して実行しています。
　調査期間はFANG＋インデックスが2014年からデータとなりますのでその期間として10年間の集計となります。
　その他組み合わせ指数はいずれも日本国内で買える米国ETFを使用しています。対象ティッカーは下記の通りです。
　SPY：S&P500、QQQ：NASDAQ100、AGG：債券全般、TLT：長期米国債、GLD：金

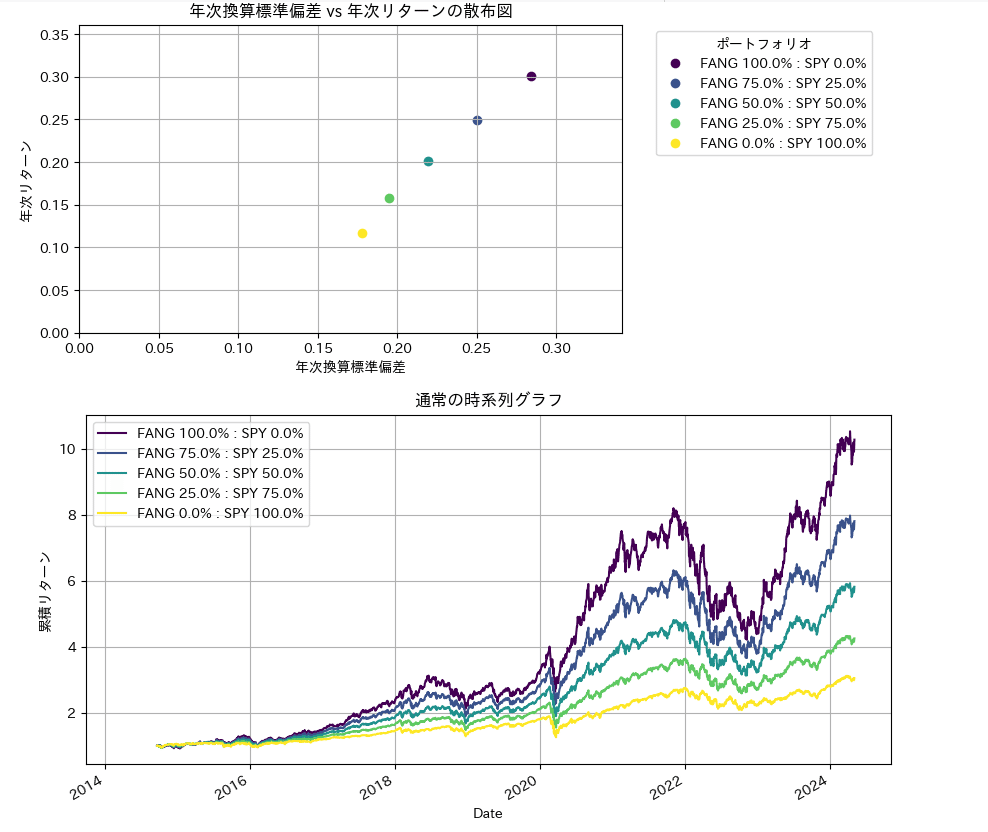
２）各種データのリターンVSリスク、時系列プロット

①長期米国債（TLT）
　実行結果は下記の通りです。最後に相関係数も示しますが、TLTは株式とは逆相関の傾向があります。TLTの配分を増やすほどリターンは下がりますが、時系列プロットを確認すると、100％では暴落時に下落幅が抑えられていることがわかります。この傾向は過去の記事で紹介したS&P500と同じであり、FANG＋インデックスでも債券は株価下落の幅を低減させることができています。

pip install japanize-matplotlib
import yfinance as yf
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import japanize_matplotlib  # 日本語表示に対応

# 対象のティッカーシンボル
tickers = ['^NYFANG', 'TLT']

# データの取得
data = yf.download(tickers, start="2014-04-01", end=pd.Timestamp.now().strftime('%Y-%m-%d'))['Adj Close']

# ティッカーの順序を正確に指定
data = data[['^NYFANG', 'TLT']]

# ウェイトを定義
weights = [(1.0, 0.0), (0.75, 0.25), (0.5, 0.5), (0.25, 0.75), (0.0, 1.0)]
portfolio_metrics = pd.DataFrame()
portfolio_time_series = pd.DataFrame(index=data.index)

# 各ウェイトに基づいてポートフォリオラベルのリストを生成
portfolio_labels = [f"FANG {weight[0]*100}% : TLT {weight[1]*100}%" for weight in weights]

# リスクフリーレートの設定
risk_free_rate = 0.01

# 各ポートフォリオに対して計算を実行
for weight in weights:
    portfolio_label = f"FANG {weight[0]*100}% : TLT {weight[1]*100}%"

    # 月次リターンの計算
    returns = data.pct_change().dot(weight)
    cum_returns = (1 + returns).cumprod()
    cum_returns.iloc[0] = 1  # 最初のNaNを補完
    portfolio_time_series[portfolio_label] = cum_returns

    # 年次リターン
    annual_returns = (1 + returns).resample('Y').prod() - 1
    avg_annual_return = annual_returns.mean()

    # 年次換算標準偏差
    annual_std = returns.std() * np.sqrt(252)

    # 最大ドローダウンの計算
    rolling_max = cum_returns.cummax()
    drawdown = (cum_returns - rolling_max) / rolling_max
    max_drawdown = drawdown.min()

    # シャープレシオの計算
    sharpe_ratio = (returns.mean() * 252 - risk_free_rate) / annual_std

    # 結果の保存
    portfolio_metrics[portfolio_label] = [avg_annual_return, annual_std, max_drawdown, sharpe_ratio]

# データフレームの列をこのラベルリストに基づいて順序付け
portfolio_metrics = portfolio_metrics[portfolio_labels]
portfolio_time_series = portfolio_time_series[portfolio_labels]

# メトリクスのインデックス名を設定
portfolio_metrics.index = ['年次リターン', '年次換算標準偏差', '最大ドローダウン', 'シャープレシオ']

# カラーマップを生成
colors = cm.viridis(np.linspace(0, 1, len(portfolio_labels)))  # グラデーションカラーマップ生成

# 散布図をプロット
plt.figure(figsize=(7, 4))
for idx, label in enumerate(portfolio_labels):
    annual_return = portfolio_metrics.loc['年次リターン', label]
    annual_std_dev = portfolio_metrics.loc['年次換算標準偏差', label]
    plt.scatter(annual_std_dev, annual_return, color=colors[idx], label=label)

plt.xlabel('年次換算標準偏差')
plt.ylabel('年次リターン')
plt.title('年次換算標準偏差 vs 年次リターンの散布図')
plt.legend(title="ポートフォリオ", bbox_to_anchor=(1.05, 1), loc='upper left')
plt.grid(True)

# 軸の範囲を動的に調整
max_std = portfolio_metrics.loc['年次換算標準偏差'].max() * 1.2
max_return = portfolio_metrics.loc['年次リターン'].max() * 1.2
plt.xlim(0, max_std)
plt.ylim(0, max_return)

# 対数スケールに変換
y_values = [50, 100, 200, 300, 400, 500, 1000]
log_y_values = np.log10(y_values)

# 時系列グラフのプロット
fig, axes = plt.subplots(2, 1, figsize=(9, 9))

# 通常の時系列グラフ
colors = cm.viridis(np.linspace(0, 1, len(portfolio_labels)))  # グラデーションカラーマップ生成
portfolio_time_series.plot(ax=axes[0], color=colors)
axes[0].set_title('通常の時系列グラフ')
axes[0].set_ylabel('累積リターン')
axes[0].grid(True)

# スタートを100に固定し対数軸メモリ
normalized_portfolio = portfolio_time_series.divide(portfolio_time_series.iloc[0]) * 100
log_portfolio = np.log10(normalized_portfolio.replace(0, np.nan).dropna())
log_portfolio = log_portfolio[portfolio_labels]  # 正しい順序で再割り当て

log_portfolio.plot(ax=axes[1], color=colors)
axes[1].set_title('対数スケールの正規化された時系列グラフ（開始値を100に設定）')
axes[1].set_ylabel('インデックス化されたリターン(対数スケール)')
axes[1].set_yticks(log_y_values)  # Y軸のメモリ位置を設定
axes[1].set_yticklabels(y_values)  # Y軸のメモリラベルを設定
axes[1].grid(True)
plt.tight_layout()
plt.show()

# メトリクス表示（後で実行する部分）
#print(portfolio_metrics)

②金とFANG＋
　同様にGLDと同じように実行した結果を示します。（コードは省略）
金もTLTと同様な傾向で、割合が増えるほど下落幅は小さくなります。ただ金の方が最終的なリターンが高い傾向も見えます。

③債券（AGG）とFANG＋
　同様に債券全般であるAGGで同じ調査をすると混ぜるほどリターンはさがります。債券の一部である会社が発行する社債は、株価大きな下落局面では同様に下がるため組み合わせ相手として意味は見出せません。

④S&P500との比較
　続けて株式同士を組み合わせた場合です。こちらもAGGと同じ傾向ですが、例えFANG＋インデックスを組み合わせなくても、年率10％のリターンが見込めます。どれぐらいFANG＋インデックスを組み合わせるのかは、結局個人の期待リターンと許容できるリスクに応じてとしての結果となります。（QQQとも同じ結果ですのでそちらも省略しますが、興味のある方はGoogle Colabでコピペ＋コード部分の修正で実行できますのでみてみてください。）

３）集計して一覧で確認

これまでの個別で組み合わせを確認してきましたが、一度にリスクvsリターンの図で表示させます。

import yfinance as yf
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import japanize_matplotlib  # 日本語表示に対応

# 対象のティッカーペア
asset_pairs = [('^NYFANG', 'AGG'), ('^NYFANG', 'TLT'), ('^NYFANG', 'GLD'), ('^NYFANG', 'QQQ'), ('^NYFANG', 'SPY')]

# ウェイトを定義
weights = [(1.0, 0.0), (0.75, 0.25), (0.5, 0.5), (0.25, 0.75), (0.0, 1.0)]

# リスクフリーレートの設定
risk_free_rate = 0.01

# カラーマップを生成
colors = cm.viridis(np.linspace(0, 1, len(asset_pairs) * len(weights)))

# 散布図用の全体図を初期化
plt.figure(figsize=(10, 6))

# 全ての結果を格納するデータフレーム
all_portfolio_metrics = pd.DataFrame()

color_idx = 0
for pair in asset_pairs:
    # データの取得
    tickers = list(pair)
    data = yf.download(tickers, start="2014-10-01", end=pd.Timestamp.now().strftime('%Y-%m-%d'))['Adj Close']
    data = data[list(pair)]  # ティッカーの順序を正確に指定

    portfolio_metrics = pd.DataFrame()
    portfolio_time_series = pd.DataFrame(index=data.index)

    # 各ウェイトに基づいてポートフォリオラベルのリストを生成
    portfolio_labels = [f"{pair[0]} {weight[0]*100}% : {pair[1]} {weight[1]*100}%" for weight in weights]

    # 各ポートフォリオに対して計算を実行
    for weight, label in zip(weights, portfolio_labels):
        # 月次リターンの計算
        returns = data.pct_change().dot(weight)
        cum_returns = (1 + returns).cumprod()
        cum_returns.iloc[0] = 1  # 最初のNaNを補完
        portfolio_time_series[label] = cum_returns

        # 年次リターン
        annual_returns = (1 + returns).resample('Y').prod() - 1
        avg_annual_return = annual_returns.mean()

        # 年次換算標準偏差
        annual_std = returns.std() * np.sqrt(252)

        # 最大ドローダウンの計算
        rolling_max = cum_returns.cummax()
        drawdown = (cum_returns - rolling_max) / rolling_max
        max_drawdown = drawdown.min()

        # シャープレシオの計算
        sharpe_ratio = (returns.mean() * 252 - risk_free_rate) / annual_std

        # 結果の保存
        portfolio_metrics[label] = [avg_annual_return, annual_std, max_drawdown, sharpe_ratio]
        plt.scatter(annual_std, avg_annual_return, color=colors[color_idx], label=label)
        color_idx += 1

     # メトリクスのインデックス名を設定し、相関係数を追加
    portfolio_metrics.index = ['年次リターン', '年次換算標準偏差', '最大ドローダウン', 'シャープレシオ']
    all_portfolio_metrics = pd.concat([all_portfolio_metrics, portfolio_metrics], axis=1)


# 散布図のレイアウト設定
plt.xlabel('年次換算標準偏差')
plt.ylabel('年次リターン')
plt.title('ポートフォリオ リスクリターン散布図')
plt.legend(title="ポートフォリオ", bbox_to_anchor=(1.05, 1), loc='upper left')
plt.grid(True)
plt.show()

# 全ての結果をテーブルとして表示
print(all_portfolio_metrics)

次に、FANG+と各アセットの割合について線グラフで表示させます。線グラフで表示することで傾向が良く見えると思っていただけると思います。

import matplotlib.pyplot as plt

# グラフ設定
fig, ax1 = plt.subplots(figsize=(10, 6))

# リターンのプロット（左軸）
colors = ['b', 'g', 'r', 'c','Black']  # 色設定
asset_types = ['AGG', 'TLT', 'GLD', 'QQQ', 'SPY']  # 資産の種類
for idx, asset in enumerate(asset_types):
    x = [100, 75, 50, 25, 0]  # ウェイト比率（SPYの比率）
    y_return = [all_portfolio_metrics[f"^NYFANG {w}.0% : {asset} {100-w}.0%"]['年次リターン'] for w in x]
    ax1.plot(x, y_return, label=f'{asset} リターン', color=colors[idx], marker='o')

ax1.set_xlabel('SPYのウェイト比率 (%)')
ax1.set_ylabel('年次リターン', color='b')
ax1.tick_params(axis='y', labelcolor='b')
ax1.grid(True)
ax1.set_ylim(-0.20, 0.40)  # リターンの軸範囲を設定

# 標準偏差のプロット（右軸）
ax2 = ax1.twinx()  # 共有X軸の第二Y軸を生成
for idx, asset in enumerate(asset_types):
    y_std = [all_portfolio_metrics[f"^NYFANG {w}.0% : {asset} {100-w}.0%"]['年次換算標準偏差'] for w in x]
    ax2.plot(x, y_std, label=f'{asset} 標準偏差', color=colors[idx], linestyle='--', marker='x')

ax2.set_ylabel('年次換算標準偏差', color='r')
ax2.tick_params(axis='y', labelcolor='r')
ax2.set_ylim(0.00, 0.5)  # 標準偏差の軸範囲を設定

# 凡例の表示、グラフの右外に配置
lines1, labels1 = ax1.get_legend_handles_labels()
lines2, labels2 = ax2.get_legend_handles_labels()
ax2.legend(lines1 + lines2, labels1 + labels2, loc='upper left', bbox_to_anchor=(1.05, 1), title='ポートフォリオ')

plt.title('FANGと他資産のリターンと標準偏差の比較')
plt.show()


# グラフ設定
fig, ax1 = plt.subplots(figsize=(10, 6))

# シャープレシオのプロット（左軸）
colors = ['b', 'g', 'r', 'c','Black']  # 色設定
asset_types = ['AGG', 'TLT', 'GLD', 'QQQ', 'SPY']  # 資産の種類
for idx, asset in enumerate(asset_types):
    x = [100, 75, 50, 25, 0]  # ウェイト比率（SPYの比率）
    y_sharpe = [all_portfolio_metrics[f"^NYFANG {w}.0% : {asset} {100-w}.0%"]['シャープレシオ'] for w in x]
    ax1.plot(x, y_sharpe, label=f'{asset} シャープレシオ', color=colors[idx], marker='o')

ax1.set_xlabel('FNAGのウェイト比率 (%)')
ax1.set_ylabel('シャープレシオ', color='b')
ax1.tick_params(axis='y', labelcolor='b')
ax1.grid(True)
# シャープレシオの範囲を設定する場合
ax1.set_ylim(0, 1.2)  # 例えば 0 から 1 の範囲

# 最大ドローダウンのプロット（右軸）
ax2 = ax1.twinx()  # 共有X軸の第二Y軸を生成
for idx, asset in enumerate(asset_types):
    y_drawdown = [all_portfolio_metrics[f"^NYFANG {w}.0% : {asset} {100-w}.0%"]['最大ドローダウン'] for w in x]
    ax2.plot(x, y_drawdown, label=f'{asset} 最大ドローダウン', color=colors[idx], linestyle='--', marker='x')

ax2.set_ylabel('最大ドローダウン', color='r')
ax2.tick_params(axis='y', labelcolor='r')
# 最大ドローダウンの範囲を設定する場合
ax2.set_ylim(-0.6, 0.6)  # 例えば -0.6 から 0 の範囲

# 凡例の表示、グラフの右外に配置
lines1, labels1 = ax1.get_legend_handles_labels()
lines2, labels2 = ax2.get_legend_handles_labels()
ax2.legend(lines1 + lines2, labels1 + labels2, loc='upper left', bbox_to_anchor=(1.2, 1), title='ポートフォリオ')

plt.title('SPYと他資産のシャープレシオと最大ドローダウンの比較')
plt.show()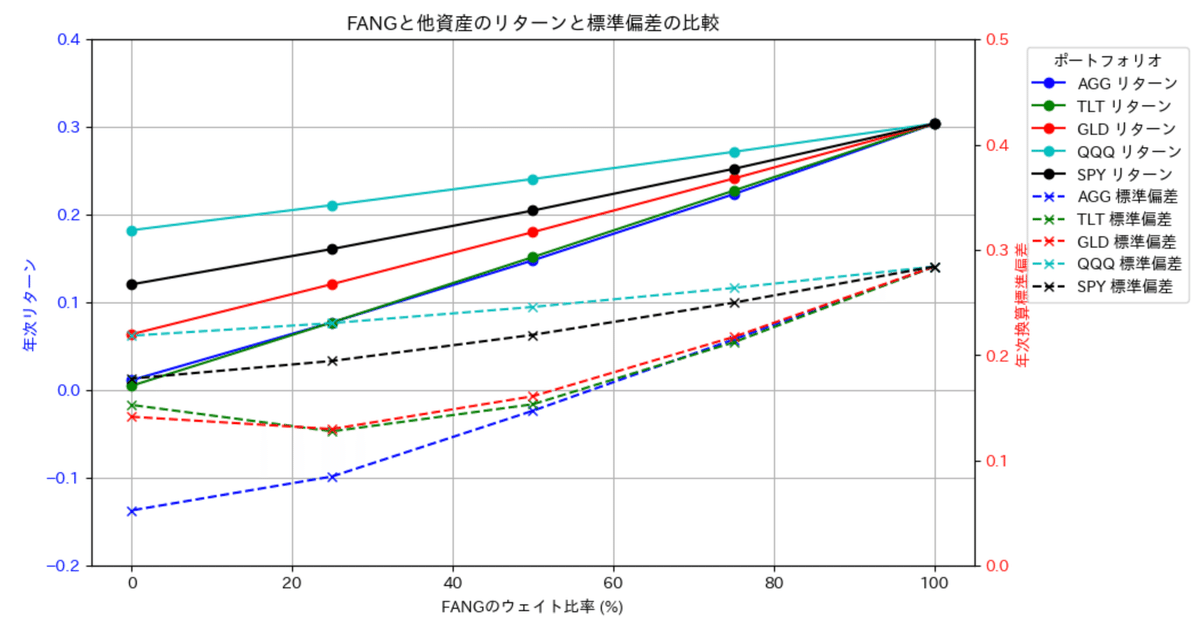

FANG＋と各アセット割合変更した場合のリスクVSリターン

FANG＋と各アセット割合変更した場合のシャープレシオと最大ドローダウン

それぞれ横軸をウェイト比率（％）とし、２軸でそれぞれの指標を図示しました。結局のところリターンはFANG＋100％に勝てるものはなく、混ぜることでリターンが減少していることがわかります。
その傾向はリスクも最大ドローダウンも同じなのですが、唯一GLDはシャープレシオがFANG＋100％の場合より改善する傾向が見えます。

以上、これまでの各調査をまとめたグラフを作成し図示してみました。こうすることで、FANG＋と各アセットの挙動の違いが比較しやすくなったのではないでしょうか？ご興味のある組み合わせがあれば、ぜひトライしてみてください。

４）効率化フォンティア曲線と、ポートフォリオ最適化

最後に、効率化フロンティア曲線と最適なポートフォリオについて計算させます。同時に相関係数も出力し、各アセットとの相関係数上の比較も実施します。

!pip install PyPortfolioOpt

import yfinance as yf
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import japanize_matplotlib  # 日本語表示に対応
from pypfopt import expected_returns, risk_models, EfficientFrontier, plotting


# 対象のティッカーシンボル
tickers = [ 'SPY', 'TLT', 'GLD', 'AGG','QQQ','^NYFANG']

# データの取得
data = yf.download(tickers, start="2014-10-01", end=pd.Timestamp.now().strftime('%Y-%m-%d'))['Adj Close']

# 年化された期待リターンの計算
mean_returns = expected_returns.mean_historical_return(returns, frequency=12)

# 日次リターンの計算
daily_returns = data.pct_change()

# FANGに対する相関係数を計算
correlations = daily_returns.corr().loc['^NYFANG']

# 月次リターンの計算
monthly_data = data.resample('M').last()
monthly_returns = monthly_data.pct_change().dropna()

# 年化された期待リターンとリスク（共分散行列）の計算
mean_returns = expected_returns.mean_historical_return(monthly_data, frequency=12)
cov_matrix = risk_models.sample_cov(monthly_data, frequency=12)

# 各ティッカーのリスク（標準偏差）とリターンの計算
individual_risks = np.sqrt(np.diag(cov_matrix))
individual_returns = mean_returns.values

# 最適化：シャープレシオを最大化
ef = EfficientFrontier(mean_returns, cov_matrix)
weights = ef.max_sharpe()
cleaned_weights = ef.clean_weights()

# 最適化されたポートフォリオのパフォーマンス計算
expected_return, volatility, sharpe_ratio = ef.portfolio_performance(verbose=True)

# 効率的フロンティアの点を生成
ef_new = EfficientFrontier(mean_returns, cov_matrix)
fig, ax = plt.subplots(1, 3, figsize=(18, 6))

# 散布図と効率的フロンティア
ax[0].scatter(volatility, expected_return, color='red', s=100, label='最適化されたポートフォリオ')
ax[0].scatter(individual_risks, individual_returns, color='blue', s=50)  # 各ティッカー
for i, txt in enumerate(mean_returns.index):
    ax[0].annotate(txt, (individual_risks[i], individual_returns[i]))
plotting.plot_efficient_frontier(ef_new, ax=ax[0], show_assets=True)

ax[0].set_title('ポートフォリオおよび各ティッカーのリスクとリターン')
ax[0].set_xlabel('標準偏差（リスク）')
ax[0].set_ylabel('期待リターン')
ax[0].grid(True)
ax[0].legend()

# ウェイトの棒グラフ
ax[1].bar(cleaned_weights.keys(), cleaned_weights.values(), color='green')
ax[1].set_title('ポートフォリオの最適化されたウェイト')
ax[1].set_xlabel('資産')
ax[1].set_ylabel('ウェイト')
ax[1].grid(True)

# FANGとの相関係数の棒グラフ
correlation_values = correlations.drop('^NYFANG')  # FANG自体の相関は除外
ax[2].bar(correlation_values.index, correlation_values.values, color='purple')
ax[2].set_title('FANGとの相関係数')
ax[2].set_xlabel('資産')
ax[2].set_ylabel('相関係数')
ax[2].grid(True)

plt.tight_layout()
plt.show()

左）効率化フロンティア&シャープレシオ最大化　中）最適化時の保有割合　右）相関係数vsFANG

これまでの調査は、上記の効率化フロンティア曲線図に集約されています。
結論：
　リターン重視：FANG＋100％　　　　（年率28％、リスク25％）
　バランス重視：FANG＋70％：金30%　（年率21％、リスク18％）

結局、FANG＋100％のリスクを抑えるには金を投資するのがベストとの結論でした。相関係数では反対な動きをするTLTですが、この２年間の長期金利の高騰故の債券安の影響で、リスクとリターンに優れるGLDとの組み合わせが良いという結論に繋がったものと考えます。

４　まとめ

　今回は、FANG＋との組み合わせを泥臭く調査してみました。FANG＋と金投資で過去10年実績では年率20％かつ最大ドローダウンを抑えた投資ができていたことがわかります。例えFANG＋インデックスではなくても、S&P500で年率10％のリターンでした。どれぐらいFANG＋インデックスを組み合わせるのかは、結局個人の期待リターンと許容できるリスクに応じてとしての結果となります。
　今後も同じ傾向が続くとは言えませんが、FANG＋銘柄が伸びない時にはS&P500もそれほど増えないし、金が暴落するような自体があればそれこそ世界の終わりのような気もしますので、100％真似する必要はありませんが、頭の片隅に置いておこうと思ったのが今回の結果です。
皆様の投資生活のお役に立てれば幸いです。

＊今回の結果も、過去１０年の実績をもとにシミュレーションした結果です。今後の結果を保証するものではありません。実際の投資判断はご自身にてお願いいたします。

---

以下、過去記事、AI時系列予測等のご紹介
他サイトですがココならで、A I（LSTM）を使った株価予測の販売もやってます。こちらではFREDから、失業率や２年１０年金利、銅価格等結果も取得しLSTMモデルで予測するコードとなってますので興味があれば見てみてください。またその他２件も米国株投資とは直接関係はありませんがプログラム入門におすすめですのでみてみてください。

APPLE（変更可）米株価予測コード販売します AI・LSTMモデルで5日後を予測するpythonコード | 株式・各種投資の相談 | ココナラ

機械学習・重回帰分析　おすすめプログラム販売します 散布図（回帰式、相関係数、P値）・重回帰分析（特徴量評価） | 機械学習 | ココナラ

機械学習LightGBM コード販売します Deep Learning, 特徴量解析，SHAP値 | 機械学習 | ココナラ

---

チャンネル紹介：Kota＠Python＆米国株投資チャンネル

Kota＠Python＆米国株投資チャンネル｜note

過去の掲載記事：興味があればぜひ読んでください。
グラフ化集計の基礎：S &P500と金や米国債を比較してます。

移動平均を使った時系列予測

---