レバレッジ投資を分析する

サブテーマ：レバナス（QLD）、TQQQの一括・積立シミュレーション　　

１　初めに

　今回は、新NISAでは買えない商品ですが、良い意味でも悪い意味でも話題のNASDAQ100のレバレッジ商品について分析します。
　レバレッジとは価格変動が、２倍、３倍となる商品であり、投資信託のリターンランキング（下落局面ではマイナス側で）で良く目にすると思います。また単純に暴落時にはその２倍、３倍の価値が目減りするだけでなく、同じ価格変動を繰り返すだけで価値が減る低減と呼ばれている現象もあります。
今回は怖い怖いでは終わらず、過去右肩あがりの優秀な指数であるNASDAQ100の２倍、３倍レバレッジ商品ならどれぐらいのリスクとリターンがあるのかをPYTHONで分析、シミュレーションしてみます。
　レバレッジ商品について興味のある方に参考になると思いますので、ぜひお付き合いください。

　今回のゴール：①年次リターン、リスクの計算

各レバレッジ商品のリターンとリスク

　今回のゴール：②1000回シミュレーションによるリータンの可視化

一括投資＋分割投資５年後のリターン【上段左：S＆P500　右：NASAQ100、
下段左：NASDAQ100✖️２倍（QLD）、右：NASDAQ100✖️３倍（TQQQ）】

---

知人よりプログラム部分が難しくてよくわからないとご指摘をいただきました。そのためこのチャンネルでは、PYTHONを使った米国株投資に関わるさまざまな調査の結果OUTPUTにこだわった記事にします。投資に関わる身近な疑問にも答えていきますので、投資リテラシー向上にお役立ちを目指します！！
　なお、全ての解析データは引き続き、PYTHONを活用してコード全文も掲載します。Googleコラボならまずはコピペで実行し、ティッカーや期間などの簡単な変更からチャレンジできます。これから勉強始めたい方にも、プログラミングで何ができるのかを知る良いチャンスとなればと思っていますので応援お願いします！！

---

２　豆知識

１）レバレッジとは

　レバレッジ投資信託やレバレッジETFは、投資対象のリターンを一定の倍率で増幅させることを目指す金融商品です。例えば、ある指数の日々のリターンを2倍にするレバレッジETFがある場合、その指数が1%上昇した日は、ETFは理論上2%のリターンを目指します。しかし、このメカニズムは損失にも同様に作用し、リスクが高まります。レバレッジETFを利用することで大きなリターンを目指すことができますが、その反面、大きな損失を被る可能性もあるため、慎重な検討が必要です。

２）低減とは

　レバレッジ商品における横ばい相場での基準価格の低減効果とは、市場が小さな上昇と下降を繰り返す横ばい相場では、レバレッジETFはこれらの小さな動きを拡大して反映します。その際、例えば、ある日に市場が5%下落した後、同じ5%上昇すると、元の価値に戻るわけではありません。100円が5%下落すると95円になり、その後5%上昇しても99.75円にしかなりません。この原理がレバレッジによって強調され、結果として横ばい相場でもETFの価値が徐々に減少していくことになります。

３　実践

１）調査内容

　今回、NASDAQ100のレバレッジ無：QQQ、２倍：QLD、３倍＊TQQQのETFと比較としてS &P500に連動するETF：SPYの過去１０年間実際の値動きから、年率としたリターンとリスク（標準偏差）を計算します。
なお、通称レバナスとは、２倍レバレッジの投資信託のことをさしており、QLDと同じ価格の変化です。厳密にはQLDは為替ヘッジがなく、若干の手数料の差がありますが基本同じ値動きです。（手数料のシミュレーションは前回記事参照）
　今回は、年率のリターンとリスクから投資額600（円またはドル）として５年間の投資をシミュレーションします。シミュレーションは過去の記事と同様にモンテカルロシミュレーションの技法を用い1000回実施したときのリターンの分布をヒストグラムで表示させることで可視化します。
　一括投資：　　　元本600万円を一度に購入し５年間保有
　分割投資：　　　元本600万円を10万円／月づつ５年間購入
　一括投資・分割投資：　元本300万円を一括で購入後、
　　　　　　　　　　　10万円／月づつ５年間購入

２）リスクとリターンの算出

いつものようにYahoo Financeから株価データを取得し、月毎のデータに変換します。今回月々の変化を年毎のリータンに変換しその中央値を年率リターンとしています。またリスクも同様に年率に換算しています。

import yfinance as yf
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib  # 日本語表示に対応

# 対象のティッカーシンボル
tickers = ['SPY', 'QQQ', 'QLD', 'TQQQ']

ticker_colors = {
    'SPY': 'red',
    'QQQ': 'green',
    'QLD': 'blue',
    'TQQQ': 'cyan'
}

# データの取得
data = yf.download(tickers, start="2010-03-01", end=pd.Timestamp.now().strftime('%Y-%m-%d'))
# 必要な列のみ抽出
data = data['Adj Close']

# 月次リターンを計算
monthly_returns = data.resample('M').ffill().pct_change()

# 月次リターンから年次リターンを計算（累積積を使用）
cumulative_annual_returns = (1 + monthly_returns).resample('A').prod() - 1

# 月次リターンの標準偏差を計算
monthly_std_devs = monthly_returns.std()

# 年率換算標準偏差は既に月次リターンに基づいているため、そのまま使用
annualized_std_devs_from_monthly = monthly_std_devs * np.sqrt(12)

# 結果をDataFrameに格納（累積積に基づく年次リターンを使用）
results = pd.DataFrame({
    "年次リターン": cumulative_annual_returns.median(),  # 年次リターンの中央値
    "月次リターンに基づく年率換算標準偏差": annualized_std_devs_from_monthly
})


# 散布図をプロット
plt.figure(figsize=(10, 6))

# results DataFrameをループして、各ティッカーのポイントをプロット
for i, (index, row) in enumerate(results.iterrows()):
    # トレンドグラフで定義した色を使用
    color = ticker_colors.get(index, 'gray')  # ティッカーに色が割り当てられていない場合は'gray'を使用
    plt.scatter(row["年次リターン"], row["月次リターンに基づく年率換算標準偏差"], color=color, label=index)
    plt.annotate(index, (row["年次リターン"], row["月次リターンに基づく年率換算標準偏差"]))

# 軸のラベルを設定
plt.xlabel('年次リターン')
plt.ylabel('月次リターンに基づく年率換算標準偏差')

# 軸の範囲を設定
x_max = results["年次リターン"].max() * 1.5
y_max = results["月次リターンに基づく年率換算標準偏差"].max() * 1.5
plt.xlim(0, x_max)
plt.ylim(0, y_max)

# グラフのタイトルを設定
plt.title('年次リターン vs 年率換算標準偏差')

# グリッドを表示
plt.grid(True)

# 凡例を表示
plt.legend()

plt.show()

各レバレッジ商品のリターンとリスク

実際に散布図にプロットした結果が上になります。
QQQ、QLD(2倍）,TQQQ（３倍）がほぼ直線に並んでいます。これは要は見込めるリターンはレバレッジ比率に応じて大きく見込めるものの、その程度に比例してリスク（標準偏差）もその分大きくなることを示してます。
　また実際の価格変動のグラフも対数軸メモリでプロットすると下記の通りでレバレッジ比率に応じて、リターンは大きくなっているものの、その分下落時の変化も大きな割合となっていることがわかります。

リターン・リスクの元データ（対数プロット&2010年3月1日を100として正規化）

３）一括・積立・一括＋積立　それぞれのリターンシミュレーション

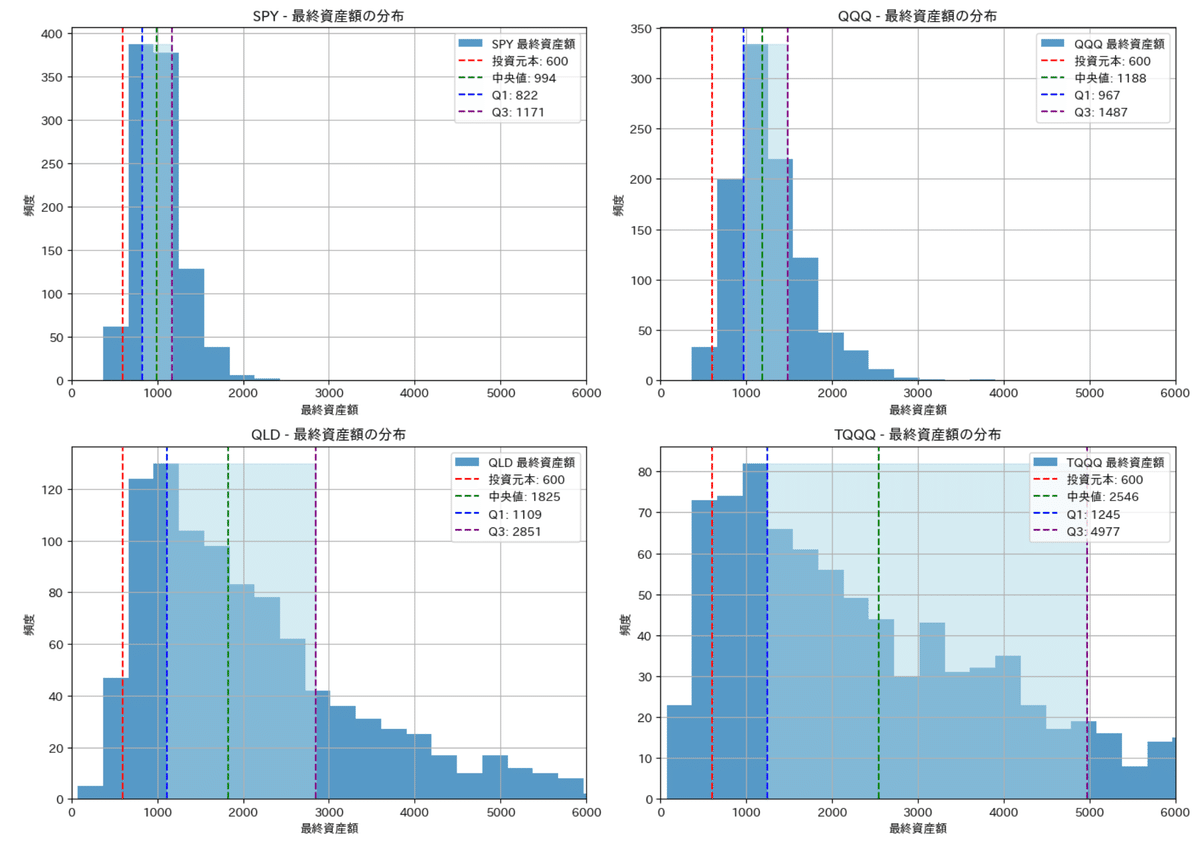
実際にこれらを先ほど計算した年率のリターンとリスクの値を使ってそれぞれ1000回シミュレーションし、その1000回のデータをヒストグラムにプロットした結果を下記に示します。ヒストグラムの頻度はその区間にある数で頻度が50であれば1000回中50回がそのリターンであったことを示してます。またそれぞれに、元本（600万円）に対し、中央値、Q 1点（下位２５％）、Q3点（７５％点）を線引きしています。
　実際のコードは下記で、600万円を一括投資、分割投資、一括＋分割投資で金額を変更しシミュレーションを実施しています。（コードは一括投資の場合です。）

import numpy as np
import matplotlib.pyplot as plt

# パラメータ設定
initial_investment = 600  # 初期投資額
monthly_investment = 0  # 月次積立額
investment_duration = 60  # 投資期間（月）
simulations = 1000  # シミュレーション回数

# シミュレーションの実行と結果の収集
all_final_values = []

for ticker in tickers:
    # 既存のコードから月次リターンの平均と標準偏差を取得
    monthly_return_mean = monthly_returns[ticker].mean()
    monthly_return_std = monthly_std_devs[ticker]
    final_values = np.zeros(simulations)

    for simulation in range(simulations):
        total_value = initial_investment
        for month in range(investment_duration):
            monthly_return = np.random.normal(monthly_return_mean, monthly_return_std)
            total_value += monthly_investment
            total_value = total_value * (1 + monthly_return)
        final_values[simulation] = total_value
    all_final_values.append(final_values)

# 全シミュレーション結果からビンの範囲を決定するための配列を生成
flat_all_final_values = [value for sublist in all_final_values for value in sublist]
min_value = min(flat_all_final_values)
max_value = max(flat_all_final_values)
bins = np.linspace(min_value, max_value, 500)  # binsの数を500に設定

# 投資元本の計算（初期投資額 + 月次積立投資額の合計）
total_investment = initial_investment + monthly_investment * investment_duration
# x_maxをシミュレーション結果の最大値を基に設定
#x_max = max_value * 1.1  # 最大値の110%をX軸の最大値とする
x_max = total_investment*10

# 2x2のグリッドでサブプロットを作成し、X軸の範囲を設定
fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(14, 10))
axes = axes.flatten()

for i, ticker in enumerate(tickers):
    ax = axes[i]
    ticker_final_values = all_final_values[i]
    
    median_value = np.median(ticker_final_values)
    Q1 = np.percentile(ticker_final_values, 25)
    Q3 = np.percentile(ticker_final_values, 75)
    
    # ヒストグラムをプロット
    n, bins, patches = ax.hist(ticker_final_values, bins=bins, alpha=0.75, label=f'{ticker} 最終資産額')
    
    # Q1からQ3の間を透明な色で塗りつぶす
    ax.fill_betweenx([0, max(n)], Q1, Q3, color='lightblue', alpha=0.5)
    
    # 投資元本、中央値、Q1、Q3の線を追加
    ax.axvline(x=total_investment, color='r', linestyle='--', label=f'投資元本: {total_investment:.0f}')
    ax.axvline(x=median_value, color='green', linestyle='--', label=f'中央値: {median_value:.0f}')
    ax.axvline(x=Q1, color='blue', linestyle='--', label=f'Q1: {Q1:.0f}')
    ax.axvline(x=Q3, color='purple', linestyle='--', label=f'Q3: {Q3:.0f}')

    ax.set_title(f'{ticker} - 最終資産額の分布')
    ax.set_xlabel('最終資産額')
    ax.set_ylabel('頻度')
    ax.legend()
    ax.grid(True)
    ax.set_xlim(0, x_max)

plt.tight_layout()
plt.show()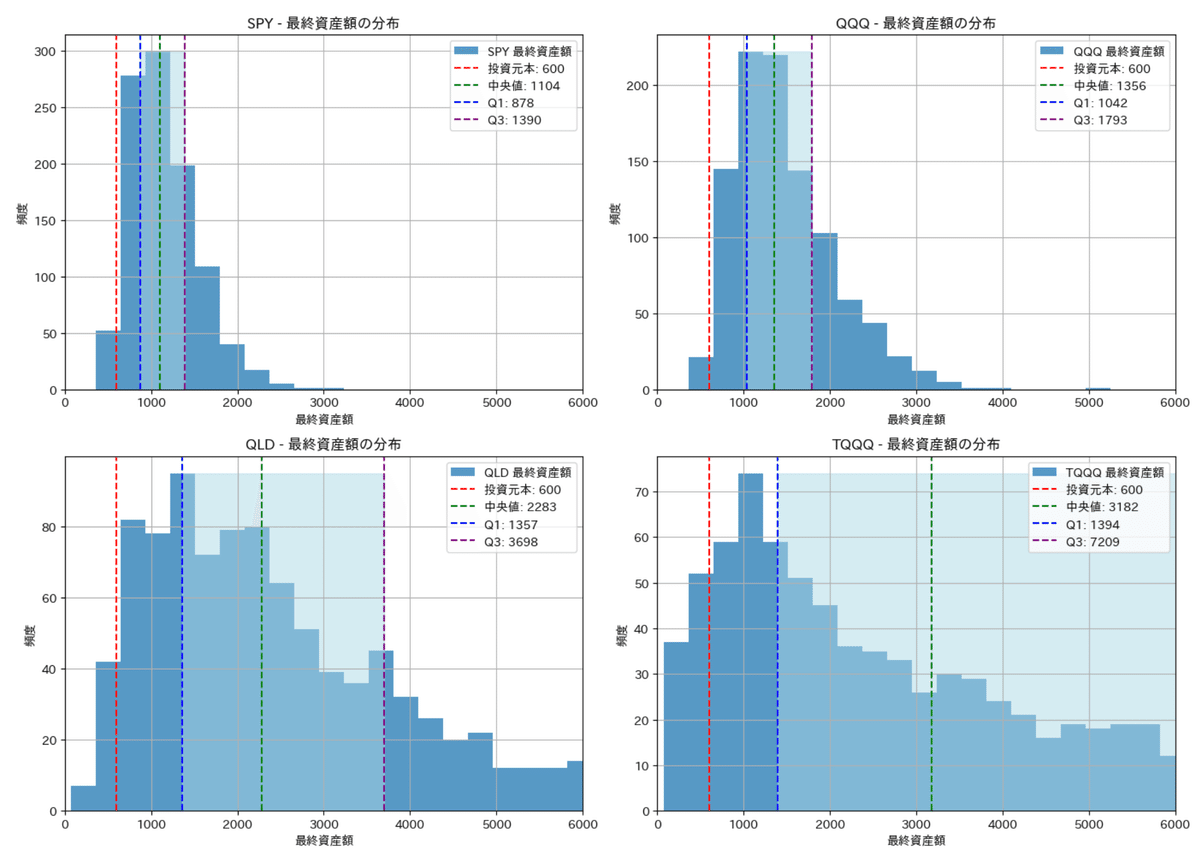

一括投資の場合

分割投資の場合

一括投資＋分割投資の場合

　いずれも同じ傾向であり、レバレッジのないSPYやQQQは元本割れの確率は低く、想定リターンの通り中央値は５年後には２倍弱のリターンが見込めてます。レバレッジがあると、まず元本割れの確率が上がりますが、それ以上にリターンの中央値が３倍、４倍へと高くなり、Q 1点の２５％以上（＝４回に３回）は、２倍レバレッジでも、１倍レバレッジのQQQの中央値と同程度です。

４）考察

　考察として２倍レバレッジのQLD（＝レバナス相当）の３条件を抜き取ってみました。一番リターンが良いのは一括投資です。ヒストグラムでも右側の傾きが穏やかであり、５０％以上の確率ではありますが、たった５年で５倍以上のリターンが得られる可能性があることを示しています。逆に分散投資であれば、元本割れの確率が一番少なくなっています。大きくマイナスになり得る頻度は100回に2回以下の確率であり、かつQ 1（25％）でも1.５倍のリターンが得られそうであることを示してます。
　このリスクとリターンの間をとったような条件が、半分を一括投資で、残り半分を積立購入した場合です。この条件であれば、リスクも分割投資と同程度ながら、リターンも中央値で３倍以上となかなか魅力的な購入方法であることがわかります。レバレッジ商品の買い方の参考になれば幸いです。

NASDAQ100 ２倍レバレッジ（QLD）の投資方法別リターン（各５年）

４　まとめ

　今回レバレッジ商品のリターンとリスクを深掘りしてみました。この結果ではレバレッジ商品の方が魅力的に見えてしまうのではないでしょうか？（嘘ではないが、良いところを切り取ってしまった可能性もあり得ます）
　これは調査対象とした2010年からのNASDAQ100指数が確実な右肩あがりであるゆえであり、過去の傾向が未来も続くとは言えませんが、今後も技術の発展が続く限り同じような未来がないわけでもないと言えるのではないでしょうか。なおレバレッジ商品のリスクは暴落時です。資産が５０％以上の減少も結構頻繁に起きています。今回の結果では少なくとも５年保持したら過去１０年超の傾向と同程度のリターンが見込めますので、下がったと時に売ってしまわない覚悟がある人、もしくは証券口座を見ない人には、余剰資産の一部で、自分が信頼できる銘柄や指数があるのであれば、その株価やその指数に連動するレバレッジ商品を買っておくのも悪くはないのかもしれません。皆様の投資方針の参考になれば幸いです。

---

以下、過去記事、AI時系列予測等のご紹介

他サイトですがココならで、A I（LSTM）を使った株価予測の販売もやってます。こちらではFREDから、失業率や２年１０年金利、銅価格等結果も取得しLSTMモデルで予測するコードとなってますので興味があれば見てみてください。またその他２件も米国株投資とは直接関係はありませんがプログラム入門におすすめですのでみてみてください。

APPLE（変更可）米株価予測コード販売します AI・LSTMモデルで5日後を予測するpythonコード | 株式・各種投資の相談 | ココナラ

機械学習・重回帰分析　おすすめプログラム販売します 散布図（回帰式、相関係数、P値）・重回帰分析（特徴量評価） | 機械学習 | ココナラ

機械学習LightGBM コード販売します Deep Learning, 特徴量解析，SHAP値 | 機械学習 | ココナラ

---

チャンネル紹介：Kota＠Python＆米国株投資チャンネル

Kota＠Python＆米国株投資チャンネル｜note

過去の掲載記事：興味があればぜひ読んでください。
グラフ化集計の基礎：S &P500と金や米国債を比較してます。

移動平均を使った時系列予測

---

５　全コード　＊ぜひコピペでトライ！！

実行環境Google Colab 　＊Googleアカウントがあれば無料で使えます。

import yfinance as yf
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib  # 日本語表示に対応

# 対象のティッカーシンボル
tickers = ['SPY', 'QQQ', 'QLD', 'TQQQ']

ticker_colors = {
    'SPY': 'red',
    'QQQ': 'green',
    'QLD': 'blue',
    'TQQQ': 'cyan'
}

# データの取得
data = yf.download(tickers, start="2010-03-01", end=pd.Timestamp.now().strftime('%Y-%m-%d'))
# 必要な列のみ抽出
data = data['Adj Close']

# 月次リターンを計算
monthly_returns = data.resample('M').ffill().pct_change()

# 月次リターンから年次リターンを計算（累積積を使用）
cumulative_annual_returns = (1 + monthly_returns).resample('A').prod() - 1

# 月次リターンの標準偏差を計算
monthly_std_devs = monthly_returns.std()

# 年率換算標準偏差は既に月次リターンに基づいているため、そのまま使用
annualized_std_devs_from_monthly = monthly_std_devs * np.sqrt(12)

# 結果をDataFrameに格納（累積積に基づく年次リターンを使用）
results = pd.DataFrame({
    "年次リターン": cumulative_annual_returns.median(),  # 年次リターンの中央値
    "月次リターンに基づく年率換算標準偏差": annualized_std_devs_from_monthly
})

# DataFrameを表示
results

#１　時系列の線グラフを描画
plt.figure(figsize=(14, 7))  # グラフのサイズを設定
# 各ティッカーについて線グラフをプロット、ここで色を適用
for ticker in tickers:
    plt.plot(data[ticker], label=ticker, color=ticker_colors[ticker])  
plt.title('月次調整終値')
plt.xlabel('日付')
plt.ylabel('調整終値')
plt.legend()

# 基準日の価格で各ティッカーの価格を割り、100をかけてインデックス化
normalized_data = data.apply(lambda x: x / x.iloc[0] * 100)

#２　インデックス化されたデータの時系列グラフを描画
plt.figure(figsize=(14, 7))
for ticker in tickers:
    plt.plot(normalized_data[ticker], label=ticker, color=ticker_colors[ticker])  
plt.axhline(y=100, color='red', linestyle='--', linewidth=1)
plt.title('正規化された月次調整終値')
plt.xlabel('日付')
plt.ylabel('正規化価格')
plt.legend()

#３　対数軸のグラフの描写
plt.figure(figsize=(14, 7))
for ticker in tickers:
    plt.plot(normalized_data[ticker], label=ticker, color=ticker_colors[ticker])  
plt.axhline(y=100, color='red', linestyle='--', linewidth=1)
plt.title('対数目盛りでの正規化された月次調整終値')
plt.xlabel('日付')
plt.ylabel('対数正規化価格')
plt.legend()
plt.yscale('log')

plt.show()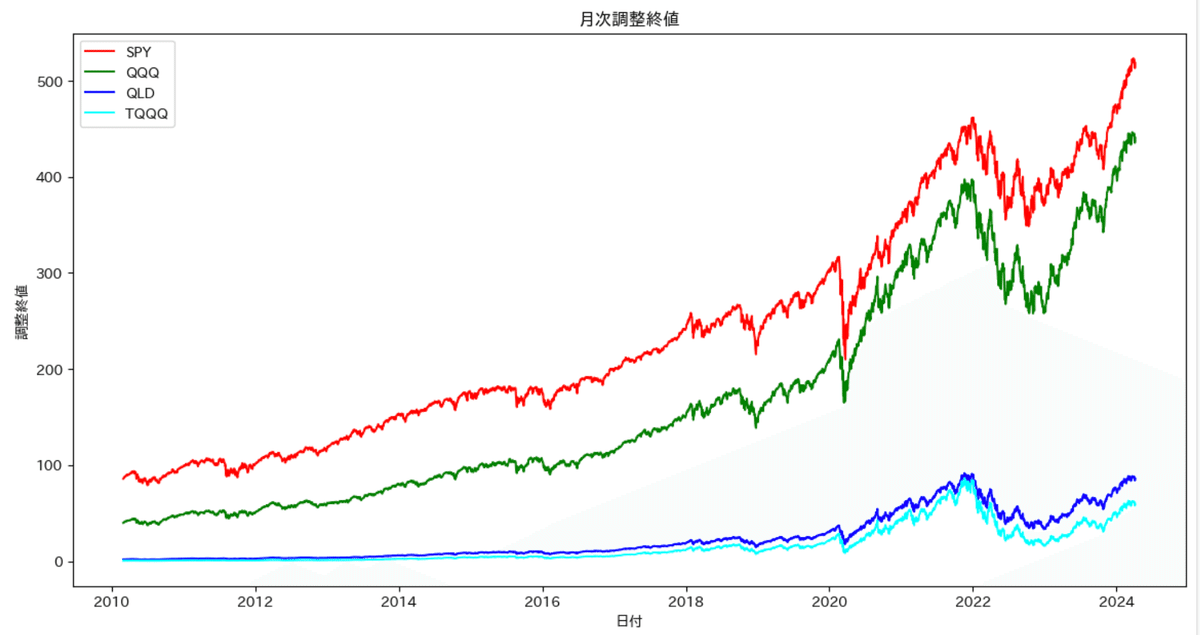

# 散布図をプロット
plt.figure(figsize=(10, 6))

# results DataFrameをループして、各ティッカーのポイントをプロット
for i, (index, row) in enumerate(results.iterrows()):
    # トレンドグラフで定義した色を使用
    color = ticker_colors.get(index, 'gray')  # ティッカーに色が割り当てられていない場合は'gray'を使用
    plt.scatter(row["年次リターン"], row["月次リターンに基づく年率換算標準偏差"], color=color, label=index)
    plt.annotate(index, (row["年次リターン"], row["月次リターンに基づく年率換算標準偏差"]))

# 軸のラベルを設定
plt.xlabel('年次リターン')
plt.ylabel('月次リターンに基づく年率換算標準偏差')

# 軸の範囲を設定
x_max = results["年次リターン"].max() * 1.5
y_max = results["月次リターンに基づく年率換算標準偏差"].max() * 1.5
plt.xlim(0, x_max)
plt.ylim(0, y_max)

# グラフのタイトルを設定
plt.title('年次リターン vs 年率換算標準偏差')

# グリッドを表示
plt.grid(True)

# 凡例を表示
plt.legend()

plt.show()

import numpy as np
import matplotlib.pyplot as plt

# パラメータ設定
initial_investment = 600  # 初期投資額
monthly_investment = 0  # 月次積立額
investment_duration = 60  # 投資期間（月）
simulations = 1000  # シミュレーション回数

# シミュレーションの実行と結果の収集
all_final_values = []

for ticker in tickers:
    # 既存のコードから月次リターンの平均と標準偏差を取得
    monthly_return_mean = monthly_returns[ticker].mean()
    monthly_return_std = monthly_std_devs[ticker]
    final_values = np.zeros(simulations)

    for simulation in range(simulations):
        total_value = initial_investment
        for month in range(investment_duration):
            monthly_return = np.random.normal(monthly_return_mean, monthly_return_std)
            total_value += monthly_investment
            total_value = total_value * (1 + monthly_return)
        final_values[simulation] = total_value
    all_final_values.append(final_values)

# 全シミュレーション結果からビンの範囲を決定するための配列を生成
flat_all_final_values = [value for sublist in all_final_values for value in sublist]
min_value = min(flat_all_final_values)
max_value = max(flat_all_final_values)
bins = np.linspace(min_value, max_value, 500)  # binsの数を500に設定

# 投資元本の計算（初期投資額 + 月次積立投資額の合計）
total_investment = initial_investment + monthly_investment * investment_duration
# x_maxをシミュレーション結果の最大値を基に設定
#x_max = max_value * 1.1  # 最大値の110%をX軸の最大値とする
x_max = total_investment*10

# 2x2のグリッドでサブプロットを作成し、X軸の範囲を設定
fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(14, 10))
axes = axes.flatten()

for i, ticker in enumerate(tickers):
    ax = axes[i]
    ticker_final_values = all_final_values[i]
    
    median_value = np.median(ticker_final_values)
    Q1 = np.percentile(ticker_final_values, 25)
    Q3 = np.percentile(ticker_final_values, 75)
    
    # ヒストグラムをプロット
    n, bins, patches = ax.hist(ticker_final_values, bins=bins, alpha=0.75, label=f'{ticker} 最終資産額')
    
    # Q1からQ3の間を透明な色で塗りつぶす
    ax.fill_betweenx([0, max(n)], Q1, Q3, color='lightblue', alpha=0.5)
    
    # 投資元本、中央値、Q1、Q3の線を追加
    ax.axvline(x=total_investment, color='r', linestyle='--', label=f'投資元本: {total_investment:.0f}')
    ax.axvline(x=median_value, color='green', linestyle='--', label=f'中央値: {median_value:.0f}')
    ax.axvline(x=Q1, color='blue', linestyle='--', label=f'Q1: {Q1:.0f}')
    ax.axvline(x=Q3, color='purple', linestyle='--', label=f'Q3: {Q3:.0f}')

    ax.set_title(f'{ticker} - 最終資産額の分布')
    ax.set_xlabel('最終資産額')
    ax.set_ylabel('頻度')
    ax.legend()
    ax.grid(True)
    ax.set_xlim(0, x_max)

plt.tight_layout()
plt.show()

import numpy as np
import matplotlib.pyplot as plt

# パラメータ設定
initial_investment = 0  # 初期投資額
monthly_investment = 10  # 月次積立額
investment_duration = 60  # 投資期間（月）
simulations = 1000  # シミュレーション回数

# シミュレーションの実行と結果の収集
all_final_values = []

for ticker in tickers:
    # 既存のコードから月次リターンの平均と標準偏差を取得
    monthly_return_mean = monthly_returns[ticker].mean()
    monthly_return_std = monthly_std_devs[ticker]
    final_values = np.zeros(simulations)

    for simulation in range(simulations):
        total_value = initial_investment
        for month in range(investment_duration):
            monthly_return = np.random.normal(monthly_return_mean, monthly_return_std)
            total_value += monthly_investment
            total_value = total_value * (1 + monthly_return)
        final_values[simulation] = total_value
    all_final_values.append(final_values)

# 全シミュレーション結果からビンの範囲を決定するための配列を生成
flat_all_final_values = [value for sublist in all_final_values for value in sublist]
min_value = min(flat_all_final_values)
max_value = max(flat_all_final_values)
bins = np.linspace(min_value, max_value, 120) 

# 投資元本の計算（初期投資額 + 月次積立投資額の合計）
total_investment = initial_investment + monthly_investment * investment_duration
# x_maxをシミュレーション結果の最大値を基に設定
#x_max = max_value * 1.1  # 最大値の110%をX軸の最大値とする
x_max = total_investment*10

# 2x2のグリッドでサブプロットを作成し、X軸の範囲を設定
fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(14, 10))
axes = axes.flatten()

for i, ticker in enumerate(tickers):
    ax = axes[i]
    ticker_final_values = all_final_values[i]
    
    median_value = np.median(ticker_final_values)
    Q1 = np.percentile(ticker_final_values, 25)
    Q3 = np.percentile(ticker_final_values, 75)
    
    # ヒストグラムをプロット
    n, bins, patches = ax.hist(ticker_final_values, bins=bins, alpha=0.75, label=f'{ticker} 最終資産額')
    
    # Q1からQ3の間を透明な色で塗りつぶす
    ax.fill_betweenx([0, max(n)], Q1, Q3, color='lightblue', alpha=0.5)
    
    # 投資元本、中央値、Q1、Q3の線を追加
    ax.axvline(x=total_investment, color='r', linestyle='--', label=f'投資元本: {total_investment:.0f}')
    ax.axvline(x=median_value, color='green', linestyle='--', label=f'中央値: {median_value:.0f}')
    ax.axvline(x=Q1, color='blue', linestyle='--', label=f'Q1: {Q1:.0f}')
    ax.axvline(x=Q3, color='purple', linestyle='--', label=f'Q3: {Q3:.0f}')

    ax.set_title(f'{ticker} - 最終資産額の分布')
    ax.set_xlabel('最終資産額')
    ax.set_ylabel('頻度')
    ax.legend()
    ax.grid(True)
    ax.set_xlim(0, x_max)

plt.tight_layout()
plt.show()

import numpy as np
import matplotlib.pyplot as plt

# パラメータ設定
initial_investment = 300  # 初期投資額
monthly_investment = 5  # 月次積立額
investment_duration = 60  # 投資期間（月）
simulations = 1000  # シミュレーション回数

# シミュレーションの実行と結果の収集
all_final_values = []

for ticker in tickers:
    # 既存のコードから月次リターンの平均と標準偏差を取得
    monthly_return_mean = monthly_returns[ticker].mean()
    monthly_return_std = monthly_std_devs[ticker]
    final_values = np.zeros(simulations)

    for simulation in range(simulations):
        total_value = initial_investment
        for month in range(investment_duration):
            monthly_return = np.random.normal(monthly_return_mean, monthly_return_std)
            total_value += monthly_investment
            total_value = total_value * (1 + monthly_return)
        final_values[simulation] = total_value
    all_final_values.append(final_values)

# 全シミュレーション結果からビンの範囲を決定するための配列を生成
flat_all_final_values = [value for sublist in all_final_values for value in sublist]
min_value = min(flat_all_final_values)
max_value = max(flat_all_final_values)
bins = np.linspace(min_value, max_value, 500)  # binsの数を500に設定

# 投資元本の計算（初期投資額 + 月次積立投資額の合計）
total_investment = initial_investment + monthly_investment * investment_duration
# x_maxをシミュレーション結果の最大値を基に設定
#x_max = max_value * 1.1  # 最大値の110%をX軸の最大値とする
x_max = total_investment*10

# 2x2のグリッドでサブプロットを作成し、X軸の範囲を設定
fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(14, 10))
axes = axes.flatten()

for i, ticker in enumerate(tickers):
    ax = axes[i]
    ticker_final_values = all_final_values[i]
    
    median_value = np.median(ticker_final_values)
    Q1 = np.percentile(ticker_final_values, 25)
    Q3 = np.percentile(ticker_final_values, 75)
    
    # ヒストグラムをプロット
    n, bins, patches = ax.hist(ticker_final_values, bins=bins, alpha=0.75, label=f'{ticker} 最終資産額')
    
    # Q1からQ3の間を透明な色で塗りつぶす
    ax.fill_betweenx([0, max(n)], Q1, Q3, color='lightblue', alpha=0.5)
    
    # 投資元本、中央値、Q1、Q3の線を追加
    ax.axvline(x=total_investment, color='r', linestyle='--', label=f'投資元本: {total_investment:.0f}')
    ax.axvline(x=median_value, color='green', linestyle='--', label=f'中央値: {median_value:.0f}')
    ax.axvline(x=Q1, color='blue', linestyle='--', label=f'Q1: {Q1:.0f}')
    ax.axvline(x=Q3, color='purple', linestyle='--', label=f'Q3: {Q3:.0f}')

    ax.set_title(f'{ticker} - 最終資産額の分布')
    ax.set_xlabel('最終資産額')
    ax.set_ylabel('頻度')
    ax.legend()
    ax.grid(True)
    ax.set_xlim(0, x_max)

plt.tight_layout()
plt.show()