
FANG+指数の最適レバレッジ比率
1 初めに
あけましておめでとうございます。今年もよろしくお願いします!!
今回は、過去、1年での投資信託のうち、3番目にランクインしているレバレッジファングプラス。レバレッジのかかった投資信託に興味があるひとにはきいたことがあるだろう、最適なレバレッジ比率について、FANG+の場合を調べてみました。初心者の投資には向かない投資商品ですが、少額積立してみるには面白い商品だと思います。ぜひお付き合いください。
Youtube始めました。最近Youtubeに注力しているため、こちらがおろそかになっています。しかし、投資に役立つ、面白いコード、知見ができたらこちらでも紹介していきます。Youtubeチャンネルともども、今年もよろしくお願いします!!(Pythonコードより解析結果に興味のある人にはYoutubeがおすすめです。)
今回のまとめ


2 豆知識
1)最適なレバレッジ比率とは?
最適なレバレッジ比率とは、市場の期待リターン(μ)とボラティリティ(σ)に基づき決定される指標です。理論上は、レバレッジ倍率 k=μ/σ2 で表され、過度に大きいレバレッジはボラティリティの影響が増幅し、リスクが高まります。一般には1.5倍から2倍程度が長期投資に適した一つの目安とされますが、市場環境や投資期間、手数料、金利などの条件によって最適値は変動します。ボラティリティが低くリターンが安定している場合は、やや高いレバレッジが有効になることもありますが、乱高下が激しい局面では急激なドローダウンに注意が必要です。自分のリスク許容度や運用スタイルに合わせ、慎重に設定することが重要です。
2)マネックス証券 値上がり率ランキング
1,2はSP500の投資信託のレバレッジ商品です。SP500の最適レバレッジ比率も気になりますので、後ほど紹介します。

https://fund.monex.co.jp/rankinglist
3 実践
1)最適なレバレッジ比率計算
縦軸リターン、横軸をレバレッジ比率とした場合図で、最大となる点が、その指数での最適なレバレッジ比率となります。今回のFANG+指数設定されたのは、2014年夏であるため、2015年1月からの実績をもとに最適なレバレッジ比率を計算した結果がこちらです。
なお1つだけの指数で比較できないため、レバナス等で有名なNASDAQ100指数、ランキングを独占しているS&P500指数の最適レバレッジ比率を出力させました。なお、こちらの2つは、1990年からのデータとしています。調査期間は違いますが、データは多い方が参考となると思いますので、注意して確認してもらえればと思います。

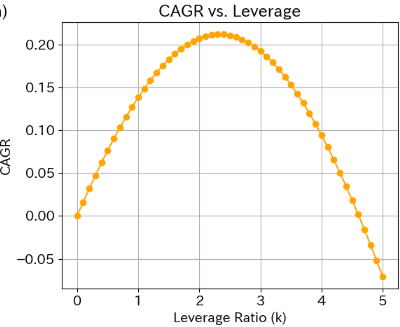

その結果、FANG+は3.79と非常に高い最適なレバレッジ比率です。
比較としたNASDAQ100は2.34倍、S&P500は2.96倍でした。先ほどのランキング1位の4倍はあまり効率的ではないもの、3倍はこの計算からだと効率がよさそうです。
2)最適比率でのリターン
FANG+の最適レバレッジ比率で保持していたときのリターンです。もとの1倍でもランキング上位の成績にもかかわらず、横ばっているぐらいのリターンです。具体的な金額でいえば、ちょうど10年前に、ファングプラス3.79倍の商品があったとして、投資していたとすると、340倍、340万円です。10万円なら3千万越え、100万円なら3億です。注意点は、2022年以降の下げ相場等に耐えれるかどうかです。2億円が、2千万円になるような下落にたえれるかどうかは、普通の人には無理だとも思えます。

参考まで、1990年までのNASDAQ100とSP500の最適比率でのリターンの状況です。こちらも長期すぎてよくわからなくなっていますが、コードは掲載しておきますので、お好みのティッカーや指数で実行してみるのも面白いと思います。


4 最後に
今回は、最適なレバレッジ比率を調査するコードを紹介してみました。本部でも触れましたが、お好みのティッカーや指数でこのコードを実行してみるのも面白いのではと思います。なお、Youtubeチャンネルでは、このようなコード使った、投資に役立つ情報を配信していきたいと思っていますので、そちらもぜひ見てみてください。
記事の感想、要望があれば下記X(旧Twitterまで)
*今後の記事に活用させていただきます!!
Youtube
以下、過去記事、AI時系列予測等のご紹介
他サイトですがココならで、A I(LSTM)を使った株価予測の販売もやってます。こちらではFREDから、失業率や2年10年金利、銅価格等結果も取得しLSTMモデルで予測するコードとなってますので興味があれば見てみてください。またその他2件も米国株投資とは直接関係はありませんがプログラム入門におすすめです。
チャンネル紹介:Kota@Python&米国株投資チャンネル
過去の掲載記事:興味PYがあればぜひ読んでください。
グラフ化集計の基礎:S &P500と金や米国債を比較してます。
移動平均を使った時系列予測
以下実行コード:コピペで実行してみてください。
## 最適レバレッジ比率してトレンド描画
import yfinance as yf
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import datetime
# ---------------------------
# 1. データの取得
# ---------------------------
# 取得期間を設定(例:2015年以降)
start_date = "1990-01-01"
end_date = datetime.date.today().strftime("%Y-%m-%d")
# yfinance を用いてFANG+指数(^NYFANG)のデータをダウンロード
df = yf.download('^GSPC', start=start_date, end=end_date)
# 日次の終値(Adj Close)が無い場合は Close を使用することも可
# 本コードでは、Adj Close を優先使用
df = df[['Adj Close']].dropna()
# ---------------------------
# 2. 日次リターン・ボラティリティの算出
# ---------------------------
# 日次リターン(%)を計算
df['Daily_Return'] = df['Adj Close'].pct_change()
# μ: 日次リターンの平均, σ: 日次リターンの標準偏差
mu = df['Daily_Return'].mean() # 平均
sigma = df['Daily_Return'].std() # 標準偏差
# ---------------------------
# 3. 理論的な最適レバレッジ k = μ / σ^2
# ---------------------------
optimal_k = mu / (sigma ** 2)
print(f"理論的な最適レバレッジ倍率 (k) = {optimal_k:.3f}")
# ---------------------------
# 4. レバレッジポートフォリオのパフォーマンス計算
# ---------------------------
# ここではシンプルに「日次リターン × レバレッジ倍率」で計算する想定
# 実際のレバレッジETFはボラティリティやコストなどの影響も複雑に反映しますが、
# 今回は簡易的に理論値の効果を確認するためのサンプルです。
# 4-1. レバレッジなし(k=1)の場合の累積リターン(ベンチマーク)
df['Cumulative_1x'] = (1 + df['Daily_Return']).cumprod()
# 4-2. 理論最適レバレッジ(k)を適用した場合の累積リターン
df['Leveraged_Return'] = df['Daily_Return'] * optimal_k
df['Cumulative_kx'] = (1 + df['Leveraged_Return']).cumprod()
# 4-3. 参考比較用に、たとえば2倍レバレッジの累積リターン
k_test = 2.0
df['Leveraged_Return_2x'] = df['Daily_Return'] * k_test
df['Cumulative_2x'] = (1 + df['Leveraged_Return_2x']).cumprod()
# ---------------------------
# 5. グラフで可視化
# ---------------------------
plt.figure(figsize=(10, 6))
plt.plot(df.index, df['Cumulative_1x'], label='No Leverage (1x)')
plt.plot(df.index, df['Cumulative_kx'], label=f'Optimal Leverage ({optimal_k:.2f}x)')
plt.plot(df.index, df['Cumulative_2x'], label='2x Leverage')
plt.title('S&P500 Index - Leverage Performance Comparison')
plt.xlabel('Date')
plt.ylabel('Cumulative Return')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
## 最適レバレッジ比率計算(μvsk)
import yfinance as yf
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import datetime
# ---------------------------
# 1. データの取得
# ---------------------------
start_date = "1990-01-01"
end_date = datetime.date.today().strftime("%Y-%m-%d")
df = yf.download('^GSPC', start=start_date, end=end_date)
df = df[['Adj Close']].dropna()
# 日次リターン
df['Daily_Return'] = df['Adj Close'].pct_change()
df.dropna(inplace=True)
# ここでは便宜上、サンプルとして「日次リターンが得られる行のみ」使う
returns = df['Daily_Return']
# ---------------------------
# 2. レバレッジ倍率ごとにリターンを計算
# ---------------------------
# 例えば 0倍(=現金保有)から5倍くらいまで 0.1 刻みで検証してみる
k_values = np.arange(0, 5.1, 0.1) # 0.0, 0.1, 0.2, ..., 5.0
# 結果を格納するリスト
annual_returns = [] # 年率リターン(幾何平均ベース)を格納
cagr_list = [] # CAGR(期間全体の累積リターン)を格納
for k in k_values:
# ---------------------------
# 2-1. 日次レバレッジリターン
# ---------------------------
# レバレッジを単純に掛けると「Daily_Return * k」
# 実務的にはコスト等あるが、ここでは単純モデル
leveraged_return = returns * k
# ---------------------------
# 2-2. 幾何平均リターン(年率換算)
# ---------------------------
# 幾何平均をとるには log(1+r) の平均を使う方法が一般的
# 日数ベースを年率に換算するには ≈ 252倍(米国株市場日数) などでスケーリング
log_ret = np.log1p(leveraged_return.dropna()) # log(1 + 日次レバレッジリターン)
mean_log_ret = log_ret.mean()
mean_log_ret_annual = mean_log_ret * 252 # 年率換算
# 年率リターン(幾何平均)
annual_return = np.expm1(mean_log_ret_annual) # exp(...) - 1
annual_returns.append(annual_return)
# ---------------------------
# 2-3. 期間全体の累積リターンから CAGR を計算
# ---------------------------
# (1 + r_t) を掛け合わせて、最終的に (最終価格/初期価格)^(1/年数) - 1 を求める方法
cumprod = (1 + leveraged_return).cumprod()
total_return = cumprod.iloc[-1] - 1.0 # 期間全体で何%のリターンか
n_days = len(leveraged_return.dropna())
n_years = n_days / 252.0 # 252営業日を1年と近似
# CAGR = (最終価値)^(1/年数) - 1
cagr = (1 + total_return) ** (1 / n_years) - 1
cagr_list.append(cagr)
# ---------------------------
# 3. グラフ描画
# ---------------------------
plt.figure(figsize=(12, 5))
# subplot(1,2,1) -- 幾何平均による年率リターン
plt.subplot(1, 2, 1)
plt.plot(k_values, annual_returns, marker='o')
plt.title('Annualized Return vs. Leverage (Geometric Mean)')
plt.xlabel('Leverage Ratio (k)')
plt.ylabel('Annualized Return')
plt.grid(True)
# subplot(1,2,2) -- 期間CAGR
plt.subplot(1, 2, 2)
plt.plot(k_values, cagr_list, marker='o', color='orange')
plt.title('CAGR vs. Leverage')
plt.xlabel('Leverage Ratio (k)')
plt.ylabel('CAGR')
plt.grid(True)
plt.tight_layout()
plt.show()