あらためてS＆P５００指数トレンドを確認する

2024年10月14日 08:39

サブテーマ：S＆P500の割高割安の判断と将来の変動幅を確認する

１　初めに

　今回は、表題の通り改めてS＆P500の長期トレンドを確認してみます。現在のS＆P500は最高値更新中のある意味絶好調な局面ではなるものの、これから投資する人にとっては割高に思えます。この割安割高感についてはバフェット指数やPERなどを引用し説明される専門家もおられますが結論はよくわからないと思われている方も多いと思います。
　今回シンプルにS＆P500を対数目盛としたうえでトレンド線を引いてみたらと思い解析してみた結果です。その結果、それなりのトレンドととして視覚化できましたのでみなさまの役に立つのではと考えました。私自身、自身の投資に対しても得るものが大きい結果でしたのでこの結果が少しでも役に立ったと思っていただければ幸いです。

今回のまとめ：
1950年から現在までのS＆P500の長期トレンド
　現在＋１σを超える位置で推移中＝やや割高
　ただし、過去＋１σのトレンド推移も長期にわたって続くこともある。
　　　　＋１σトレンドなら　2030年に　8000越え
　　　　　　　　　　　　　　2034年に　10000越え
　　　　ただし、-２σなら　2030年に　3440　の覚悟も必要
　＊中央線、±１σ、２σの２０４０年までの価格は本文中のテーブル参照

おまけ）GDPとインフレ率によるトレンド線の補正後（対数チャート）
＊この補正については検討の余地が大きいため、今後も検討続けてみます。具体的な成果があればこの場でご報告いたします。

今回からアウトプットを重視して、本文はPYTHONコードに触れず結果をご報告します。コード全文は最下部に全文公開しておきます。再現性を確保するため、GoogleColabを使って実行した結果としています。PYTHONを使ってみたい方勉強してみたい方はまずはコピペでぜひ触ってみてください。

２　豆知識

１）バフェット指数

　バフェット指数は、株式市場の割高・割安を判断するための指標です。株式市場の時価総額をその国のGDPで割って算出され、著名投資家ウォーレン・バフェット氏が重視しているとされています。一般的に、この指数が100%を超えると株価が割高、100%未満だと割安と判断されます。例えば、2023年7月時点の米国のバフェット指数は182%で、過去最高水準に達しており、株価が極めて割高な状態を示しています。ただし、この指数だけで投資判断を行うのは危険です。他の経済指標や市場動向、企業業績なども考慮する必要があり、またバフェット指数は国際比較や過去との比較が必ずしも正確にできないなどの限界もあります。

２）S&P500全体のPER推移

S&P500全体のPERは、米国株式市場全体の割安・割高を判断する上で重要な指標として紹介されています。

平均的な水準: S&P500の過去10年の平均PERは約18倍程度とされています

割安・割高の目安: 一般的に、PERが15倍以下で割安、20倍以上で割高と判断される傾向があります

現在の状況: 2024年4月時点でS&P500の予想PERは約21.7倍であり、やや割高な水準にあると考えられています

過去の変動: リーマンショック時には一時的にPERが123.73倍まで上昇するなど、極端な状況では通常の判断基準が適用できない場合もあります

他の指標との併用: PERだけでなく、経済状況、金利環境、企業の成長性なども考慮して総合的に判断することが重要です

業種による差: S&P500内でも業種によってPERの水準は大きく異なるため、個別の状況も考慮する必要があります

S&P500のPERは市場全体の評価を把握するための有用な指標ですが、これだけで投資判断を行うのではなく、他の要因も含めて総合的に分析することが重要です。

参考になったリンク：

３　実践

１）実施内容

　今回、第２次世界大戦終戦５年後からとして、１９５０年からの長期トレンドを確認することにしました。この１９５０年からの長期トレンドに対し、トレンドラインを確認するため対数グラフとして表示させたうえで、中央値と±１σ、２σの平行なトレンドラインを描きました。
　またこの中央値、±１σ、２σのトレンドラインが今後２０４０年までに具体的にどの値となるかをグラフとテーブルで出力しました。
　最後におまけとして、今の株価は割安か割高かをGDPとインフレ率に対して補正してみました。要はGDPが成長している時期はトレンドラインの傾きが＋、GDPが成長していない時期はトレンド－となる。またインフレ率は高いときは企業の業績もその分成長（＝株価UP）するためトレンドラインは＋、逆は－となると想定したものです。

２）長期トレンド（現在まで）

　初めにS＆P500の長期トレンドとその中央値、±１σ、２σの平行トレンドを描画すると下記の通りです。
過去から大まかにトレンドラインに沿ってS＆P500指数は上昇し続けていることがわかります。ほとんどは±２σの範囲ですが、プラスもマイナスもやや超えている時期があることもわかります。
その中で、現在のS＆P500指数は１σを超える水準ですが、１σの水準に到達してそれほど時期は経過しておらず、トレンドを眺めるだけでは今後もしばらくは+１σ+２σの推移をたどりそうにも見えます。

３）長期トレンド（将来）

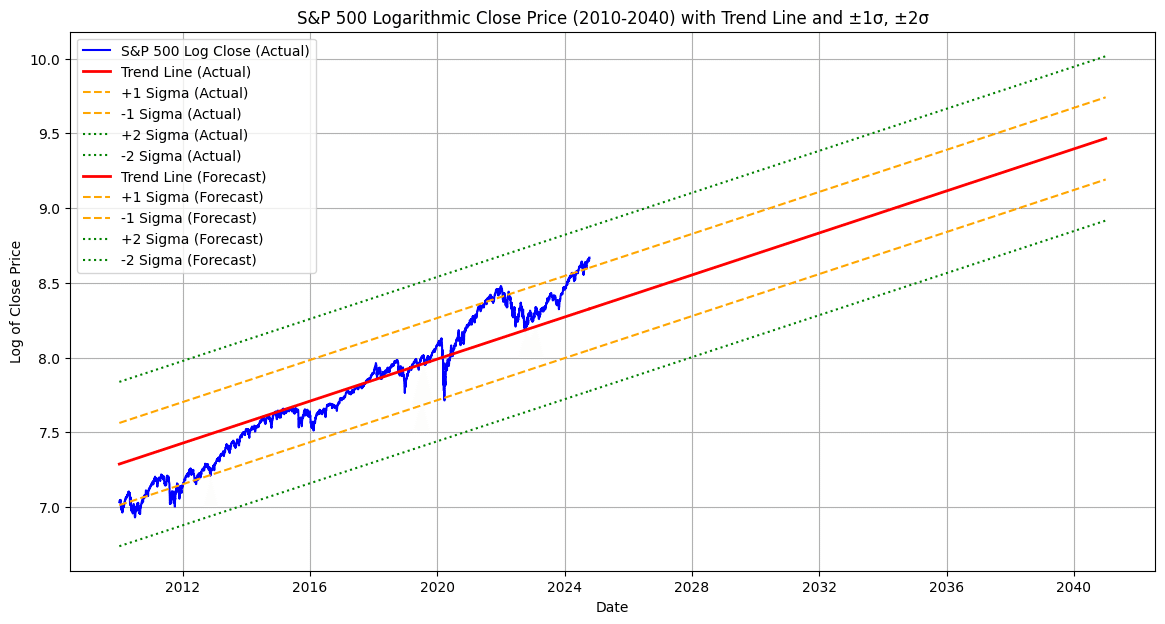
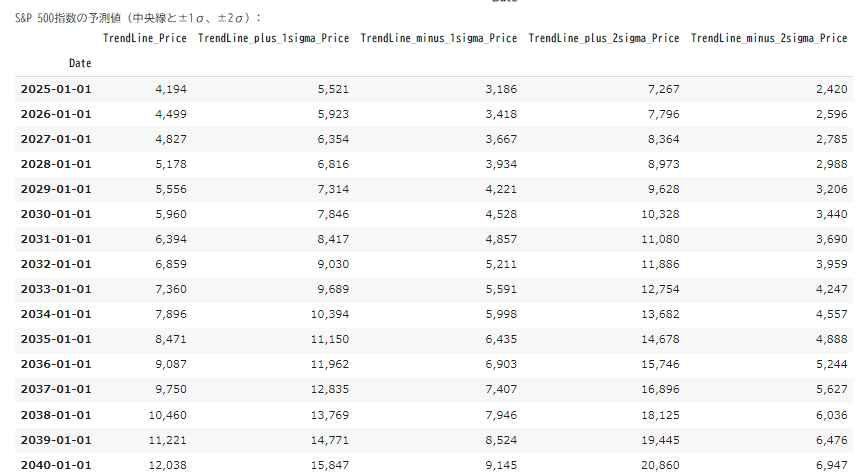
　次に、このトレンドラインが続くとどの水準かを可視化します。2010年から2040年までのトレンドを描くと下記のとおりです。またその具体的な各指数は下のテーブルを参照ください。
　その結果１σのトレンドに沿って上昇するとすると、2030年に8000越え、2034年に10000超え（今のほぼ倍）を達成する見込みです。
　逆に今から景気後退期に入ったり、その他株価暴落局面がくると-２σの水準までは覚悟しておく必要があると思います。今から約５年後２０３０年に-２σラインに到達するとすると、3440となり、今より30％程度は下がる余地があることもわかります。
　この上下の見込みを把握の上投資活動に皆様の投資活動の指標の１つになっていただければ幸いです。

４）おまけ　GDP、インフレ補正

　最後に、現在はGDPも成長しているし、インフレ率も高い時期を過ごしたため、＋1σオーバーの高い水準が妥当か再検証してみました。補正するとしてもその与える影響は１：１とも考えられずあくまで参考程度に確認いただければと思います。
　その結果は下記の通りで、中央値と１σの中央付近で割安ではないもののそれほど割高でない結果です。このままのアメリカ経済が成長するならこの水準もしくはその水準以上に成長する余地があると見ました。
皆様も改めてこの結果を眺めて感じて頂けるものがあれば幸いです。

S＆P500指数のGPD,インフレ補正後
＊この補正については検討の余地が大きいため、今後も検討続けてみます。具体的な成果があればこの場でご報告いたします。

４　最後に

　今回は投資の基本に戻ったS＆P500指数のトレンドについて深堀してみました。現在位置の把握、株価の上下の変動代が明確な数字として把握できたのではないでしょうか？
　FIRE等の目的達成のスケジューリング、自身の投資リスクの許容度について改めてお役立ていただければ幸いです。
　このサイトでは引き続き金融リテラシー向上及びＰＹＴＨＯＮプログラミングに関した情報を発信していきますので、ぜひ応援よろしくお願いします。
記事の感想、要望があれば下記X（旧Twitterまで）
＊今後の記事に活用させていただきます！！

Tweets by KotaKota978293

以下、過去記事、AI時系列予測等のご紹介
他サイトですがココならで、A I（LSTM）を使った株価予測の販売もやってます。こちらではFREDから、失業率や２年１０年金利、銅価格等結果も取得しLSTMモデルで予測するコードとなってますので興味があれば見てみてください。またその他２件も米国株投資とは直接関係はありませんがプログラム入門におすすめです。

チャンネル紹介：Kota＠Python＆米国株投資チャンネル

過去の掲載記事：興味PYがあればぜひ読んでください。
グラフ化集計の基礎：S &P500と金や米国債を比較してます。

移動平均を使った時系列予測

以下実行コード全文：コピペで実行してみてください。

import yfinance as yf
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import LinearRegression
from datetime import timedelta


# 1. データ取得と準備

# S&P 500データの取得（1950年から現在まで）
sp500 = yf.download('^GSPC', start='1950-01-01')

# 終値の対数を計算
sp500['LogClose'] = np.log(sp500['Close'])

# 日付データを数値に変換（経過日数）
sp500['DateNumeric'] = (sp500.index - sp500.index[0]).days

# 2. 線形回帰モデルの構築

# 説明変数（経過日数）の reshaping
X = sp500['DateNumeric'].values.reshape(-1, 1)
# 目的変数（対数終値）
y = sp500['LogClose'].values

# 線形回帰モデルの作成とフィッティング
model = LinearRegression()
model.fit(X, y)

# トレンドラインの予測値を計算
sp500['TrendLine'] = model.predict(X)

# 3. 残差とシグマの計算

# 残差の計算
sp500['Residuals'] = sp500['LogClose'] - sp500['TrendLine']

# 残差の標準偏差（シグマ）を計算
sigma = sp500['Residuals'].std()

# ±1シグマ、±2シグマの線を計算
sp500['TrendLine_plus_1sigma'] = sp500['TrendLine'] + sigma
sp500['TrendLine_minus_1sigma'] = sp500['TrendLine'] - sigma
sp500['TrendLine_plus_2sigma'] = sp500['TrendLine'] + 2 * sigma
sp500['TrendLine_minus_2sigma'] = sp500['TrendLine'] - 2 * sigma

# 4. グラフの作成

plt.figure(figsize=(14, 7))

# 対数終値のプロット
plt.plot(sp500.index, sp500['LogClose'], label='S&P 500 Log Close', color='blue')

# トレンドラインのプロット
plt.plot(sp500.index, sp500['TrendLine'], label='Trend Line', color='red', linewidth=2)

# ±1シグマの線のプロット
plt.plot(sp500.index, sp500['TrendLine_plus_1sigma'], label='+1 Sigma', color='orange', linestyle='dashed')
plt.plot(sp500.index, sp500['TrendLine_minus_1sigma'], label='-1 Sigma', color='orange', linestyle='dashed')

# ±2シグマの線のプロット
plt.plot(sp500.index, sp500['TrendLine_plus_2sigma'], label='+2 Sigma', color='green', linestyle='dotted')
plt.plot(sp500.index, sp500['TrendLine_minus_2sigma'], label='-2 Sigma', color='green', linestyle='dotted')

# グラフの装飾
plt.title('S&P 500 Logarithmic Close Price with Trend Line and ±1σ, ±2σ')
plt.xlabel('Date')
plt.ylabel('Log of Close Price')
plt.legend(loc='upper left')
plt.grid(True)
plt.show()

# ５. 予測期間の作成（現在から2040年まで）

# 予測期間の日付範囲を作成
future_dates = pd.date_range(start=sp500.index[-1] + timedelta(days=1), end='2040-12-31')

# 未来の日付データを数値に変換
future_date_numeric = (future_dates - sp500.index[0]).days.values.reshape(-1, 1)

# 未来のトレンドラインを予測
future_trend = model.predict(future_date_numeric)

# 未来の±シグマの線を計算
future_trend_plus_1sigma = future_trend + sigma
future_trend_minus_1sigma = future_trend - sigma
future_trend_plus_2sigma = future_trend + 2 * sigma
future_trend_minus_2sigma = future_trend - 2 * sigma

# 予測結果をデータフレームにまとめる
future_df = pd.DataFrame({
    'Date': future_dates,
    'TrendLine': future_trend,
    'TrendLine_plus_1sigma': future_trend_plus_1sigma,
    'TrendLine_minus_1sigma': future_trend_minus_1sigma,
    'TrendLine_plus_2sigma': future_trend_plus_2sigma,
    'TrendLine_minus_2sigma': future_trend_minus_2sigma
})

# 対数から元のスケールに戻す
future_df['TrendLine_Price'] = np.exp(future_df['TrendLine'])
future_df['TrendLine_plus_1sigma_Price'] = np.exp(future_df['TrendLine_plus_1sigma'])
future_df['TrendLine_minus_1sigma_Price'] = np.exp(future_df['TrendLine_minus_1sigma'])
future_df['TrendLine_plus_2sigma_Price'] = np.exp(future_df['TrendLine_plus_2sigma'])
future_df['TrendLine_minus_2sigma_Price'] = np.exp(future_df['TrendLine_minus_2sigma'])

# 5. 予測結果のテーブルを作成（年次データ）

# 各年の1月1日のデータを抽出
yearly_forecast = future_df[future_df['Date'].dt.strftime('%m-%d') == '01-01']

# 必要な列を選択
yearly_forecast = yearly_forecast[['Date', 'TrendLine_Price', 'TrendLine_plus_1sigma_Price',
                                   'TrendLine_minus_1sigma_Price', 'TrendLine_plus_2sigma_Price',
                                   'TrendLine_minus_2sigma_Price']]

# インデックスをDateに設定
yearly_forecast.set_index('Date', inplace=True)

# 6. テーブルの表示

# 数値列をフォーマットして文字列に変換
for col in ['TrendLine_Price', 'TrendLine_plus_1sigma_Price',
            'TrendLine_minus_1sigma_Price', 'TrendLine_plus_2sigma_Price',
            'TrendLine_minus_2sigma_Price']:
    yearly_forecast[col] = yearly_forecast[col].map('{:,.0f}'.format)
   
# 7. グラフの追加（2010年から2040年まで）

# 実績データの範囲を2010年以降に制限
sp500_recent = sp500[sp500.index >= '2010-01-01']

plt.figure(figsize=(14, 7))

# 実績データの対数終値をプロット
plt.plot(sp500_recent.index, sp500_recent['LogClose'], label='S&P 500 Log Close (Actual)', color='blue')

# 実績データのトレンドラインをプロット
plt.plot(sp500_recent.index, sp500_recent['TrendLine'], label='Trend Line (Actual)', color='red', linewidth=2)

# 実績データの±1シグマの線をプロット
plt.plot(sp500_recent.index, sp500_recent['TrendLine_plus_1sigma'], label='+1 Sigma (Actual)', color='orange', linestyle='dashed')
plt.plot(sp500_recent.index, sp500_recent['TrendLine_minus_1sigma'], label='-1 Sigma (Actual)', color='orange', linestyle='dashed')

# 実績データの±2シグマの線をプロット
plt.plot(sp500_recent.index, sp500_recent['TrendLine_plus_2sigma'], label='+2 Sigma (Actual)', color='green', linestyle='dotted')
plt.plot(sp500_recent.index, sp500_recent['TrendLine_minus_2sigma'], label='-2 Sigma (Actual)', color='green', linestyle='dotted')

# 未来予測のトレンドラインをプロット
plt.plot(future_df['Date'], future_df['TrendLine'], label='Trend Line (Forecast)', color='red', linewidth=2, linestyle='solid')

# 未来予測の±1シグマの線をプロット
plt.plot(future_df['Date'], future_df['TrendLine_plus_1sigma'], label='+1 Sigma (Forecast)', color='orange', linestyle='dashed')
plt.plot(future_df['Date'], future_df['TrendLine_minus_1sigma'], label='-1 Sigma (Forecast)', color='orange', linestyle='dashed')

# 未来予測の±2シグマの線をプロット
plt.plot(future_df['Date'], future_df['TrendLine_plus_2sigma'], label='+2 Sigma (Forecast)', color='green', linestyle='dotted')
plt.plot(future_df['Date'], future_df['TrendLine_minus_2sigma'], label='-2 Sigma (Forecast)', color='green', linestyle='dotted')

# グラフの装飾
plt.title('S&P 500 Logarithmic Close Price (2010-2040) with Trend Line and ±1σ, ±2σ')
plt.xlabel('Date')
plt.ylabel('Log of Close Price')
plt.legend(loc='upper left')
plt.grid(True)
plt.show()
   
# テーブルの表示
print("S&P 500指数の予測値（中央線と±1σ、±2σ）:")
yearly_forecast