
【量子力学】井戸型ポテンシャル
この記事では井戸型ポテンシャルにおける波動関数について考察する。
1. シュレディンガー方程式
シュレディンガー方程式は次のように与えられる。
$$
\begin{align*}
\bigg[ -\frac{\hbar^2}{2m}\frac{d^2}{dx^2} + V(x) \bigg]\psi(x) = E\psi(x)
~~~~~~~~~~~~~~~~~~~~\mathrm{(1)}
\end{align*}
$$
ここで、$${\psi(x)}$$は粒子の波動関数、$${V(x)}$$はポテンシャル、$${E}$$は粒子の持つ力学的エネルギーである。
この方程式は、ある粒子の状態とエネルギーが、その粒子の運動量($${\frac{p^2}{2m}}$$)とポテンシャルによって与えられる位置エネルギーによって決められていることを示している。これが三次元の場合、運動量は
$$
\begin{align*}
\mathbf{p}^2 &= p_x^2 + p_y^2 + p_z^2 \\
&= -\hbar^2\left( \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2}\right) \\
&= -\hbar^2 \nabla^2
\end{align*}
$$
のように表せるから、三次元のシュレディンガー方程式は
$$
\begin{align*}
\bigg[ -\frac{\hbar^2}{2m}\nabla^2 + V(\mathbf{x}) \bigg]\psi(\mathbf{x}) = E\psi(\mathbf{x})
~~~~~~~~~~~~~~~~~~~~\mathrm{(2)}
\end{align*}
$$
となる。しかし、簡単のため、この記事では一次元のシュレディンガー方程式について考えよう。
2. 井戸型ポテンシャルとは?
ある粒子を取り巻くポテンシャルにはさまざまな形が考えられるが、その中で最も初歩的なものが井戸型ポテンシャルである。
井戸型ポテンシャルでは、ある範囲内、例えば$${\Big[-\frac{a}{2}, +\frac{a}{2}\Big]}$$内でのポテンシャルが0で、それ以外では無限である。(Fig1を見よ)
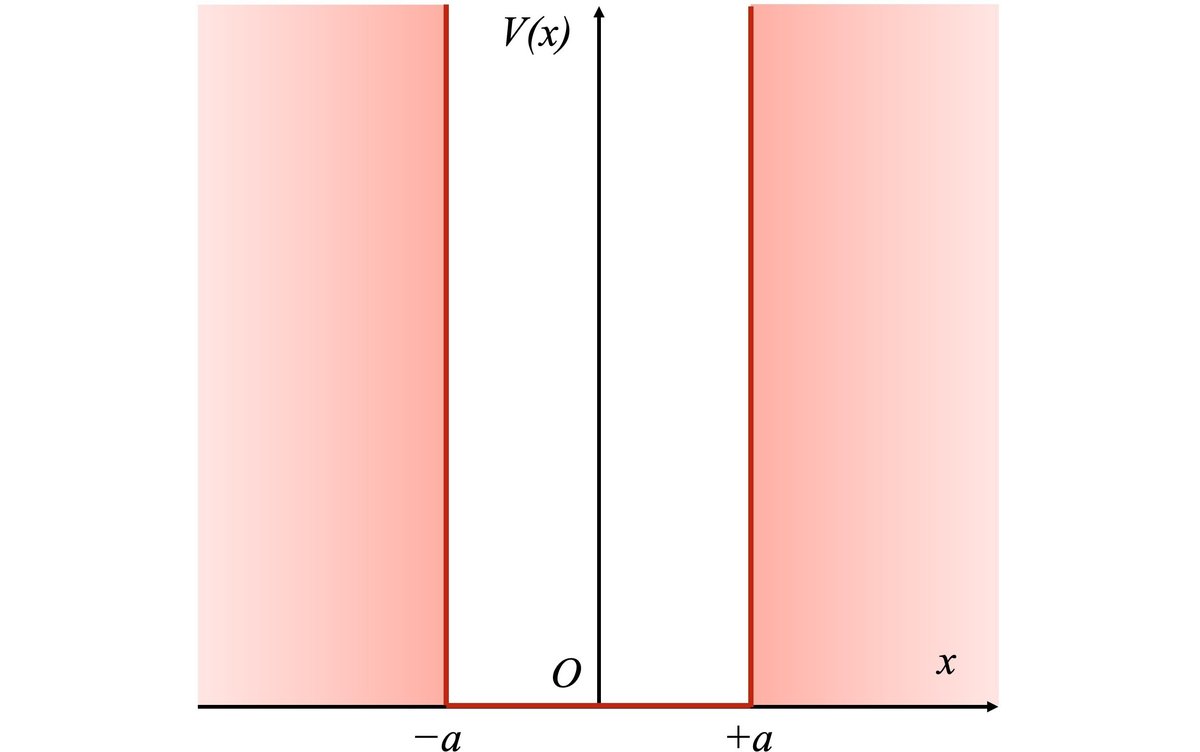
このポテンシャルは、一辺の長さが$${a}$$箱の中では粒子が何の拘束もなく自由に存在できるが、箱の外では存在しないような模型であると物理的に解釈することができる。(Fig2を見よ)

注意しなければならないのは、古典論的な描写とは異なり、粒子は箱の中で粒のように飛び回っているわけではないということだ。量子論的には、粒子の状態は波動関数$${\psi(x)}$$によって表現され、その波動関数によって箱の中での確率分布密度が決められる。
3. 波動関数の導出
3.1 一般解を求める
まずたちどころにわかることは、$${|x| < \frac{a}{2}}$$において$${\psi(x) = 0}$$ということである(そうなるように井戸型ポテンシャルは設定されている)。次に、$${|x| \leq \frac{a}{2}}$$ において、$${V(x) = 0}$$であるから、Eq.(2)は次のように書き直すことができる。
$$
\begin{align*}
-\frac{\hbar^2}{2m}\frac{d^2\psi(x)}{dx^2} &= E \psi (x)\\
\therefore~\frac{d^2\psi(x)}{dx^2} &= -\frac{2mE}{\hbar^2}\psi (x)~~~~~~~~~~~~~~~~~~~~\mathrm{(3)}
\end{align*}
$$
この最も初歩的な微分方程式の解は、一般的に次のようなものである。
$$
\begin{align*}
\psi(x) = A\cos\left( kx \right) + B\sin\left( kx\right) ~~~~~~~~~~ ~~~~~~~~~~\mathrm{(4)}
\end{align*}
$$
ここで、$${A, B \in \mathbb{R}}$$は振幅の定数で、$${k^2 = -\frac{2mE}{\hbar^2}}$$である。
3.2 境界条件
しかし、この解は境界条件を満たさなければならない。というのも、$${\psi(x)}$$は$${x = \pm\frac{a}{2}}$$にて井戸型ポテンシャルに課せられた条件、すなわち$${|x| < \frac{a}{2}}$$で$${\psi(x)}$$であることと連続的につながっていなければならない。
ただし、$${\psi(x)}$$の傾き、すなわち一階微分については、必ずしも連続的でなくても良い。このような条件を、ディリクレ境界条件(Dirichlet boundary condition, DBC)と呼称する。
さて、この条件を式に書き出すと、
$$
\begin{align*}
\psi\left(+\frac{a}{2} \right) = \psi\left(-\frac{a}{2} \right) = 0~~~~~~~~~~~~~~~~~~~~\mathrm{(5)}
\end{align*}
$$
これをEq.(4)に代入すると、
$$
\begin{align*}
\psi\left(+\frac{a}{2} \right) &= A\cos\left(+\frac{ka}{2} \right) + B \sin \left( +\frac{ka}{2} \right) \\
\psi\left(-\frac{a}{2} \right) &= A\cos\left(-\frac{ka}{2} \right) + B \sin \left( -\frac{ka}{2} \right) \\
&= A\cos\left(+\frac{ka}{2} \right) - B \sin \left( +\frac{ka}{2} \right)
\end{align*}
$$
$${\cos(\theta) + \sin(\theta) = 0}$$かつ$${\cos(\theta) - \sin(\theta) = 0}$$を同時に満たす実数$${\theta}$$は存在しないから、$${A = 0}$$か$${B = 0}$$かのいずれかひとつでなければならない。
まず、$${A=0}$$のとき、$${\cos}$$の項が消えるから、
$$
\sin\left(+\frac{ka}{2} \right) = 0 \Rightarrow k = \frac{2n\pi}{a} ~~~~(n = 0, 1, 2, …)
$$
次に、$${B = 0}$$のとき、$${\sin}$$の項が消えるから、
$$
\cos\left(+\frac{ka}{2} \right) = 0 \Rightarrow k = \frac{(2n+1)\pi}{a} ~~~~(n = 0, 1, 2, …)
$$
3.3 正規化
$${\psi(x)}$$に与えられるもう一つの条件として、正規化されていなければならないというものがある。すなわち、
$$
\int_{-\infty}^\infty dx~|\psi(x)|^2 = 1
$$
というのも、確率密度関数は波動関数を二乗することで得られ、確率の合計は必ず1になるためである。さて、このことを考慮すると、$${B = 0}$$のとき、
$$
\begin{align*}
\int_{-\infty}^\infty dx~|\psi(x)|^2 &= \int_{-\infty}^\infty dx ~ A_n^2~\cos^2\left(\frac{2n\pi}{a}x \right) \\
&= 2 A_n^2 \int_{0}^{+a/2}dx~~ \frac{1 +\cos \left (2\frac{ (2n+1)\pi}{a}x \right) }{2} \\
&= A_n^2 \bigg[ x + \frac{a}{2(2n+1)\pi}\sin\left (\frac{ 2(2n+1)\pi}{a}x \right) \bigg]_{x = 0}^{+a/2} \\
&= A_n^2\cdot \frac{a}{2} = 1 \\
\Rightarrow A_n &= \sqrt{\frac{2}{a}}~~~~~~~~~~~~~~~~~~~~\mathrm{(6)}
\end{align*}
$$
同様に$${A = 0}$$のときについても、$${B_n = \sqrt{\frac{2}{a}}}$$と求めることができる。まとめると、
$$
\begin{align*}
\psi_n(x) = \begin{cases} \sqrt{\frac{2}{a}} \cos\left(\frac{n\pi}{a}x
\right)~~~~~n = 1, 3, 5, …\\
\sqrt{\frac{2}{a}} \sin \left( \frac{n\pi}{a}x\right)~~~~~n = 2, 4, 6, …
\end{cases}~~~~~~~~~~~~~~~~~~~~\mathrm{(7)}
\end{align*}
$$
また、エネルギーも求めることができる。
$$
E_n = \frac{\hbar^2 k_n^2}{2m} = \frac{\hbar^2}{2m}\left( \frac{n\pi}{a}\right)^2~~~~~~~~~~~~~~~~~~~~\mathrm{(8)}
$$
$${n}$$が増えるごとに、エネルギーが二乗に比例して増えることが分かる。最後に、波動関数をプロットしてみると次のようになる。見やすさのため、$${x}$$軸のスケールは$${a}$$で割ってあり、$${y}$$軸のスケールは$${\sqrt{2/a}}$$で割ってある。

使用したpythonのコードは次の通り:
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Sat Dec 14 14:47:55 2024
@author: nampham
"""
import numpy as np
import matplotlib.pyplot as plt
def wave_function(n, a, x):
if n%2 == 0:
result = np.sqrt(2/a)*np.sin(n*np.pi*x/a)
else:
result = np.sqrt(2/a)*np.cos(n*np.pi*x/a)
result = np.where(abs(x) > a/2, 0, result)
return result
a = 2.00
x_list = np.arange(-1.50, 1.50, 0.01)
for n in range(1,5):
y_list = wave_function(n, a, x_list)
plt.plot(x_list, y_list, linewidth=0.8, label=f'n = {n}')
plt.title("Wave Function in Infinite Square Well (a = 2.0)")
plt.xlabel("x/a")
plt.ylabel("$\psi(x)$")
plt.xlim(-1.5, 1.5)
plt.ylim(-1.25, 1.25)
plt.vlines(1.0, -1.25, 1.25, color='black', linewidth=0.6)
plt.vlines(-1.0, -1.25, 1.25, color='black', linewidth=0.6)
plt.minorticks_on()
plt.grid()
plt.legend()
plt.show()
plt.close()3.4 直交性
これらの解は互いに直交している。というのも、$${\sin}$$と$${\cos}$$は正規直交基底(orthonormal basis)を作るからである。ほとんど自明なので証明はここで載せない。
$$
\int_0^{2\pi} d\phi~e^{i\phi_n}\cdot e^{i\phi_m} = 2\pi \delta_{nm}
$$
ゆえに、波動関数の一般解はこれらの解の線型結合で表せる。
$$
\psi(x) = \sum_{n = 1}^\infty c_n\psi_n(x) ~~~~~~~~~~~~~~~~~~~~\mathrm{(9)}
$$
4. 期待値
波動関数$${\psi_n(x)}$$における演算子$${\hat{O}}$$の期待値は
$$
\langle \hat{O} \rangle = \langle \psi_n(x) | \hat{O} | \psi_n(x) \rangle = \int_{-\infty}^\infty dx~\psi_n^*(x)\hat{O}\psi_n(x)
$$
で与えられる。ただし、$${\psi_n^*(x)}$$は複素共役(conplex conjugate)である。今回の場合、時間に依らない波動関数に複素数が出現しないので、単に二乗として以降の式で扱っているが、本来ならば複素共役に注意を払わねばならないことに留意してほしい。
4.1 位置の期待値
$$
\begin{align*}
\langle \hat{x} \rangle &= \frac{2}{a} \int_{-a/2}^{+a/2} dx~x~\sin^2 \left( \frac{n\pi}{a}x\right) \\
&= \frac{2}{a} \int_{-a/2}^{+a/2} dx~x~\frac{1 - \cos\left( \frac{2n\pi}{a}x\right)}{2}\\
\end{align*}
$$
$${\cos}$$の項が隅関数であるために、積分すると0になる。よって残る項は$${x/2}$$であり、
$$
\begin{align*}
\langle \hat{x} \rangle &= \frac{2}{a} \int_{-a/2}^{+a/2} dx~\frac{x}{2} = \frac{2}{a}\frac{x^2}{4}\bigg|_{-a/2}^{+a/2} = 0~~~~~~~~~~~~~~~~~~~~\mathrm{(10)}
\end{align*}
$$
結論として、$${n}$$に関わらず、$${x}$$の期待値は井戸の中心に位置する。
4.2 運動量の期待値
運動量の演算子は以下のとおりである。
$$
\hat{p} = -i\hbar \frac{d}{dx}
$$
よって、
$$
\begin{align*}
\langle \hat{p} \rangle &= \frac{2}{a} \int_{-a/2}^{+a/2} dx~\sin \left( \frac{n\pi}{a}x\right) \left( -i\hbar \frac{d}{dx} \right) \sin \left( \frac{n\pi}{a}x\right) \\
&= \frac{2}{a} \int_{-a/2}^{+a/2} dx~-i\frac{\pi\hbar n}{a} \sin \left( \frac{n\pi}{a}x\right) \cos \left( \frac{n\pi}{a}x\right) \\
&= -\frac{2i\pi\hbar n}{a^2}\int_{-a/2}^{+a/2} dx~\frac{1}{2}\sin \left( \frac{2n\pi}{a}x\right) \\
&= -\frac{i\pi\hbar n}{a^2} \Big[\frac{a}{2n\pi}\cos \left( \frac{2n\pi}{a}x\right) \Big]_{-a/2}^{+a/2} = 0 ~~~~~~~~~~~~~~~~~~~~\mathrm{(11)}
\end{align*}
$$
よって、全ての$${n}$$の場合について、運動量の期待値は0である。
4.3 ハミルトニアンの期待値
ハミルトニアンの期待値は、Eq.(8)で求められたエネルギーと等しいはずである。しかし、計算でも確かめてみよう。シュレーディンガー方程式より、$${|x| \leq \frac{a}{2}}$$において
$$
\hat{H}\psi(x) = \frac{p^2}{2m}\psi(x) = E\psi(x) ~~~~~~ ~~~~~~~~~~~~~~\mathrm{(12)}
$$
まず運動量の二乗の期待値$${\langle \hat{p}^2 \rangle}$$を求める必要がある。手順は、運動量の期待値を求めた時と同じである。ただし今回は
$$
\hat{p}^2 = \left( -i\hbar \frac{d}{dx} \right)^2 = -\hbar^2\frac{d^2}{dx^2}
$$
を代入する。
$$
\begin{align*}
\langle \hat{p}^2 \rangle &= \frac{2}{a} \int_{-a/2}^{+a/2} dx~\sin \left( \frac{n\pi}{a}x\right) \left( -\hbar^2\frac{d^2}{dx^2} \right) \sin \left( \frac{n\pi}{a}x\right) \\
&= \frac{2}{a} \int_{-a/2}^{+a/2} dx~\left(\frac{\pi\hbar n}{a}\right)^2 \sin \left( \frac{n\pi}{a}x\right) \sin \left( \frac{n\pi}{a}x\right) \\
&= \left(\frac{\pi\hbar n}{a}\right)^2 \cdot \frac{2}{a}\int_{-a/2}^{+a/2} dx~ \sin^2 \left( \frac{n\pi}{a}x\right) \\
&= \left(\frac{\pi\hbar n}{a}\right)^2 \int_{-a/2}^{+a/2} dx~\psi_n^2(x) \\
&= \left(\frac{\pi\hbar n}{a}\right)^2 = \hbar^2 k_n^2
\end{align*}
$$
これをEq.(12)に代入することで、
$$
\langle \hat{H} \rangle = \frac{\langle \hat{p}^2 \rangle}{2m} = \frac{\hbar^2 k_n^2}{2m}~~~~~~~~~~~~~~~~~~~~\mathrm{(13)}
$$
これは、Eq.(8)で求めたエネルギーの式に一致する!
参考文献
D. J. Griffiths and D. F. Schroeter, Introduction to Quantum Mechanics, 3rd ed. Cambridge: Cambridge University Press, 2018.
