
【中1数学】正負の数の乗法と除法
こんにちは、なぎさです。
今回は、正負の数の乗法と除法です。
乗法は掛け算、除法は割り算のこと。正の数と負の数が混じった掛け算、割り算のやり方と、「累乗」という新しい計算の表現について勉強していきます。
1. 掛け算のやり方
正の数、負の数の掛け算のやり方は、意外と簡単です。
①絶対値を掛け算する。
②符号をつける
これだけです。
①絶対値を掛け算するは、小学校でならった掛け算そのまま。
例えば、
2×(-3)の場合、絶対値は2と3なので、2×3=6
-5×(-8)の場合、絶対値は5と8なので、5×8=40
という普通の掛け算をやるということです。
次は、②符号をつける。
①で掛け算した結果に、「+」または「-」の符号をつけます。
ここが新しいところです。
正の数と負の数の掛け算では符号は「+」になるのか「ー」になるのか?
負の数同士の場合は「+」になるのか「-」になるのか?
どちらの符号がつくか、そのルールは「正負の数の加法と減法①」でやった符号の合体の仕方と同じです。
同じ符号の掛け算は「+」
「+」と「+」⇒「+」
「-」と「-」⇒「+」
違う符号の掛け算は「-」
「+」と「-」⇒「-」
「-」と「+」⇒「-」
それぞれの符号の組み合わせの計算例をみてみましょう。
「+」と「+」⇒「+」
+6×(+4)=+(6×4)=+24 (=24)
「-」と「-」⇒「+」
-9×(-2)=+(9×2)=+18 (=18)
「+」と「-」⇒「-」
+3×(-7)=-(3×7)=-21
「-」と「+」⇒「-」
-5×(+5)=-(5×5)=-25
どうでしょう。理解してもらえたでしょうか?
少し応用編として、3つの数字、4つの数字の掛け算の場合はどうなるか、やってみますね。

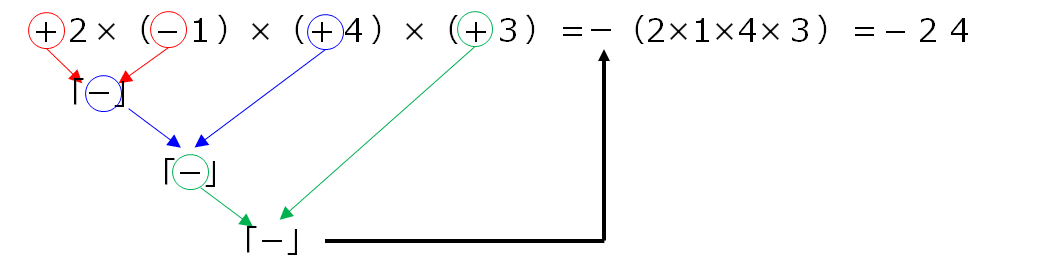
左から順に2つずつ組み合わせていけば、すべてを合体した符号が決まります。
2. 割り算のやり方
次に割り算のやり方ですが、
割り算は、逆数を掛けるのと同じこと
なので、最初に割り算を「逆数の掛け算」に置き換えてやれば、あとは先ほど学んだ掛け算のやり方と全く同じになります。
(割り算が逆数の掛け算になることは、分数のおさらい③で解説しています)
ということで、割り算の手順は
①割り算 ⇒ 逆数の掛け算に置き換える
②絶対値を掛け算する
③符号をつける。
となります。
一つ例を挙げてみましょう。

こんな感じです。
3. 累乗
同じ数字を繰り返し掛け算することを累乗といいまして、

のように表現し、「2の3乗」と読みます。
負の数や分数の累乗は、このようにカッコの外に指数を書いて表現します。

今度は、累乗をバラバラの掛け算に展開する場合で、いろいろなパターンを見てみましょう。
まずは間違いやすい例の一つ目。

上の式は、カッコの外に指数がある場合。この場合は、カッコの中全体を繰り返し掛け算するので、-3を4回掛けることになります。
それに対して、下の式は、-3にカッコがついていません。この場合は、3だけを繰り返し掛けて、最後に「-」の符号をつけることになります。
次もカッコの有無で計算が変わる間違いやすい例です。

上の式は、カッコの外に指数があるので、カッコの中にある分子と分母両方を繰り返し掛け算します。
それに対して、下の式は、カッコがついていません。この場合は、分子の2だけを繰り返し掛けることになります。
累乗の計算では、このようにカッコの付き方で計算が変わりますので、十分注意してください。
4. まとめ
ということで、今回は正負の数の掛け算と割り算、そして累乗について学んでみました。
割り算は逆数にすることで掛け算になる。これ、とても重要です。
今後は基本的に割り算は使わず、すべて逆数の掛け算、つまり分数の掛け算に変換して計算すると思ってください。(そのため、3回にもわたって分数のおさらいをやったのでした)
逆数にすることで、掛け算も割り算も計算のやり方は同じになります。
①割り算の場合 ⇒ 逆数の掛け算に置き換える
②絶対値を掛け算する
③符号をつける。
そして累乗。これは単なる同じ数の繰り返し掛け算なのですが、具体例で示したように、カッコの付き方で計算が変わるということだけ、十分注意してくださいね。
次回は、加減乗除、つまり足し算、引き算、掛け算、割り算が混じった計算(これを四則計算といいます)について勉強していきたいと思います。
