
Art of Kernel Trick
最高に美しい数学テクニックである、カーネル法について説明する。
線形分離不可能問題
問題設定
次のような1次元1入力の線形判別式を考える。
$$
y = w x + b
$$
$${(x,y)}$$は次のようになっていると考える。$${y}$$は$${-1}$$か$${1}$$をとり、$${-1}$$は青、$${1}$$が赤であるとする。

どう見ても線形分離不可能だがこういう問題は良くある。例えば「あなたが平熱であるかどうか調べる」とか。
特徴空間
高次写像
適当な関数で変換して2次元の入力にしてみる。
$$
\phi_1(x) = x
$$
$$
\phi_2(x) = x^2
$$
$$
y = w_1 \phi_1(x) + w_2 \phi_2(x) + w_0
$$
2乗してるだけだ。これだと線形分離できそうに見える。

このように低次元上の非線形分離を高次元上の線形分離に置き換えると良いことがある。この高次元の空間を機械学習では特徴空間(feature space)という。
多様体
ところで、$${(\phi_1,\phi_2)}$$の取りうる値の範囲には明らかに次の性質がある。
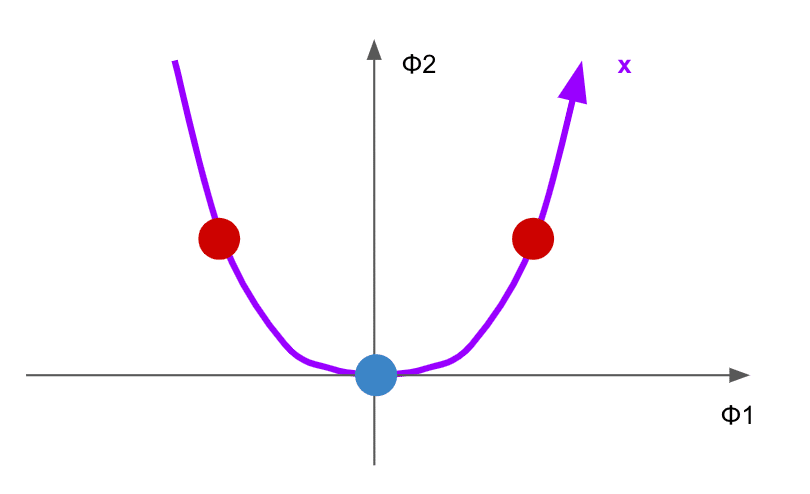
$${x}$$という曲線上($${\phi_1^2 = \phi_2}$$)の値しか取らない。こういうのを多様体(manifold)という。これは素朴に考えると当たり前で、元々が1次元の情報しかもっていないのだから、その情報を2次元に拡張しても本質的には1次元分の情報しかない。
逆に考えてみよう。これはある高次のデータがあったときに、そのデータが多様体上に分布しているならば、適当な低次元のデータに変換できることを示唆する。これを埋め込み(embedding)という。ここでは詳しく扱わないが、機械学習ではone-hot vectorな特徴量の次元を「小さくする」のに使える。
線形判別
実際に判別式を求めてみる。これは線形回帰、つまり一般化逆行列の問題として解ける。
3つの点に対して
$$
\mathbf{\Phi} = \begin{bmatrix} \phi_1(x^{(1)}) && \phi_2(x^{(1)}) && 1 \\ \phi_1(x^{(2)}) && \phi_2(x^{(2)}) && 1 \\ \phi_1(x^{(3)}) && \phi_2(x^{(3)}) && 1 \\ \end{bmatrix} = \begin{bmatrix} 1 && 1 && 1 \\ -1 && 1 && 1 \\ 0 && 0 && 1 \\ \end{bmatrix}
$$
$$
\mathbf{Y} = \begin{bmatrix} y^{(1)} \\ y^{(2)} \\ y^{(3)} \\ \end{bmatrix} = \begin{bmatrix} 1 \\ 1 \\ -1 \\ \end{bmatrix}
$$
これに対して次を解けば良い。
$$
\mathbf{W} = (\mathbf{\Phi}^T \mathbf{\Phi})^{-1}\mathbf{\Phi}^T \mathbf{Y}
$$
今回の場合は3次元だから普通の逆行列で解ける。
$$
\mathbf{W} = \mathbf{\Phi}^{-1} \mathbf{Y} = \begin{bmatrix} 0.5 && -0.5 && 0 \\ 0.5 && 0.5 && -1 \\ 0 && 0 && 1 \\ \end{bmatrix} \begin{bmatrix} 1 \\ 1 \\ -1 \\ \end{bmatrix} = \begin{bmatrix} 0 \\ 2 \\ -1 \\ \end{bmatrix}
$$
よって
$$
y = 2 \phi_2(x) -1
$$
これを借りた。
$${x}$$の関数で書くと
$$
y = 2 x^2 - 1
$$
検算してみる。1のとき1、0のとき-1、-1のとき1。あってる。このように元の空間で線形分離できなくても、高次の空間では線形分離できることがある。
内積とカーネル法
ここで特徴空間上のデータセット$${\mathbf{\Phi}}$$の特異値分解を考えてみる。
$$
\mathbf{\Phi} = \mathbf{U} \mathbf{\Sigma} \mathbf{V}^T
$$
行ベクトルが1つのサンプルを表すから、そのグラム行列は
$$
\mathbf{\Phi} \mathbf{\Phi}^T = \mathbf{U} \mathbf{\Sigma}^2 \mathbf{U}^T
$$
その成分は
$$
\mathbf{\Phi} \mathbf{\Phi}^T = [\mathbf{\phi}(x^{(i)})^T \mathbf{\phi}(x^{(j)})]
$$
この内積計算している部分を適当なカーネル関数で置き換える。
$$
\mathbf{K} = [\mathbf{\phi}(x^{(i)})^T \mathbf{\phi}(x^{(j)})] = [k(x^{(i)},x^{(j)})]
$$
これをカーネル法(あるいはカーネルトリック)という。
元のベクトルを高次の特徴空間に写像する
特徴空間空間上で内積を計算する
これをまとめて
カーネル関数を計算する
これで済ませる。こうすると高次の特徴空間を直接計算しなくても良くなる(ことがある)。しかもこれなら、内積を計算できさえすれば良いわけだから特徴空間はベクトル空間でなくても良い。
例えばラベルが未知の適当な$${x'}$$からなる$${\mathbf{\Phi}'}$$があったすると、これに対する予測値は
$$
\mathbf{Y}' =\mathbf{\Phi}' \mathbf{W} = \mathbf{\Phi}' (\mathbf{\Phi}^T \mathbf{\Phi})^{-1}\mathbf{\Phi}^T \mathbf{Y}
$$
これを実際に計算可能な$${\mathbf{\Phi} \mathbf{\Phi}^T}$$と$${\mathbf{\Phi}' \mathbf{\Phi}^T}$$で置き換えることができれば、$${\phi_m(x)}$$を明示的に計算できなくても変換を求められる。
ちなみに、さっきの2次元の特徴空間だと具体的な値は
$$
k(x^{(i)},x^{(j)}) = \mathbf{\phi}(x^{(i)})^T \mathbf{\phi}(x^{(j)}) = x^{(i)} x^{(j)} + (x^{(i)} x^{(j)})^2 + 1
$$
普通の内積を線形カーネルというが、上の式は線形カーネルを少しだけ拡張している。より一般的には多項式カーネルと言って
$$
k(x^{(i)},x^{(j)}) = (x^{(i)} x^{(j)} + c)^d
$$
こういう形をとる(1次元で計算しているので内積はただの掛け算になっていることに注意してほしい)。さっきの計算は2次の多項式カーネルを使っている場合と同値である。元の次元よりも大きい適当な$${d}$$次の多項式カーネルを使えば、カーネル計算だけで高次の特徴空間上で計算することと同じ結果が得られる。
カーネル主成分分析
主成分分析(principal component analysis)をカーネル法で解いてみる。データ数を$${n}$$とすると共分散行列は
$$
\mathbf{C} = \frac{1}{n} \mathbf{\Phi}^T \mathbf{\Phi}
$$
高次写像は明示的に計算できない場合を考えると、上の式は実際には計算できないことに注意したい。固有値分解を考える。
$$
\mathbf{C} = \frac{1}{n} \mathbf{V} \mathbf{\Sigma}^2 \mathbf{V}^T
$$
このとき主成分分析による変換は
$$
\mathbf{Y} = \mathbf{\Phi} \mathbf{V}
$$
これを共分散行列ではなくグラム行列で解けば良い。グラム行列(カーネル行列)を考えると
$$
\mathbf{K} = \mathbf{\Phi} \mathbf{\Phi}^T = \mathbf{U} \mathbf{\Sigma}^2 \mathbf{U}^T
$$
これは計算できる($${ \mathbf{\Phi}}$$、$${ \mathbf{C}}$$、$${ \mathbf{V}}$$は計算できない。$${ \mathbf{K}}$$、$${ \mathbf{U}}$$、$${ \mathbf{\Sigma}}$$は計算できる)。よって
$$
\mathbf{Y} = \mathbf{\Phi} \mathbf{V} = \mathbf{U} \mathbf{\Sigma}
$$
実際には特徴空間上で平均をゼロにする必要がある(これもカーネル関数で計算できる)。
データを高次元の特徴空間に写像する
特徴空間上で主成分分析(共分散行列の固有値分解)して次元削減する
これを
カーネル行列を計算する
カーネル行列を固有値分解する
で済ませてしまっている。
RBFカーネル
カーネルについては、RBFカーネル(ガウシアンカーネル)だけ紹介しておく。
$$
k(x^{(i)},x^{(j)}) = \exp (- \gamma \| x^{(i)} - x^{(j)} \|^2)
$$
$${x^{(i)}}$$と$${x^{(j)}}$$が等しい時に最大値の1、離れれば離れるほどゼロに近づく。カーネル行列を計算するとは、すべてのデータに対してこれを計算することだから、これは結果的に最近傍法(nearest neighbor algorithm)と同じ効果をもたらす。
Support Vector Machine
クラス分類法の一種、SVMについても紹介しておく。詳しくは説明しないがSVMの特徴は
線形分離の一種であり、その解法は二次計画問題に帰着する
カーネル法を適用できる
分離境界を表現するのにSV(support vector)を使うが、これが疎(sparse)になる
つまり
数学的には確実に解けて、汎用の計算パッケージが使えて
非線形分離ができて
その解を最小の特徴で表現
できる。さっきのカーネル主成分分析にRBFカーネルを使うと、中身としては最近傍法と同じだから元の全データセットを使う必要があるが、SVMだと分離境界周辺の有限個のSVだけあれば良い。しかも数学的な保証つき。これはすごい。SVMが一時期流行ったのは数学的に美しいからだと思う。
再生核ヒルベルト空間
さっきこう言った。
内積を計算できさえすれば良いわけだから特徴空間はベクトル空間でなくても良い。
カーネル法を使える特徴空間を再生核ヒルベルト空間(reproducing kernel Hilbert space)という。
要するに
ヒルベルト空間:ベクトル空間(内積空間)をもっと抽象的にしたもの
核:カーネル関数を使う
再生:特徴空間に写して、元に戻す
特徴空間がベクトル空間の場合は
$$
\phi(x) = {\displaystyle \sum_{i=1}^n} \alpha_i k(x, x^{(i)})
$$
カーネル計算の線形結合で表現できる写像となる。最初の3点を高次元に移したとき、こういう形が成立するかやってみよう。
$$
k(x,x^{(i)}) = x x^{(i)} + x^2 (x^{(i)})^2 + 1
$$
これを
$$
\phi_1(x) = {\displaystyle \sum_{i=1}^3} \alpha_i k(x, x^{(i)})
$$
$$
\phi_2(x) = {\displaystyle \sum_{i=1}^3} \beta_i k(x, x^{(i)})
$$
に入れて、$${x^{(1)}=1}$$、$${x^{(2)}=-1}$$、$${x^{(3)}=0}$$を代入して整理すると
$$
\phi_1(x) = (\alpha_1 - \alpha_2) x + (\alpha_1 + \alpha_2) x^2 + (\alpha_1 + \alpha_2 + \alpha_3)
$$
$$
\phi_2(x) = (\beta_1 - \beta_2) x + (\beta_1 + \beta_2) x^2 + (\beta_1 + \beta_2 + \beta_3)
$$
$${\alpha_1=\frac{1}{2}}$$、$${\alpha_2=-\frac{1}{2}}$$、$${\alpha_3=0}$$、$${\beta_1=\frac{1}{2}}$$、$${\beta_2=\frac{1}{2}}$$、$${\beta_3=-1}$$とすると、$${\phi_1(x) = x}$$と$${\phi_2(x) = x^2}$$となる。ちゃんと成立した。
こう考えるとRBFカーネルの利用結果が最近傍法っぽくなる理由がわかる。
$$
\phi(x) = {\displaystyle \sum_{i=1}^n} \alpha_i \exp (- \gamma \| x - x^{(i)} \|^2)
$$
これは実質的に(正規分布を利用した)確率を表す関数の形になっている。こういう風にカーネルをつかって確率密度関数を表現することをカーネル密度推定という。
おわりに
まとめると
観測できる空間から観測できない高次空間に写像する
高次空間で何らかの(簡単な)処理を行い、観測できる空間に返す
結果的に観測できない空間の処理を容易に行うから、これをtrickと称する。
ユークリッド距離は
$$
\| \mathbf{x} - \mathbf{y} \|^2 = \mathbf{x}^T\mathbf{x} - 2 \mathbf{x}^T\mathbf{y} + \mathbf{y}^T\mathbf{y}
$$
このように内積表現だけで計算できる。つまり、
$$
\| \mathbf{\phi(x)} - \mathbf{\phi(y)} \|^2 = k(\mathbf{x},\mathbf{x}) - 2 k(\mathbf{x},\mathbf{y}) + k(\mathbf{y},\mathbf{y})
$$
高次空間上における距離はカーネル関数を通して低次元の表現だけで計算できる。これはすごい。
また、逆に思考実験してみよう。我々が観測できる次元における複雑な現象は、観測できない高次元上の単純な法則に従っているのかもしれない。
参考、数学と物理のシリーズ
この記事が参加している募集
この記事が気に入ったらサポートをしてみませんか?
