
虚数が何の役に立つのか
梅雨でも元気に数学ぞい。
今日は虚数(imaginary number)の話題。中学3年生くらいに理解されることを目指す。かなりうろ覚えのまま書くので間違っていたら指摘してほしい。
解のない方程式
まず、次の方程式の解は実数(real number)ではない。
$$
x^2 = -1
$$
こんな数ないだろ。ないのでこれを虚数(imaginary number)という。
こんなものが何の役に立つのか。これを考える前に数の歴史を振り返ろう。
数の歴史
物を数える
「りんごが1つ、みかんが2つ」
数(number)とは、数える(count)ことだ。これは小学1年生の知識である。この数は足し算を定義できる。
「りんごが2つ、りんごが3つ、足したらいくつ?」
$$
2 + 3 = 5
$$
さらにこの数は引き算を定義できる。
「りんごが5つ、3つを食べたらいくつになる?」
$$
5 - 3 = 2
$$
さて、実はこの数には計算できない計算が存在する。次のようなものだ。
「りんごが3つ、5つを食べたらいくつになる?」
$$
3 - 5 = ???
$$
りんごを扱う上でこれは計算不可能であり、解なしである。だが、全くできないとは思わない。多くの人は$${-2}$$と答えるかもしれない。これは直感的に次を意味する。
符号は足りないことを表す
数字はどれくらい足りないかを表す
これが存在しないが役に立つ数だ。今日において、これは負の数(negative number)と呼ばれるが、驚くなかれ、このような数は大昔には虚数と呼ばれた。存在しないからだ。存在しないからそう呼んでいた。
量を測る
歴史を進める。物を数えるだけだと不便であることに気づく。
「5つのりんごを2人で食べる」
1個を余らせても良いが少しもったいないので1つを分割した方が良さそうだ。これが分数(fraction)である。小数(decimal)は「分母が10の分数の簡略表現」だから同じ意味を持つ。
さて、この時点で数とは数えるものではなく、量(volume)である。これでコップの中の水量を測ることができる。
分数は整数(integer)によって表現できる。だからこの世界のすべての数は整数で表現できる、かに思われた。
無理数
2辺の長さが1の直角二等辺三角形の斜辺の長さは、ピタゴラスの定理によって次の方程式の解であるが、この解は分数で表現できない。
$$
x^2 = 2
$$
これを無理数(irrational number)という。一方、2個の整数の分数で表現できるものを有理数(rational number)という。
$$
\frac{b}{a}
$$
有理数と無理数を使うとこの世界の量の全てを表現することができる。
実数
ゼロ(zero)について説明する。ゼロの発見とは、ゼロがあることの発見ではなく、ゼロを計算に使うと便利なことを発見したという意味だ。
$$
5 + 0 = 5
$$
そもそもこれがないと、負の数(negative numer)を表現できない。0より小さい数を負の数、0より大きい数を正の数(positive number)という。これらを合わせて実数(real number)という。
今おかしなことを言った。「0より小さい」とは何だ?これは日本語として成立していないのではないか。そのとおり。正しくは「0より低い数を負の数、0より高い数を正の数」と呼ぶべきだ。
なぜこう呼ぶべきなのか。それは負の数という概念が入ると、数は量ではなく位置(position)として扱われるからだ。
北に3mの位置を3、南に5mの位置を-5
セルシウス温度で0より20高ければ20℃、0より10低ければ-10℃
実数とは数直線上の位置である。符号が方向(direction)、絶対値が原点との距離(distance to origin)を表す。
負の数と負の数を掛け算すると正の数になるのはなぜか?符号は方向だから、正の数の掛け算は方向をそのままに、負の数の掛け算は方向を反転させるという解釈ができる。
複素数
最初の方程式に戻る。
$$
x^2 = -1
$$
この解を$${x = i = \sqrt{-1}}$$とおいてみよう。これを虚数単位(imaginary unit)というが、明らかに次の性質を持つ($${i}$$をひたすらかける)。
$$
i^2 = -1
$$
$$
i^3 = -i
$$
$$
i^4 = 1
$$
$$
i^5 = i
$$
$$
i^6 =i^2 = -1
$$
ループしている。同じことが何度も周期的に繰り返される。これは重要な性質で後で虚数がなぜ役に立つかのヒントになる。
さてそれはそれとして、存在しないとしても役に立つことはある。最初の方で、負の数は存在しないが役に立つと言ったが、あれは正の数直線上に存在しないという意味で、実数の数直線上には存在した。
では虚数は?結論としては、実数直線(1次元直線)には存在しないが、実数軸に虚数軸を加えた複素数平面(2次元平面)には存在する。さっき、実数は位置(position)であると言った。実数とは1次元空間上の点の位置で、複素数は2次元空間上の点の位置を表す。
$$
a + b i
$$
これを複素数(complex number)という。ここで$${a}$$と$${b}$$は実数であり、$${b = 0}$$である複素数を実数、そうでない複素数を虚数という。言い換えると、2次元平面上で実数軸上に存在する点を実数、それ以外を虚数という。

これただの2次元の変数では?そのとおり、複素数は2次元ベクトルと等価である。両方とも線形代数であるという言い方が適切かもしれないが、大学1年生の数学が必要になるのでここでは端折る。
虚数の空間
乗算の解釈
さきほど、負の数の掛け算は方向を反転させると書いた。これは2回繰り返すと同じ位置に戻るからだ。-1をかけることは位置を180°回転させることを意味する。
では、虚数の掛け算は何が起きているだろうか。4回繰り返すと同じ位置に戻っている。虚数単位iをかけることは位置を90°回転させることを意味する。
もっと正確に言うと、複素数同士の掛け算は点の回転を表現できる。ベクトル的に言うと次の通り
足し算:平行移動
掛け算:回転、および、拡大縮小
引き算:足し算の逆
割り算:掛け算の逆
回転(rotation)の何が便利かというと、周期的(cyclic)な計算と極めて相性が良い。
回転運動と周期関数
少し、数学ではなく物理の話をする。
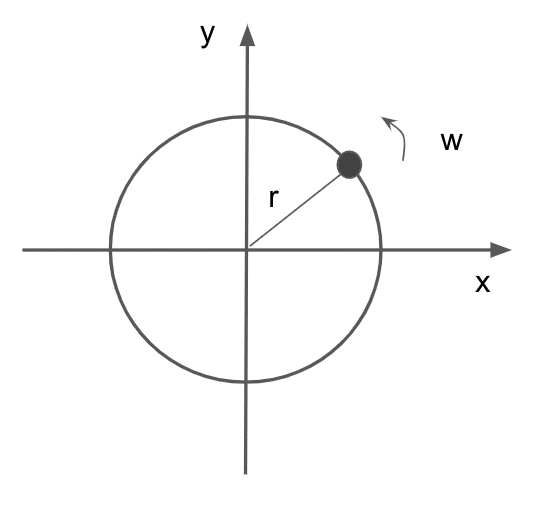
半径$${r=A}$$の円上を角速度$${w}$$で等速円運動しているとする。初期の角度($${x}$$軸に対する角度)を$${\phi}$$として、時刻を$${t}$$とするとその座標は
$$
x = A \cos(w t + \phi)
$$
$$
y = A \sin(w t + \phi)
$$
となる。

要するに三角関数(triangular function)である。左図の半径、角速度、初期角度が、右図ではそれぞれ振幅(amplitude)、角周波数(angular frequency)、位相(phase)に相当する。
これを$${\theta}$$だけ回転させることを考える。三角関数の中身に$${\theta}$$を足せばよいだけでは?そのとおり。だが、複素数を使うとこれを極めてエレガントに表現できる。さっき、虚数の掛け算は回転だと書いた、逆に回転は掛け算の形で書くことができる。
$$
z = x + y i
$$
これに対して
$$
\cos(\theta) + i \sin(\theta)
$$
を乗じると$${(x,y)}$$を原点を軸に$${\theta}$$だけ回転させたものになる。これはすごい。
$$
(x + y i)(\cos(\theta) + i \sin(\theta)) = x \cos(\theta) - y \sin(\theta) + i (x \sin(\theta) + y \cos(\theta))
$$
これは明らかに行列演算の形でかける。
$$
\begin{bmatrix} \cos(\theta) && -\sin(\theta) \\ \sin(\theta) && \cos(\theta) \\ \end{bmatrix}\begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x \cos(\theta) - y \sin(\theta) \\ x \sin(\theta) + y \cos(\theta) \end{bmatrix}
$$
ベクトルに直交行列を乗じることは、幾何的にはベクトルの回転だからこれは完全に理にかなっている。
掛け算を足し算のように扱うことができる関数がある。指数関数(exponential function)だ。
$$
a^b a^c = a^{b + c}
$$
掛け算をすると足し算になる、これはなにかに似ている。角度だ。複素数同士を掛け算すると、その角度は足し算になる。これを簡潔に書いたのが次の式だ。
$$
e^{i \theta} = \cos(\theta) + i \sin(\theta)
$$
これをオイラーの公式という。
級数展開とフーリエ級数
さらに難しい数学をしてしまうが、ある関数を別の関数の線形和で表現することを級数展開という。何を言っているのかわからないのと思うので特に有名なものを紹介する。1つ目はテイラー展開の特別な場合であるマクローリン展開。
$$
f(x)= {\displaystyle \sum_{n = 0}^{\infty}} \frac{f^{(n)}(0)}{n!} x^n
$$
要するに、適当な多項式の組み合わせで任意の関数を再現することができる。2つ目はフーリエ変換の特別な場合であるフーリエ級数。任意の周期関数に対して、次のように展開できる。
$$
f(x)= {\displaystyle \sum_{n = 0}^{\infty} a_n \sin(n x + \phi_n)}
$$
これは任意の周期関数は適当な正弦波の重ね合わせで表現できることを意味する。複素数を使って良いなら簡単にかける。
$$
{\displaystyle \sum_{n = 0}^{\infty} c_n e^{i (n x + \phi_n)}}
$$
これだけだと何の役に立つのかわかりにくいが、足したり引いたりする時にとても役に立つ(物理学の世界で波の重ね合わせといわれるやつだ)。
さらに、進んだり遅れたりした信号を足したり引いたりするときにはもっと役に立つ(例えば、振幅と位相の異なる三角波を100個足し算する計算をしてみてほしい、私だったら絶対にやりたくないがフーリエ変換を使っていいならこれは難しくない)。
おわりに
段々何が言いたいのかわからなくなってきたため、というかどう見ても中学生に理解できない記事になってしまったため、このあたりで締める。
存在しないが役に立つ数を虚数という
虚数は回転や周期的なものを計算するのにとても役に立つ
この世界のほとんどの現象は周期的なものの組み合わせで表現できる
このあたりを覚えておいてほしい。
