
numpyと、アダマール積
はじめに
皆さん、こんにちは。
今回は、アダマール積と、numpy 上でのアダマール積の実現方法について、話をさせていただこうと思います。
numpyとは!?
numpy は、プログラミング言語 python における特定の計算を、高速に実施するためのライブラリになります。
先ず、python については、別途以下の記事もありますので、よかったら参照下さい。
numpy に関しては、以下の記事が numpy の高速化について触れていますので、こちらもよかったら参照下さい。
アダマール積とは!?
アダマール積については、wikiに詳しい説明がありました。
一言で説明すれば、wiki中にある以下の画像のような形になります。

要するには、同じ要素数を持った行列、或いは、ベクトルについて、同座標同士の掛け合わせを行う計算の仕方になります。
対して、一般的な行列積は、異なる計算仕様になります。
行列積や線形代数の基本的な考え方については、以下の記事を参照いただけたらと思います。
アダマール積の計算仕様をイメージにすると、以下の様になります。
尚、アダマール積の記号は、○になります。


同座標の値同士を掛け合わせて、その掛け算の結果を、同座標にセットする形です。
一方、行列積の計算仕様は、以下イメージとなります。


numpyで実装すると、どうなるか?
上記の例を、numpy で実装すると、以下のようになります。
import numpy as np
A = np.array([[1, 4],
[3, 6],
[8, 2]])
B = np.array([[3, 2],
[5, 1],
[7, 10]])
print('A * B = ')
print(A * B)
print()
print('A.T @ B = ')
print(A.T @ B)出力結果は以下になります
A * B =
[[ 3 8]
[15 6]
[56 20]]
A.T @ B =
[[74 85]
[56 34]]
特殊なケースにおける、numpyのアダマール積的な計算仕様
アダマール積は、基本的に要素数が等しい行列同士、ベクトル同士での計算が基本ではありますが、実際には、もう少し拡張したい時があったりします。
例えば、行列とベクトルとをアダマール積的に計算するケースです。
ケースとしては、ベクトルが縦であるケースと、横であるケースとの2つがあります。
前者ケースのイメージは以下です。
numpy でアダマール積と同様に
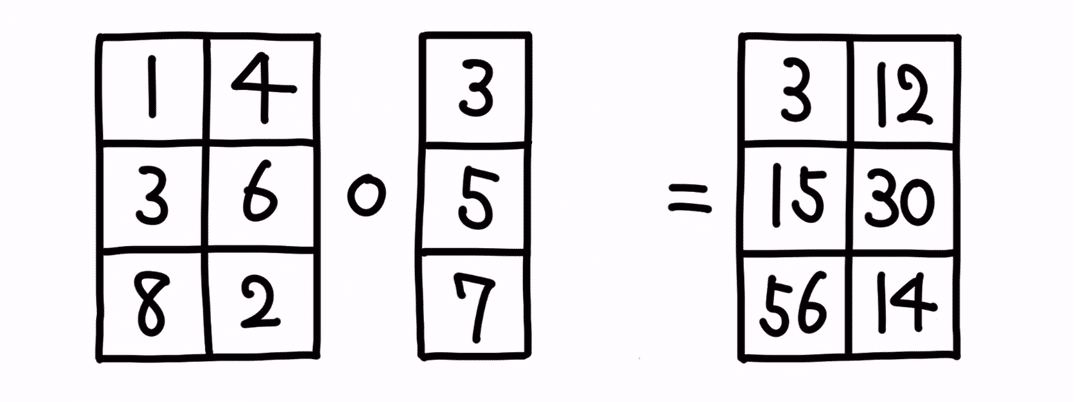
これは、要するには、縦のベクトルを、横にコピーして、アダマール積を取るような形です。

後者ケースのイメージは以下です。
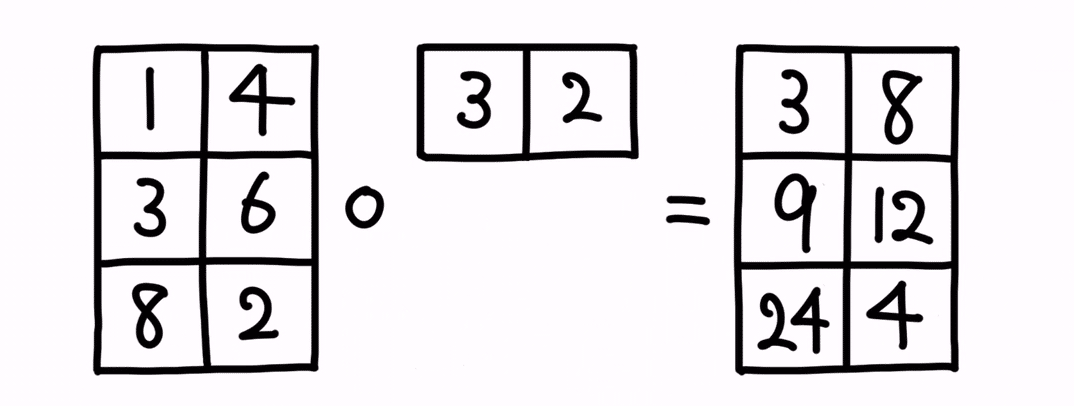
こちらも、横のベクトルを、縦にコピーして、アダマール積を実施してくれます。

或いは、行列とスカラーの掛け算の場合は、行列の全要素に対して、定数倍を実施する形になります。

こちらも、要するには、スカラーを縦横にコピーしてから、アダマール積を実施している形です。

尚、アダマール積、或いは、アダマール積的な計算をする場合、掛け算記号の前後の変数が入れ替わっても、計算結果は変わりません。
import numpy as np
A = np.array([[1, 4],
[3, 6],
[8, 2]])
b = np.array([[3],
[5],
[7]])
c = np.array([[3, 2]])
d = np.array([3])
print('A * b = ')
print(A * b)
print()
print('b * A = ')
print(b * A)
print()
print('A * c = ')
print(A * c)
print()
print('c * A = ')
print(c * A)
print()
print('A * d = ')
print(A * d)
print()
print('d * A = ')
print(d * A)プログラムの出力結果は以下となります。
A * b =
[[ 3 12]
[15 30]
[56 14]]
b * A =
[[ 3 12]
[15 30]
[56 14]]
A * c =
[[ 3 8]
[ 9 12]
[24 4]]
c * A =
[[ 3 8]
[ 9 12]
[24 4]]
A * d =
[[ 3 12]
[ 9 18]
[24 6]]
d * A =
[[ 3 12]
[ 9 18]
[24 6]]
一方、行列積の場合は、例えば、行列 A と行列 B について、AB と BA の結果は異なります。
A = np.array([[3, 2],
[1, 6]])
B = np.array([[4, 3],
[2, 1]])
print('A @ B = ')
print(A @ B)
print()
print('B @ A = ')
print(B @ A)プログラムの出力結果は、以下となります。
A @ B =
[[16 11]
[16 9]]
B @ A =
[[15 26]
[ 7 10]]
解釈がややこしいので、いっそfor文にしてしまえば…
上記、アダマール積的な計算に関しては、解釈が若干難しいので、なんならfor文を使って計算を表現した方が良いのではないか…?と思えてくる方もいることでしょう。
しかし、実は、python には、for 文によるパフォーマンス低下の問題があります。
numpy の機能を用いて、for 文を使わずに実装した方が、最適化されたライブラリ機能をフルに使うことで、パフォーマンスが格段に向上するのです。
その辺りについては、以下の記事にまとめられていますので、参考にして下さい。
記事中に実施した実験では、1000万個の要素を持つ行列同士のアダマール積にて、250倍程の高速化が実現されています。
250倍の高速化というと…。
高速化のスケールとして、「4分 → 1秒」、「4時間 → 1分」、「10日 → 1時間」という具合です。
スゴい違いですね。
その為、仕様を理解して、numpy を使ったアダマール積演算を行うことには、とても意味があります。
おわりに
以上で、アダマール積に関する記事を終えます。
ここまで読んでくださった方、本当にありがとうございました。🙇
