
機械学習と綿密な学問、線形代数について
はじめに
皆さん、こんにちは。
今回は、機械学習と切っても切れない密接な関係にある、線形代数という学問について、書かせていただきたいと思います。
機械学習とは?
機械学習については、別途以下の記事に書いていますので、良かったら参照下さい。
線形代数とは?
線形代数とは、大学で習う、ちょっと高度な数学のジャンルになります。
大学数学です。
線形代数の大目的を、誤解を恐れず、簡潔に言ってしまえば、「複雑な計算を簡潔に表現すること」です。
共通化・一般化された概念でくるんであげて、計算の複雑性を緩和するのです。
汚い部屋だと新しい発想や前向きな考えが生まれづらいように、数学における思考整理の役割として、大いに役立ってくれるものが線形代数となります。
特に、機械学習という技術分野は、分析対象とするデータが多数存在し、計算が複雑化しやすい為、理論をデータ量に依らず一般化させることは、非常に重要です。
線形代数は、大いにその助けとなる形です。
一度、仲良くなったら、もう線形代数無しには、機械学習と向き合いたくなくなる程にです。
尚、細かい説明については、以下の記事の説明が分かりやすいので、参考にしていただけたらと思います。
さて、私の方では、誤解を恐れずに、もう少し砕けた説明を試みようと思います。
先ず、大まかな特徴としては以下があります。
【線形代数の特徴】
(1)高校数学までには無かった、数字の集まりという概念が存在する
(2)高校数学で勉強したΣ記号(足し算の繰返しを表す記号)を、式から省略することができる
(3)その他、特殊な性質や計算仕様が存在する
以上。
線形代数の特徴:(1)数字の集まりという概念
線形代数の特徴について、先ず、「(1)高校数学までには無かった、数字の集まりという概念が存在する」という点について掘り下げます。
中学や高校の数学にて、例えば、連立方程式などで、式の中に文字が存在する形は見たことがあるかと思います。
「2x + 3y = 8」などです。
この式について、中学や高校の数学ですと、この文字に含まれる値は、ある単一の数字だったかと思います。
上の式で言えば、「x = 1, y = 2」などです。
線形代数においては、この概念が少し拡張されます。
数式中の文字については、単一数字の意味合いだけでなく、複数数字の集まりという意味が導入されるのです。
尚、単一数字と複数数字の概念は、以下の3つに整理されます。
[1]スカラー : 1 ✕ 1 の単一数字
[2]ベクトル : N ✕ 1 の複数数字
[3]行列 : N ✕ D の複数数字
以上。
1つずつ説明します。
[1]のスカラーについてですが、これは、中学・高校で扱ってきたような、1つの文字が1つの数字を持つ概念です。
言葉の意味を調べてみると、「大きさのみで表され、方向を持たない量」と出てきます。
つまりは、単一の数字ということです。
敢えて、複数数字を持つ概念に合わせて表記をすると、スカラーは「1 ✕ 1」というサイズの複数数字概念という形になります。
イメージは以下です。
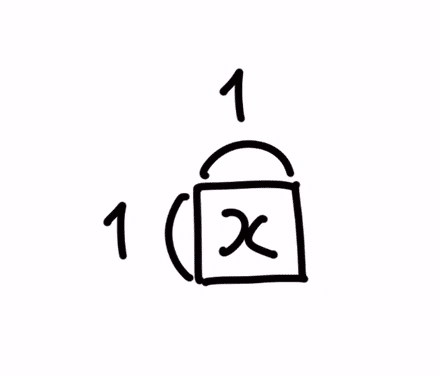
尚、スカラーは、線形代数の式表現では、細字の小文字で表現することが多いです。
[2]のベクトルですが、これは、数字を一列に並べた概念となります。
言葉の意味を調べてみても、「要素を(縦または横に)一列に並べたもの」と出てきます。
プログラミング経験者の方向けに説明するならば、「1次元の配列」というと分かりやすいかもしれません。
イメージは以下です。

尚、ベクトルは、線形代数の式表現では、太字の小文字で表現することが多いです。
そして、各要素を表現する際は、x𝚒 という形で表現します。
[3]の行列ですが、これは、数字を縦横に長方形状・正方形状に並べた概念となります。
言葉の意味を調べると、「数字・文字を長方形や正方形に並べたもの」と出てきます。
英語では、マトリックスといいます。
こちらは、プログラミングでいうところの「2次元の配列」になります。
イメージは以下です。

尚、行列は、線形代数の式表現では、太字の大文字で表記されることが多いです。
各要素を表現する際は、x𝚒𝚓 という形で表現します。
以上、紹介した3つの概念が、線形代数では用いられます。
先ずは、こういう概念があるということを覚えてもらえたらと思います。
線形代数の特徴:(2)Σ記号の省略
線形代数の特徴について、次に、「(2)高校数学で勉強したΣ記号(足し算の繰返しを表す記号)を、式から省略することができる」という点について掘り下げます。
線形代数は、スカラーとベクトルと行列とを、それぞれ掛け合わせることができます。
掛け合わせる組合せ毎に、計算の仕方が異なりますので、1つずつ説明していきます。
掛け合わせ計算の組合せとしては、以下が有り得ます。
〔1〕スカラー ✕ スカラー
〔2〕ベクトル ✕ スカラー
〔3〕スカラー ✕ ベクトル
〔4〕ベクトル ✕ ベクトル
〔5〕行列 ✕ ベクトル
〔6〕ベクトル ✕ 行列
〔7〕行列 ✕ 行列
以上。
1つずつ説明していきます。
計算の仕方〔1〕 : スカラー ✕ スカラー
先ずは、「〔1〕スカラー ✕ スカラー」の計算の仕方です。
これは、通常の数字と数字の掛け算となります。
イメージとしては、以下となります。

数字をセットすると、以下の感じです。

これは、算数や、中学・高校の数学における計算と同様ですね。
尚、線形代数の掛け算にはルールがあります。
それは、✕記号の左にある変数の横の要素数と、✕記号の右にある変数の縦の要素数とが、等しくないと掛け合わせができない、というルールです。
スカラー同士の掛け算であれば、必ず掛け合わせができます。
なぜならば、お互いに縦横の要素数が「1 ✕ 1」だからです。
その整合性を捉えるのに、分かりやすい確認の仕方が以下です。
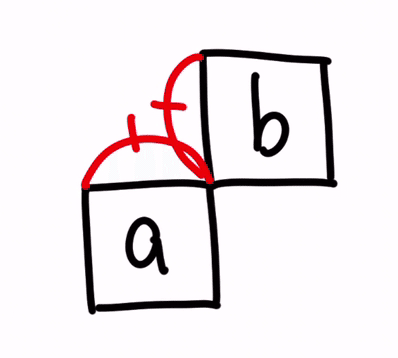
a ✕ b を計算する場合、a の横の要素数と、b の縦の要素数が同じでないと、掛け算ができませんが、それがイラストの赤部分になります。
赤部分の長さが等しくないと、掛け算ができないという訳です。
一目瞭然で分かりやすいですね。
(※この計算の仕方は、私が師匠から教えていただいた、とても貴重な概念となります。横展開の許可をいただきました。出典は、岩波書店から何れかの書籍にあった情報とのことです。)
また、更にもう一点、この表現の嬉しさとして、出力の行列サイズが一目瞭然であることが挙げられます。
実は、a と b とでできた隙間が、出力の変数のサイズになるのです。
イメージは以下です。
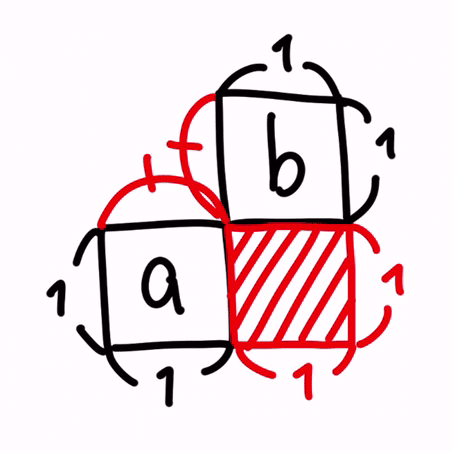
つまり、✕記号の左にある変数の縦の要素数と、✕記号の右にある変数の横の要素数とが、出力の縦横要素数となる訳です。
まとめると、上記のように、式中における、✕記号の左右にある変数を、左下と右上に並べることで、以下が一目瞭然という訳です。
- 掛け合わせができるかどうかが、簡単に判定できる
- 式中における、✕記号の左にある変数の横の要素数と、✕記号の右にある変数の縦の要素数とが、等しくないと掛け合わせができない
- 出力の変数の縦横要素数が、簡単に求められる
- 式中における、✕記号の左にある変数の縦の要素数と、✕記号の右にある変数の横の要素数とが、出力の縦横要素数となる
この確認方法は、線形代数全般に適用できるので、以降の説明でも使っていきます。
計算の仕方〔2〕 : ベクトル ✕ スカラー
次に、「〔2〕ベクトル ✕ スカラー」の計算の仕方です。
a がベクトルで、b がスカラーだとして、a ✕ b の計算のイメージは、以下となります。

先ず、掛け合わせの条件は問題無しです。
a の横の要素数と、b の縦の要素数が、共に1である為、計算が可能です。
また、a の縦の要素数が3、b の横の要素数が1である為、出力変数の要素数は、縦3 ✕ 横1のベクトルとなります。
そして、出力変数の各要素がどうなるかというと、以下のイメージです。

左側にある要素 a𝚒 から横に伸ばした線と、右側にある要素 b から縦に伸ばした線とが、交差するポイントにて、a𝚒 ✕ b の掛け算をします。
これが、出力変数の各要素の値になります。
仮に、数値を入れて確認してみると、以下です。
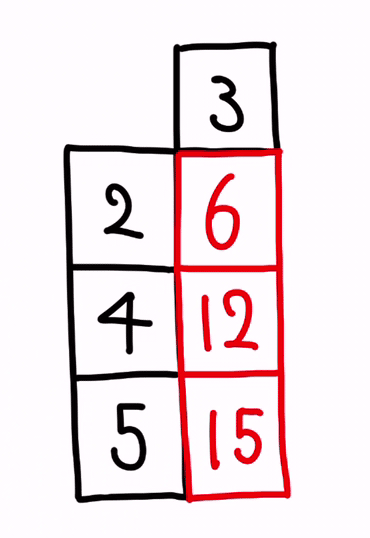
以上が、ベクトルとスカラーとを掛け算する方法になります。
計算の仕方〔3〕 : スカラー ✕ ベクトル
次に、「〔3〕スカラー ✕ ベクトル」の計算の仕方です。
a がスカラーで、b がベクトルだとして、a ✕ b の計算のイメージは、以下となります… が…

…という感じで、計算ができません。
左側変数の横要素数と、右側変数の縦要素数が、合っていない為です。
この問題を解決するには、転置という計算操作を行います。
転置とは、ベクトルや行列において、縦と横の要素を入れ替えることです。
ベクトルの転置は、縦長のものが横長になるように、90°倒します。
尚、ベクトルは、一般的に縦長と定義されることが多いです。
その為、転置されたベクトルが横長となることが一般的です。
(※たまに、転置前が横長、転置後が縦長として記載されているドキュメントも存在します。)
転置を表す式記号は、変数文字の右上に T を置くこととなります。
よって、b は縦長の数字配列となり、bᵀ は横長の数字配列となります。
尚、b の一番上に配置されていた要素は、bᵀ だと一番左に配置され、b の一番下に配置されていた要素は、bᵀ だと一番右に配置されます。
イメージは以下です。

その為、スカラー ✕ ベクトルは掛けるためには、ベクトルを転置してあげれば計算できます。
つまり、a ✕ bᵀ という式ならば、計算ができるということになります。
イメージは以下です。

計算結果を、文字で表すと、以下となります。

仮に数値を入れてみると、以下のようになります。
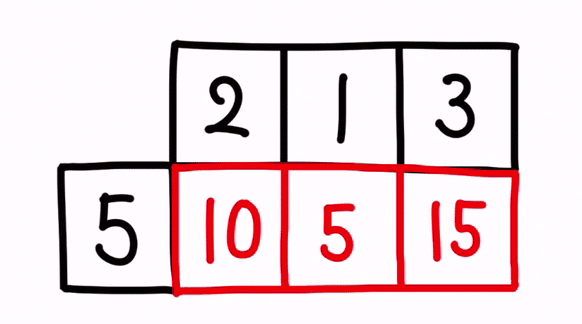
以上が、スカラーとベクトルとを掛け算する方法になります。
計算の仕方〔4〕 : ベクトル ✕ ベクトル
次に、「〔4〕ベクトル ✕ ベクトル」の計算の仕方です。
a がベクトルで、b がベクトルだとして、a ✕ b の計算をする上では、先程紹介した転置を用いる必要があります。
以下のイメージで、掛け算ができない為です。

尚、転置を用いる場合には、2通りのパターンがあります。
1つは、掛け算の左側の変数を転置するパターンで、式にすると aᵀ ✕ b です。
或いは、✕記号を省略して、aᵀb です。
一般に、✕記号は、省略することができます。
もう1つは、掛け算の右側の変数を転置するパターンで、式にすると a ✕ bᵀ です。
✕記号を省略すると、abᵀ です。
この2パターンの計算イメージは、以下となります。

この2パターンは、要素数が合っているために計算ができます。

それでは、それぞれについて、どう計算がされるかを説明していきます。
aᵀb については、以下のような計算手順になります。
先ず、添字の番号が同じ者同士を掛け算します。

そして、それらの合計を算出します。
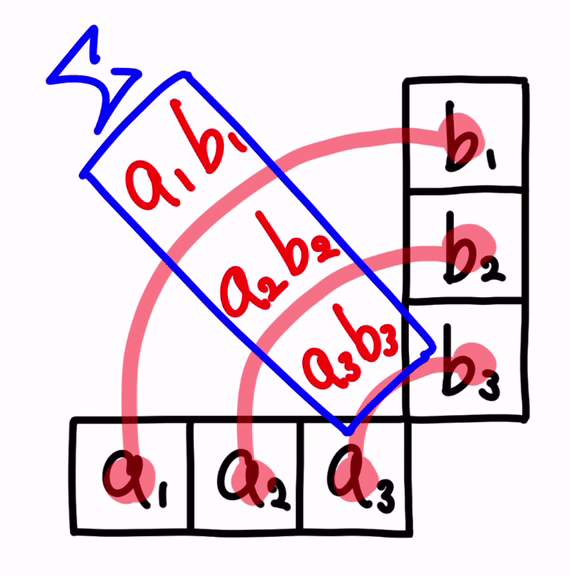
合計値は、a₁b₁ + a₂b₂ + a₃b₃ となり、それがベクトルが交差する先にセットされます。

以上が、aᵀb のパターンにおける、ベクトルとベクトルとを掛け算する方法になります。
尚、途中の図に、Σ という記号が登場しました。
これは、「合計」や「総和」という意味の数学記号となります。
最もオーソドックスな Σ の使い方は、以下です。

Σ 記号は、足し算を繰り返すというオペレーションを示しています。
i は、添字と呼ばれるインデックスで、ベクトルの要素番地のようなものです。
Σ 記号の下側にある「i = 1」にて、繰り返しの際に使う添字が i であり、それを1からカウントアップしていく、という意図が表現されています。
そして、Σ 記号の上側にある 3 は、添字のカウントアップの終了値となっています。
その為、上記ですと、i は {1, 2, 3} とカウントアップされていく形になります。

よって、aᵀb = a₁b₁ + a₂b₂ + a₃b₃ = Σ a𝚒b𝚒 (𝚒=1〜3) という形です。
仮に、ベクトルに値を入れてみると、以下の結果となります。

掛け算と足し算の繰り返しですね。
尚、掛け算のことは「積(せき)」、足し算のことは「和(わ)」と表現したりします。
そして、上記のような、掛け算と足し算の繰り返しのことを、積和演算といったりします。
機械学習には、この積和演算が、頻出します。
さて、ベクトルとベクトルの掛け算のもう一方、abᵀ についてですが、そちらは以下のようなイメージとなります。

縦横の組合せで、交差する位置で掛け算をするような形です。
基本的な考え方は、ベクトルとスカラーを掛ける場合と似ています。
尚、aᵀb の時のような、足し算は登場しません。
それは、上記における a の横の要素数と、bᵀ の縦の要素数が1である為です。
aᵀb の場合は、それらが2以上でした。
そうなってくると、足し算が登場し始めます。
まあ、この辺りは、線形代数における計算のルールですので、深く考えず、覚えてしまえば良いポイントとなります。
計算の仕方〔5〕 : 行列 ✕ ベクトル
次に、「〔5〕行列 ✕ ベクトル」の計算の仕方です。
A が行列で、b がベクトルだとして、A ✕ b の計算をするイメージは以下となります。

さて、ここからはパズルになります。
この場合の計算は、ベクトルとベクトルとの掛け算の繰り返しになります。
先ず、A の行列の一番上の行と、b のベクトルとを、掛け算します。

次に、A の行列の2番目の行と、b のベクトルとを、掛け算します。

後は、同じ要領で、3行目・4行目・5行目と繰り返して行きます。

そうすると、出力の変数が算出されます。
尚、出力の変数は、ベクトルとなります。
ベクトル b の横の要素数が1である為です。

仮に、値を入れてみると、以下となります。
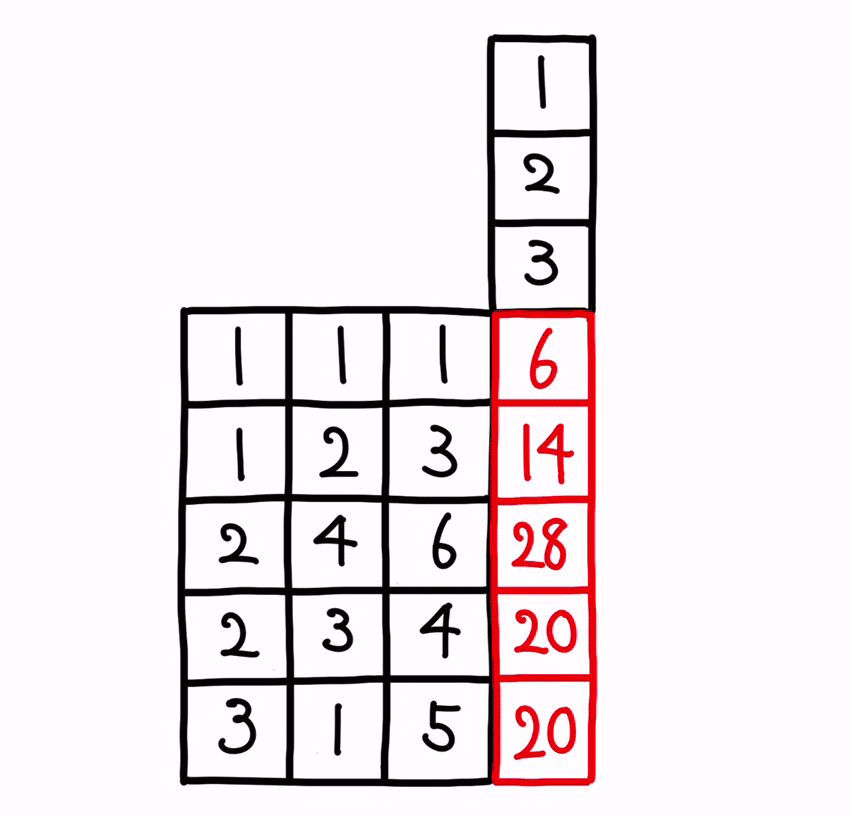
以上が、行列とベクトルとの掛け算の方法となります。
計算の仕方〔6〕 : ベクトル ✕ 行列
次に、「〔6〕ベクトル ✕ 行列」の計算の仕方です。
a がベクトルで、B が行列だとして、a ✕ B の計算をするイメージは以下となります。

ベクトル a は、転置しないと掛け算ができないので、転置します。
そして、積和演算は、以下のイメージの様に行います。
先ずは、ベクトル a と、行列 B の一番左の列とを、ベクトルとベクトルとの積和演算のように計算します。

同じ要領で、行列 B の2列目・3列目についても、積和演算を実施します。

そうすることで、出力変数の各要素が算出されます。
尚、出力の変数は、ベクトルとなります。

仮に、値を入れてみると、以下の様になります。

以上が、ベクトルと行列との、掛け算の方法となります。
計算の仕方〔7〕 : 行列 ✕ 行列
最後に、「〔7〕行列 ✕ 行列」の計算の仕方です。
A も B も行列だとして、A ✕ B の計算イメージは以下となります。

計算手順は、これまでの応用となります。
✕記号の左側変数の行ラインと、✕記号の右側変数の列ラインとが、交差するポイントの計算結果が、それぞれのライン上に乗っているベクトルとベクトルとの掛け算の結果となる形です。

出力変数は、行列となります。
その行列1つ1つの要素を眺めますと、以下のイメージです。

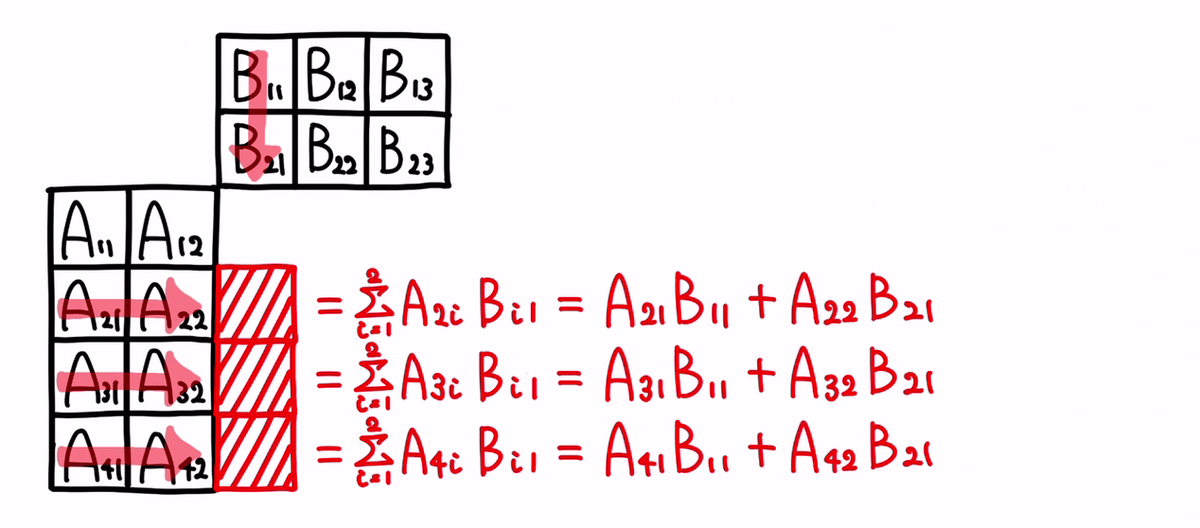


以上。
行列をベクトル毎に切り取って、その掛け算をしちゃえば良い感じですね。
線形代数の特徴:(3)特殊な性質や計算仕様
線形代数の特徴について、最後に、「(3)その他、特殊な性質や計算仕様が存在する」という点について掘り下げます。
ここまでの説明でも、ベクトル・行列の掛け算や、転置といった、線形代数特有の考え方を紹介してきましたが、それ以外にも特有の考え方が存在します。
特有の計算方法ともいえるでしょう。
その中で、特に紹介する必要があるのは、単位行列と逆行列の2つです。
それらを押さえれば、線形代数を用いた考え方の大枠が捉えられた、といって過言ではないかと思います。
恐縮ながら、誤解を恐れずに、そう表現させていただこうと思います。
実際には、他の学問同様、知れば知るほど掘り下げられる形で、どんどん深い学問議論が広がっていくのですが、先ずは単位行列と逆行列の2つを知れば、入り口としての視界はクリアになります。
さて、先ず、単位行列についてですが、これはベクトルや行列に単位行列を掛けると、出力として、元のベクトルや行列が、そのまま計算されるものです。
具体的には、縦の要素数と、横の要素数とが等しい正方行列で、かつ対角成分のみが 1、残る成分が 0 で構成されるものです。
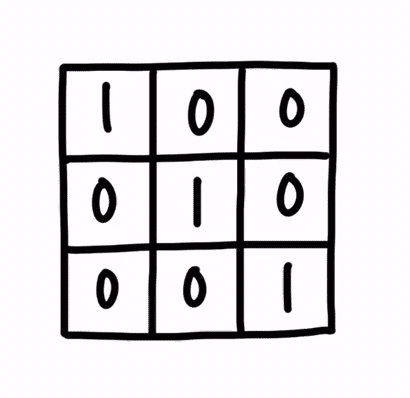
この行列は、I という文字で表されることが一般的です。
アルファベットの I(アイ)です。
スカラーの 1 に、あるスカラーを掛けると、計算結果は、掛けたあるスカラーがそのまま出力されますよね。
「1 ✕ 3 = 3」という具合に。
単位行列の場合も、例えば、ベクトル a については、「I ✕ a = a」となります。
行列 B については、「I ✕ B = B」となります。
また、「aᵀ ✕ I = aᵀ」や、「I ✕ Bᵀ = Bᵀ」、「Bᵀ ✕ I= Bᵀ」、「B ✕ I = B」も成立します。
イメージで確認すると、以下となります。



どうでしょうか?
単位行列の意味が掴めたでしょうか?
確かに、入力と同じベクトル・行列が、掛け合わせると出力されるという、面白いカラクリですね。
次に、逆行列ですが、これは、単位行列と密接な関係を持ちます。
数式としては、例えば、行列 A の逆行列は、A⁻¹ と表記します。
そして、行列 A と、逆行列 A⁻¹ とは、掛け合わせると、単位行列 I になります。
つまり、「AA⁻¹ = I」ということです。
逆行列 A⁻¹ は、行列 A を元に算出されます。
ある種、行列 A に対して掛け合わせると、単位行列になるような行列を無理矢理逆算するような形で求められます。
尚、単位行列同様、縦の要素数と、横の要素数とが等しい正方行列です。
イメージとしては、以下です。

こちら、是非、検算してみて下さい。
ちゃんと、単位行列となります。
また、更に面白いことに、「AA⁻¹ = I」だけでなく、「A⁻¹A = I」の関係性も成り立ちます。

こちらも、是非、検算してみて下さい。
リバーシブルな感じで、とても面白いですね。
この辺りが、学問としての秀逸さといえるでしょう。
尚、逆行列の求め方については、なかなか複雑なアルゴリズムを適用する必要があります。
例えば、以下の記事に紹介されていますので、参照下さい。
しかし、コンピューター上で、それを実現する場合には、pythonのnumpyライブラリに実装されている機能を使用すれば、瞬時に算出することができます。
その為、プログラムを用いて計算をする場合には、逆行列を求める計算負荷について、考える必要はありません。
この辺りについては、後ほど説明をします。
さて、線形代数のキャッチアップの最後に、線形代数における計算仕様を紹介します。
それは、計算仕様、及び、計算のルール、及び、計算公式です。
以下のリンクに、それらが全て羅列されています。
リンク先はPDFなのですが、容量が重くロードに時間がかかるので、以下にPDF自体をアップロードもしておきます。
尚、こちらの線形代数の計算仕様については、必要に応じて参照すると良いかと思います。
通常の方程式の操作とは、異なる部分が幾つかあります。
線形代数の何が嬉しいのか?
ここまでで、線形代数の仕組みを説明させていただきました。
さて、この記事の最後に、線形代数の嬉しさについて、言及したいと思います。
線形代数を使うことのメリットを、最も分りやすく体感できるのは、連立方程式の解法です。
連立方程式の一般的な解き方などについては、以下の記事に書いてありますので、良かったら参照下さい。
一般的な解き方は、例えば、中学校の時に学んだ加減法などがありますが、それをプログラムで組むと、結構大変です。
しかし、線形代数を用いれば、それが大変スマートな解くことができます。
例として、上記記事のタイトル画像にもある以下の方程式を解くことにしましょう。

この連立方程式を、線形代数を用いて、解いてみます。
先ず、上記の方程式を、線形代数の表現に落とし込みます。

上の連立方程式で表現していることと、上のイラストで表現していることは同じになります。
さて、イラストの状態について、行列とベクトルを、それぞれ A・b・c と置きます。
線形代数の数式としては、「Ab = c」となります。
ここで、行列 A の逆行列 A⁻¹ を求めて、それを両辺に掛けることにします。
通常の方程式と同様に、同じ行列を両辺に掛けても、方程式の「=」の関係は変わりません。
(※詳細は、matrixcookbookを参照)
尚、両辺に行列を掛ける場合、左辺・右辺のそれぞれにおいて、一番左側に掛けるか、一番右側に掛けるかは、左辺と右辺とで統一しなくてはなりません。
「Ab = c」の両辺に、A⁻¹ を掛ける場合、「A⁻¹Ab = A⁻¹c」か「AbA⁻¹ = cA⁻¹」かのどちらかです。
尚、cA⁻¹ は、計算ができない組合せです。
今回、連立方程式を解くに当たっては、「A⁻¹Ab = A⁻¹c」という計算操作を行います。
ここで、「A⁻¹A」は、単位行列 I となりますので、「A⁻¹Ab = A⁻¹c」という式は、「Ib = A⁻¹c」となり、「b = A⁻¹c」と変換されます。

この時、b は、連立方程式の解である x と y から構成される為、A⁻¹c の計算結果がそのまま連立方程式の解となります。
また、A⁻¹c の計算は、pythonのnumpyライブラリを使えば、簡単に解くことができるのです。
実際に、numpyと線形代数の考えを導入して、連立方程式を解く
それでは、pythonのプログラムでもって、連立方程式を解くエクササイズをやってみましょう。
尚、pythonについて詳しくない方は、以下の記事を読んでもらえると、参考になるかと思います。
(importに関する記事を書く)
先ずは、必要なライブラリをimportします。
必要なライブラリは、numpyです。
import numpy as nppythonで、線形代数や機械学習を扱ったことのある人にとって、上のimportコマンドは、大変おなじみなコマンドになります。
そして、アルゴリズムとして、最初に行うことは、以下の行列とベクトル、A・b・c を定義することです。

プログラムでは、それを以下のように実装します。
行列やベクトルの縦横を整合するように注意します。
import numpy as np
A = np.array([[4, -3],
[3, -7]])
c = np.array([[-9],
[17]])
print('A = ')
print(A)
print('c = ')
print(c)
プログラムの出力結果は、以下になります。
A =
[[ 4 -3]
[ 3 -7]]
c =
[[-9]
[17]]
尚、この時、ベクトル b を定義する必要はありません。
先程の式を見れば分かるかと思いますが、ベクトル b は未知の変数である為、そもそも定義ができず、かつ、逆行列 A⁻¹ と、ベクトル c さえ求まってしまえば、b は自ずと求まってしまう為です。
その為、次に行うことは、行列 A の逆行列を求めることです。
そのプログラムは以下となります。
A_inv = np.linalg.inv(A)
print('A^-1 = ')
print(A_inv)プログラムの出力結果は以下です。
A^-1 =
[[ 0.36842105 -0.15789474]
[ 0.15789474 -0.21052632]]
非常に簡単ですね。
求まった数字については、「ふーん…」という感じですが、計算ステップ自体は、1行で書けてしまいました。
とても簡単ですね。
numpyを実装してくれた方に感謝です。
さて、一応、逆行列が合っているかを確認してみましょう。
逆行列の定義としては、「A⁻¹A = I」と「AA⁻¹ = I」が成立するはずです。
それを確認してみます。
I_tmp = A @ A_inv
print('I_tmp = ')
print(I_tmp)
I_tmp = A_inv @ A
print('I_tmp = ')
print(I_tmp)出力結果は以下です。
I_tmp =
[[1. 0.]
[0. 1.]]
I_tmp =
[[1. 0.]
[0. 1.]]
ちゃんと単位行列になっていますね。
素晴らしい精度です。
尚、行列とベクトルの掛け算については、「@」で表現するのが、numpyの一般的な文法です。
詳細については、以下のオフィシャルページを参考にしていただけたらと思います。
そして、最後に「b = A⁻¹c」を求めます。
b = A_inv @ c
print('b = ')
print(b)出力結果は以下です。
b =
[[-6.]
[-5.]]
以上、解答が求まりました。
一連のプログラムを連結すると、以下となります。
import numpy as np
A = np.array([[4, -3],
[3, -7]])
c = np.array([[-9],
[17]])
print('A = ')
print(A)
print('c = ')
print(c)
A_inv = np.linalg.inv(A)
print('A^-1 = ')
print(A_inv)
I_tmp = A @ A_inv
print('I_tmp = ')
print(I_tmp)
I_tmp = A_inv @ A
print('I_tmp = ')
print(I_tmp)
b = A_inv @ c
print('b = ')
print(b)ここから、print文と、テストコードを除くと…
import numpy as np
A = np.array([[4, -3],
[3, -7]])
c = np.array([[-9],
[17]])
A_inv = np.linalg.inv(A)
b = A_inv @ c
print('b = ')
print(b)となります。
メチャクチャシンプルですね。
これが、線形代数を使うことのメリットとなります。
尚、連立方程式における未知の変数が増えても、上記連立方程式は対応できます。
そして、その延長線上に機械学習の話があります。
以下の記事にその辺りが表現されているので、よければ参照下さい。
(回帰分析と線形代数の記事を書く)
おわりに
以上で、線形代数導入の記事を終えます。
ここまで読んでくださった方、本当にありがとうございました。🙇
おまけ : 逆行列の求め方
逆行列を求めるアルゴリズムについて、C/C++にて実装してくれている素晴らしい記事がありました。
それを、私の方でpythonに置き換えてみましたので、以下参考までに。
# refer from [https://thira.plavox.info/blog/2008/06/_c.html]
import numpy as np
A = np.array([[1,2,0,-1], [-1,1,2,0], [2,0,1,1], [1,-2,-1,1]]).astype(np.float)
A_bk = A.copy()
print('A = ')
print(A)
print()
A_inv = np.zeros([4, 4])
D = len(A)
# 単位行列を作る
for i in range(D):
for j in range(D):
A_inv[i, j] = float(i == j)
# 掃き出し法
for i in range(D):
buf = 1.0 / A[i, i]
print('buf = ', end='')
print(buf)
for j in range(D):
A[i, j] *= buf
A_inv[i, j] *= buf
for j in range(D):
if (i != j):
buf = A[j, i]
for k in range(D):
A[j, k] -= (A[i, k] * buf)
A_inv[j, k] -= (A_inv[i, k] * buf)
# 逆行列を出力
print()
print('A^-1 = ')
print(A_inv)
print()
print('A A^-1 = ')
print(np.dot(A_bk, A_inv))
print()
print('A A^-1 ≒ ')
print(np.round(np.dot(A_bk, A_inv), 10)) # 小数点第10位で四捨五入
