
「まったく美しくない」入門書――近刊『ゲージ理論・一般相対性理論のための 微分幾何入門』まえがき 公開
2021年9月末発行予定の新刊書籍、『ゲージ理論・一般相対性理論のための 微分幾何入門』(佐古彰史 著)のまえがきを、発行に先駆けて公開します。
***
まえがき
本書は一言で表すと、まったく美しくない微分幾何のテキストである。ここでいう「美しい」テキストとは、無駄がなくエレガントに記述されたものであり、本書はそれとは程遠い。なぜ、美しくない教科書を書いたか説明する。
筆者の所属する大学で、おもに理学部の数学科と物理学科の3、4年生に向けて、自分の研究分野に興味をもってもらい、研究室にも入りたくなるような講義をしたいと思って開講したのが「微分幾何入門」である。自分の研究分野であるゲージ場の理論(ゲージ理論といったり接続の幾何といったりいろいろである)や非可換幾何などは、数学科の学生には一通りスタンダードな微分幾何を勉強した先に出会う分野だ。数学科のスタンダードなカリキュラムだと、2年生では曲面論の途中までがやっとで、多様体をしっかり学ぶころには卒業してしまい、学部時代にはゲージ理論などは登場しない。しかし、学生に興味をもってほしいし、自分の研究室に来てほしいので、卒研配属前の3年生をおもな対象とした、1年間でゲージ理論かあるいは一般相対性理論の入門的な内容まで話せる講義を作りたいという野望を抱いてしまった。
講義を始めた最初の年は、小林昭七先生の『接続の微分幾何とゲージ理論』を使い、内容を厳選して講義を構成してみて挑戦したところ、試験では数人が満点近い点数をとったものの、残りの大部分の学生はおおよそ0点になるという恐ろしいことになってしまった。これでは、むしろ研究室の人気が下がってしまうではないか! いかに名著とはいえ、学部の3年生にはハードルが高すぎるし、自分にはそれをかみ砕く実力もないと反省し、学生に寄り添いながら紆余曲折を経て改造していった講義を書き起こしたものが本書ということになる。
結果としてできたものは、抽象的な記述は後回しにして、具体的な座標を使って泥臭く、全然オシャレじゃない計算と説明をして、なんだったらあえて失敗する定義から始めて、悪いところを訂正して説明し、その果てに抽象的な定義にたどり着くスタイルになった。なので、同じことを何度も定義し直したりもするし、いろいろな角度で解釈し直したりもする。具体例も多く、その計算も1年生の微積分や線形代数の具体的な計算に近いものにこだわっている。スマートな記述が好きな、秀才肌の学生にはお薦めしない。どちらかというと、抽象的でオシャレな美しい教科書を読もうとして挫折する学生向けの教科書だ。大学1年生の微積分や線形代数などの必修科目では、高校からの接続を意識して具体的な計算がたくさんある。しかし、それでも大学数学に戸惑っていた学生にとっては、急に抽象的な記述のオンパレードになるとギャップが大きすぎて、自分が学んできたものとつながったものに見えなくなり、挫折してしまうことがよくある。皆が数学者を目指すわけでもないし、他分野が専門という学生もおり、美しいテキストの抽象的な記述をかみ砕く作業にそこまで労力を割けないという事情もあるだろう。美しい数式を見ても、何を意味するのかもつかめず途方に暮れてしまうことになる。たとえるなら、歩いたことしかないのに、急にフェラーリでサーキットを走れといわれても途方に暮れるようなものだ。なので、とりあえずランニングから始めてサーキットに慣れてから、自転車で走ってみようというのが本書のコンセプトである(ちなみに、筆者はフェラーリを運転したことはなく、もしかしたらとても運転しやすい可能性はある)。
本書で仮定されている数学の知識は、大学1、2年生の微積分、線形代数だけである。ただし、線形代数については、計算ができるだけではなく、線形写像の抽象的な概念について既知としている。ベクトル解析や曲面論が既習だとわかりやすい部分や、群とか位相という言葉を知っているとより深く理解できる部分もあり、それらを知る読者向けのコメントもしているが、それらの予備知識がなくても十分読み進められるようにしてある。本書のもとになった実際の講義では、物理学科の学生も多く履修していて、位相や代数の講義を履修している学生だけが対象ではないからだ。一方で、多様体の基礎から始め、微分形式やファイバー束などを経て、ゲージ理論や一般相対性理論にいたるまでの微分幾何の広い範囲の内容を1年間の講義で学ぶ設計にしているために、スタンダードな教科書ではやるべき内容でも、直観で納得できるところは触れずに通過していることがある。たとえば、多様体を導入するにあたっての位相(連続性)についての議論はほんの少ししかない。ε-δ論法による連続の定義を知らなくても、高校で微積分も勉強したし、そもそもニュートンやライプニッツも、位相やε-δ論法は知らなかったのと同じように、これらについての子細な議論は必要になった人だけ後で個人的に穴埋めしてもらって、進んでしまえという作戦だ。
ところで、タイトルに入っている言葉で相対性理論のほうは聞いたことがある読者が多いかもしれないが、ゲージ理論のほうは初耳の方もいるかもしれない。ゲージ理論は微分幾何の一分野であるという面もあるかもしれないけれど、ゲージ理論は皆さんの身の回りのすべてであるという言い方もできる。というのは、物理学の基本法則は重力理論、電磁気学、それと2種類の核力の理論からなっていて、それらはすべてゲージ理論であるからだ。体重計に乗って自分の体が地球の重力にどれくらい引っ張られているかという測定や、ホームランの打球がどれくらいの距離で落下するかという身の回りのことから、太陽の周りを回る地球の公転や、ブラックホールや宇宙の膨張にいたるまで、宇宙の様子を記述するのが重力理論である。これは一般相対性理論で記述されるが、これもゲージ理論である。照明やスマホに関することから、われわれの生命活動や化学変化などを含めて、身の回りの大部分の現象は電磁気学の理論で記述されるが、これもゲージ理論である。さらに、原子力や太陽で起こる核融合のような現象を担う核力の理論も、ヤン-ミルズ理論などのゲージ理論から説明される(ただし、それらの量子論の部分は本書では一切扱わない)。ゲージ理論は幾何学の中で「接続の幾何学」とよばれるものであり、ファイバー束とよばれる多様体の上で微積分を考える理論である。微分幾何の基礎事項を修得しながら、ゲージ理論の入門的な話題にまでいたることが本書のおもな目的である。単に数学的な内容で終わらず、せっかく学んだ微分幾何が身の回りの物理現象をどのように説明するかということまで知ることで、より興味をもてるかもしれないと考え、電磁気学やヤン-ミルズ理論、重力理論である一般相対性理論について、まったく物理学を知らない読者を対象にした解説も含んでいる。
本書の章ごとの関係は、以下のようになっている。
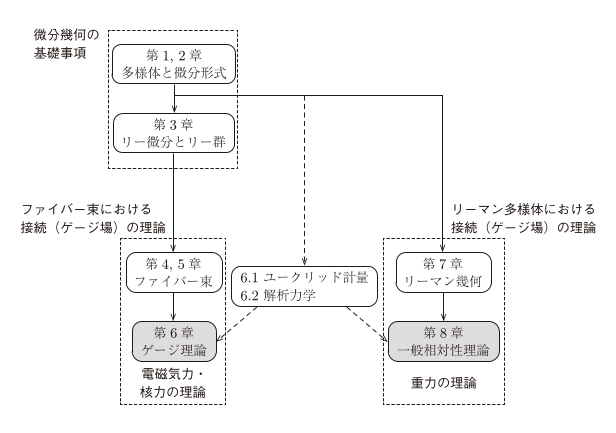
後半の部分はなるべく独立して読むことができるように書いた。一般相対性理論を理解するだけなら、第1、2、7、8章を読むだけでよい。第6章のはじめの2節についても独立に読むことができ、それも第8章の理解の助けになる。
本書の執筆のもととなった講義は、最初の出発点として、小林先生の教科書を使っていて、また具体例などの説明を中原幹夫先生の『理論物理学のための幾何学とトポロジーI、II』から採用していた。そのため本書でも、論理展開や具体例はこれらにならっているところが多い。無理に書き換えることはむしろ質を下げたり、本書からそれらの名著にステップアップする際に対応が見にくくなるので、やめることにした。いずれにしても、幾何を学んだことがある人なら誰でもよく知っている微分幾何の古典的な内容だけを扱い、広い範囲の大事なアイディアを厳選し、少ない予備知識でそれらに入門することが本書のおもな目的なので、そこに注力した。あくまでも名著に当たる前に、あるいは名著にチャレンジして挫折した際に、高校数学のように計算で手を動かせるようになりながら、抽象的な記述に慣れていくというような使い方をしてみてもらえたらと考えている。読んでみて、微分幾何が面白そうだ、あるいは微分幾何でさまざまな物理現象を記述できることが面白そうだ、と思った読者がいてくれれば望外の喜びだ。一方で、こんな泥臭く計算した汚い数学書はけしからんと思う読者がいたとすると、この本がたまたまそうであって、ほかの教科書は決してそんなことはないので、この本がきっかけで微分幾何を嫌うようなことがないようにと、切に願っている。
佐古彰史(さこ・あきふみ)
東京理科大学理学部第二部教授、博士(理学)。著書に『超対称ゲージ理論と幾何学―非摂動的アプローチ』(日本評論社)、『幾何学の量子化―変形量子化からのアプローチ』(サイエンス社、共著)、『非可換微分幾何学の基礎』(共立出版、共著)がある。
***
『ゲージ理論・一般相対性理論のための 微分幾何入門』
https://www.morikita.co.jp/books/mid/007851
【目次】
第1章 多様体
1.1 多様体
1.2 接ベクトルと接ベクトル束
第2章 微分形式
2.1 線素,面積素,体積素
2.2 外積と外微分
2.3 微分形式の積分
2.4 ド・ラームコホモロジー
2.5 押し出しと引き戻し
第3章 リー微分とリー群
3.1 積分曲線とベクトル場の流れ
3.2 リー微分
3.3 リー群とリー代数
3.4 線形リー群
第4章 ファイバー束
4.1 接ベクトル束TM
4.2 ファイバー束
4.3 ベクトル束
4.4 ベクトル束の接続
4.5 ベクトル束の曲率
第5章 主束
5.1 主束Pの構成
5.2 同伴ベクトル束
5.3 押し出しと引き戻しの復習
5.4 接続の幾何学的構成
5.5 エーレスマン接続とゲージ場(接続1-形式)
第6章 ゲージ理論
6.1 ℝᴰにおける計量とホッジ作用素
6.2 解析力学
6.3 場の作用
6.4 ゲージ理論 ―場の理論の対称性から
6.5 マクスウェル理論:U(1)ゲージ理論
6.6 ヤン-ミルズ理論の解(インスタントン)
6.7 特性類
第7章 リーマン幾何
7.1 部分多様体
7.2 平行移動と共変微分
7.3 部分多様体M⊂ℝᴺの接続
7.4 リーマン多様体の接続と曲率(局所標構場を用いて)
7.5 リーマン多様体の接続と曲率(一般の座標で)
第8章 一般相対性理論
8.1 解析力学と保存則
8.2 重力場中の質点の軌跡と測地線
8.3 重力場の方程式
8.4 球対称解
8.5 球対称な空間の物理
問題解答
参考文献
索引

