
近刊『位相空間論―現代数学への基礎―』まえがき公開
2021年3月下旬発行予定の新刊書籍、『位相空間論』のご紹介です。
同書のまえがきを、発行に先駆けて公開します。
***
『位相空間論―現代数学への基礎―』まえがき
現代数学は多くが連続の概念に基づいている。そのため現代数学を理解し、記述するためには位相の概念を学ぶことは不可欠であり、数学や物理学を専攻する学生諸君向けに「集合と位相」、「位相入門」などの科目が開講されている。しかし、それらの授業でこれまで何気なく使ってきた内容を論理的に説明され、一般化された新しい概念を定義されても、その意味合いと直感的な概念との結びつきがつかめないことが多いようである。
本書は、筆者が早稲田大学基幹理工学部応用数理学科2年生に開講している「集合と位相」の授業で用いている自筆テキストを修正、加筆したものである。様々な位相に関する入門書が出版されているが、その多くが授業の補足解説や試験対策に力点が置かれ、実際に「位相空間論」を使うにはときには不十分なものとなってしまっているきらいがある。本書は直感的な概念と論理的な概念との関係が明確になるように努めているが、「位相」の授業を乗り切るためだけではなく、上級生になったときにも使える「現代数学の基礎」になり得る教科書を目指している。
第1章では、直感的にとらえやすいn次元Euclid空間や微分積分学で使われてきた内容から距離空間の概念を導入して、位相の概念を導入する理由をわかりやすく書き下した。ここで様々な例を挙げ、直感的な理解を論理的な理解へ発展させることと詳しい証明を記すことで、第2章の位相空間への展開が容易に理解できるように工夫した。第2章では証明を省略していることが多いが、第1章を参考に自分で証明を付けてほしい。第1章では、一般的な定義や定理から天下り式に例を説明することを避け、平易な例や事項から一般的な事項を導く考え方が明確になるように努めている。そのため多少の重複があるが許容してほしい。第3章では初学者には取り扱いが難しい直積空間について、はじめに有限個の因子空間からなる直積空間を取り上げ、次に無限個の因子空間の直積空間を取り上げている。無限個の距離空間の直積空間についても距離付け可能性、直積位相との関わりを解説した。商位相や商写像について、接着空間の位相が理解できるように、また可分とは限らない距離空間の分割空間の距離付け可能性を議論できるように心がけた。
本書は位相空間論の高度な専門書ではないので、距離空間と関連する諸定理を中心に解説している。そのために、コンパクト距離空間と完備距離空間について独立の章を設けて、多面的な見方を示している。距離空間におけるコンパクトの定義は、Bolzano–Weierstrassの定理に基づく点列コンパクトを採っている。第5章では(この意味での)コンパクト距離空間の性質を詳しく調べ、開被覆を用いる位相空間のコンパクト性の定義と同値になることを示す。この方法は一般的ではないが、距離空間でものごとを考える場合には汎用性が広く、また一般化への道筋を示すよい方法と考えている。また、道具としての位相空間論を学ぶだけではなく、可分距離空間の幾何学も体験してほしいと考え、Cantor集合の性質(第8章発展2)やPeano写像の存在(第9章発展3)を取り上げた。代数的トポロジーで用いられる位相空間論を意識して、ホモトピー拡張定理のアイディア(第4章発展1)や商写像の直積写像に関するWhiteheadの定理(定理6.25)にも言及している。最終章では、Banachの縮小写像定理の応用例としてJ.Hutchinsonが導入し、M.Barnsleyらが応用へ展開しているフラクタル集合の構成法(iterated function system)を紹介している。この章を読み進めると、それまでの諸結果が縦横に使われることを実感できるだろう。
本書を一学期の教科書として使う場合、距離空間とそこから導かれる位相の概念を中心に、下図の点線枠の範囲で利用することを推奨する。
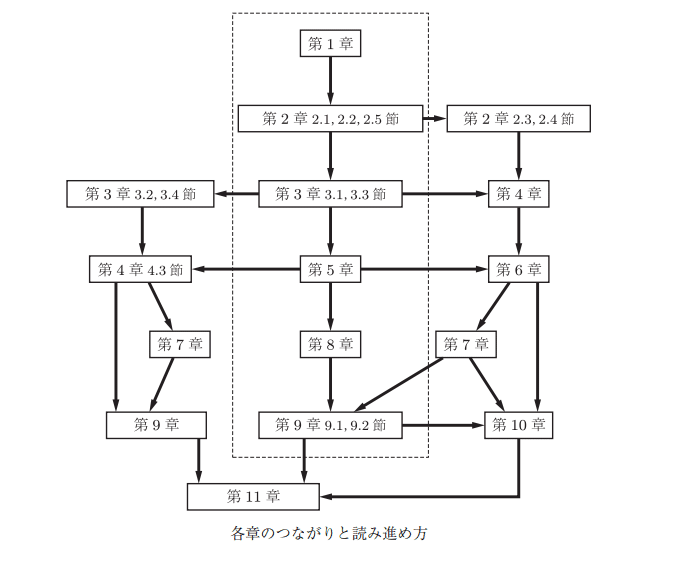
この場合、主に因子空間が有限個の直積空間に限られる。ただし、可算無限個の距離空間の直積空間に言及したい場合も考慮し、可算無限個のコンパクト距離空間の直積空間がコンパクトであることの初等的証明を与えているので参考にしてほしい。
一方、第4、6章は発展的な内容を含んでいる。また第7、10章は通常の授業範囲を超えているが、もう一段階に進んだ数学を学ぶ場合には必要になるものである。実際、第7章では、解析学などで局所的な性質を大域的な性質へ拡張するときに重要な役割を果たすパラコンパクト空間の性質を解説し、1の分割の存在との同値性を示していく。また、距離空間がパラコンパクト空間であることを示したStoneの定理(定理7.1)や長田–Smirnovの距離付け可能定理(定理7.3)に取り組んでいる。さらに、第10章では関数空間の位相についても体系的に解説する。そこではコンパクト開位相の役割を解説し、同相群の位相に言及している。
筆者は集合論的な位相空間論の専門家ではないので、全般的に証明は素朴な考え方に基づくものである。そのため、特に第4章、第6、7章の証明などは現在の位相空間論の進展から見ると冗長なきらいがあるだろう。しかし、位相空間論をより深く学びたい諸君には、アイディアに触れるよい機会になると確信している。また、位相空間論に関心をもった諸氏の独習の手助けになればと、練習問題に略解とヒントを付けた。略解は一つの考え方であり、読者諸氏が自分自身の解答を付け、理解を深めてもらえれば幸いである。
***
『位相空間論』
https://www.morikita.co.jp/books/book/3596
著:小山晃
位相空間論の基礎を学び、そこから見える数学の世界にも触れられる入門書。
豊富な例を取り入れ、直感的な理解が論理的な理解に結びつくよう配慮しながら、丁寧な解説がなされています。数式を示すばかりではなく、「なぜこの概念を考えるのか」「なぜ一般化するのか」といったことも書かれているので、位相の面白さや有用性を感じながら読むことができます。
やや発展的な内容として、解析学などで重要となるパラコンパクト空間の性質を解説しています。また、可分距離空間の幾何学や代数的トポロジーについても言及し、最終章ではフラクタル集合の構成法も紹介しています。
多くの練習問題と解答も掲載。
現代数学を学ぶうえで役立つ、充実の一冊です。
【目次】
第1章 距離空間
1.1 準備
1.2 距離関数と距離空間
1.3 点列の収束と極限
1.4 距離空間と位相
1.5 部分空間と直積空間
1.6 極限点,閉集合,閉包
1.7 集積点,閉包,内部
1.8 連続写像
1.9 いろいろな連続写像
1.10 同相写像
1.11 付記 : H¨olderの不等式とMinkowskiの不等式
第2章 位相空間
2.1 近傍系と位相
2.2 開基と部分開基
2.3 部分空間
2.4 集積点,閉包,内部
2.5 連続写像
第3章 直積空間と商空間
3.1 直積空間—その1:有限個の空間の直積空間
3.2 直積空間—その2:無限個の空間の直積空間
3.3 無限個の距離空間の直積空間
3.4 商空間と商位相
第4章 分離公理
4.1 分離公理—その 1:定義と基本的な性質
4.2 分離公理—その 2:正規空間の性質
4.3 可算性と距離付け可能性
第5章 距離空間—その2:コンパクト距離空間とその性質
5.1 コンパクト距離空間—その1:定義と基本的な性質
5.2 コンパクト距離空間—その2:特徴付けと開被覆
第6章 位相空間—その2:コンパクト空間とその性質
6.1 コンパクト空間
6.2 Tychonoff立方体の性質—その1:Tychonoffの埋め込み定理
6.3 Tychonoff立方体の性質—その2:Tychonoffの定理
6.4 局所コンパクト空間
6.5 商空間と商写像
第7章 位相空間—その3:距離空間とパラコンパクト空間
7.1 距離空間の開基と距離付け可能定理
7.2 パラコンパクト空間と1の分割
7.3 距離空間とパラコンパクト空間の分割空間
第8章 連結と道連結
8.1 連結
8.2 道連結と局所連結
第9章 完備距離空間
9.1 完備距離空間—その1:定義と基本的な性質
9.2 完備距離空間—その2:特徴付けとBaireの定理
9.3 完備距離空間—その3:距離空間の完備化
第10章 関数空間の位相
10.1 関数空間—その1:一様収束位相と各点収束位相
10.2 関数空間—その2:コンパクト開位相
10.3 関数空間—その3:Ascoli–Arzel`aの定理
第11章 超空間
11.1 超空間の定義と基本的性質
11.2 和集合写像と縮小写像
11.3 Hausdorff距離とVietoris位相
11.4 応用—フラクタル集合の存在
練習問題のヒントと略解例
参考文献
索引

