5分でわかる重回帰分析 応用編〜ロジスティック回帰分析〜
こんにちは、森です。
先日書きました、「5分でわかる重回帰分析 基礎編」の続きとして、今回はロジスティック回帰分析について簡単に説明していこうと思います。
ロジスティック回帰分析は
目的変数が質的変数、説明変数が量的変数
の多変量解析を行う際に非常に有用です。
成約するかしないか、合格可能性などの確率を求める際に使用されます。
ロジスティック回帰分析は重回帰分析と異なる下記の計算式で表されます。
y=1/(1+exp(-(b1*x1+b2*x2+b3*x3+・・・+bi*xi+b0)))
y:目的変数(確率)
x1, x2, x3,・・・, xi:説明変数
b1, b2, b3,・・・, bi:偏回帰係数
b0:定数
重回帰分析の計算式に比べてもやや複雑で、それぞれの係数を求めるのは手計算では困難です。
通常、Excelにはロジスティック回帰分析を行うツールが搭載されておりませんが、ソルバーを使うことによって最尤法で解析を行うことができるので、そちらの方法をご紹介いたします。
今回も私が適当に作成した下の表を使って、「初体験が18歳以下である確率」を判定するモデルを作成してみたいと思います。
最終的な目標は「男, 顔面偏差値50, 男子校出身, 友人の数15人」の人の「初体験が18歳以下である確率」を求めてみます。

まずはこの表を分析できる形に整理します。
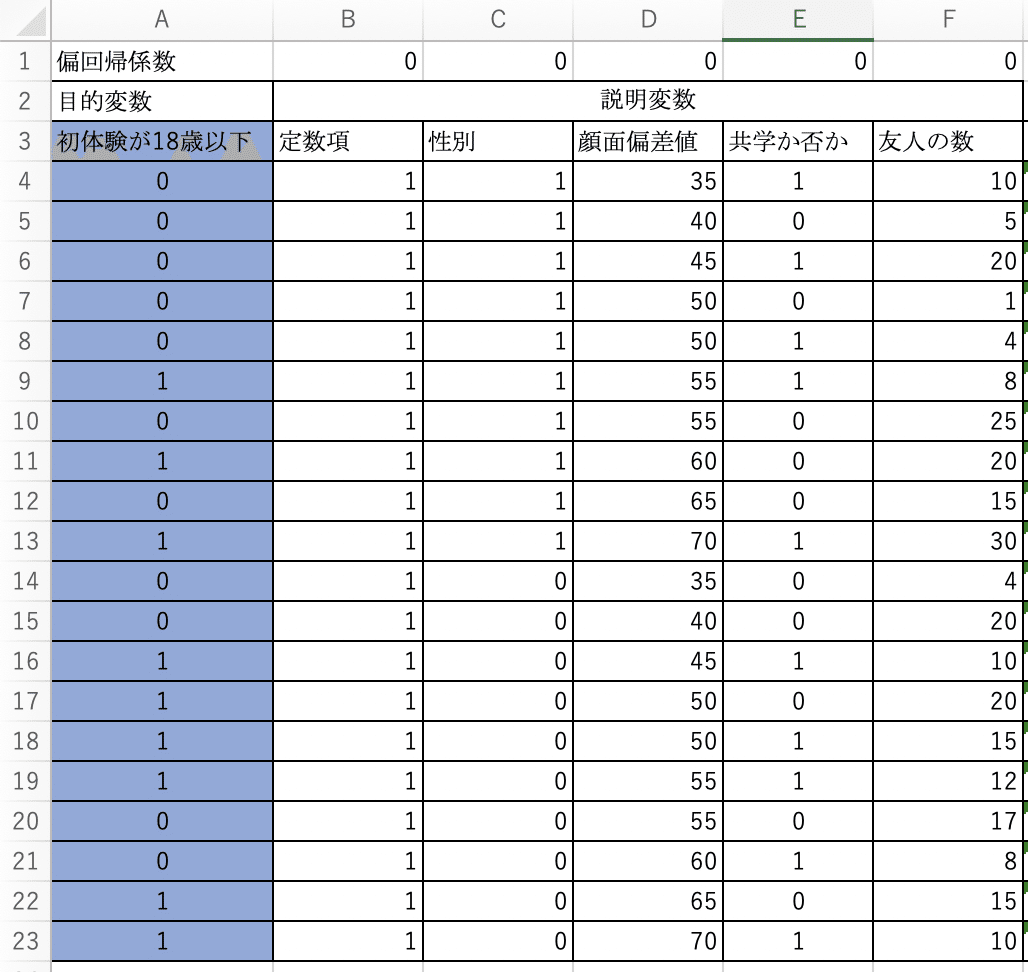
目的変数と説明変数の中の質的変数をダミー変数へと直します。
「○」で表現していたものを1、空白を0とします。
そして、説明変数の列に定数項を加えておきます。
一番上の行は「偏回帰係数」とし、とりあえず0を入れておきます。
ソルバーを使うことによってこの0が入っている偏回帰係数を自動で調整してもらいます。
次にそれぞれのデータの推定値の列を作成します。

推定値は、最終的に出来上がったモデルに各行の数値を代入した際の結果が吐き出されてくる項目です。
ですので、例として4行目の推定値は
=1/(1+EXP(-SUMPRODUCT($B$1:$F$1, B4:F4)))
となります。これを各行に適用します。
現状はソルバーで偏回帰係数の調整を行なっていないので、全ての行が0.5になっていますが、大丈夫です。
続いて、データごとの対数尤度を計算し、モデルの対数尤度を算出します。

例として、4行目のデータの対数尤度は
=A4*LN(G4)+(1-A4)*LN(1-G4)
で求めることができます。
全ての行が-0.693147181となっていますが、ここまでの手順はどんなデータを使っていてもこうなるので大丈夫です。
そして、適当なところにデータごとの対数尤度の合計の-2倍を算出するセルを作成します。

ここまでで準備完了です。
ソルバーを用いて、この対数尤度の-2倍の値を最小化するように偏回帰係数を最適化してもらいましょう。
「データ」タブの「ソルバー」をクリックします。
「ソルバー」が表示されていない方はExcelアドインの設定からonにする必要があります。

目的セルの設定:対数尤度の-2倍のセルを指定
目標値:最小値
変数セルの設定:変回帰係数の行(0が入力されているところ)
制約のない変数を非負数にする:フラグいれない
解決方法の選択:GRG非線形
と設定し、「解決」します。
特に問題がなければ数秒で収束し、下記のように対数尤度と偏回帰係数が最適化されます。

ということで、偏回帰係数を求めることができました。
モデルは下記のようになることがわかります。
y=1/(1+exp(-(-1.79*x1+0.127*x2+2.20*x3+0.122*x4-8.92)))
y:初体験が18歳下である確率
X1:性別(男なら1, 女なら0)
x2:顔面偏差値
x3:共学か否か(共学なら1, そうでなければ0)
x4:友人の数
行13の男性、顔面偏差値70, 共学, 友人30人のかたは
推定値:0.982
となっており、作成したモデルにデータを代入した時に、
「初体験が18際以下である確率が98.2%」
と算出されることがわかります。
それでは目標であった
「男, 顔面偏差値50, 男子校出身, 友人の数15人」の人の「初体験が18歳以下である確率」
を求めてみましょう。
代入するだけです。
0.0738=1/(1+exp(-(-1.79*1+0.127*50+2.20*0+0.122*15-8.92)))
ということで18歳で初体験を済ませている確率が7.4%であると算出されました。大学入学時点では童貞のタイプですかね。
まぁ、私が適当に用意したデータなんで意味はないのですが笑
と、いうことでロジスティック回帰分析をExcelで行なってみました。
少しややこしいですが、慣れてしまえばそんなに難しいものでもないので、何かの確率を複数のデータから求める際にはかなり使えるはずです。
それでは、また。
