具体か抽象か。考え方のクセを見抜け

こんにちは。ゼロです。サラリーマンです。
何者でもない一般人の私の発信が前向きに成長しようともがいている同じようなあなたに届けば嬉しいです。

さて、子どもに勉強を教えていてブチ切れた話の続きです。
前の記事を読んでない方は是非読んできてください。
なぜか今回のタイトルがかっこつけがちになってますが先ほどの続きです。

前回はこちら
↓
子どもにブチ切れたアホの話
なんでこんなこともわからへんねや！

子どもに風呂の鍵をかけられ一人寂しく寝ました。

教えてたのか？ただ、キレてたのかよくわからない状況になってしまったことを反省して目覚めました。

ひとまず、子どもに謝ろう。
「昨日は、怒ってごめんなさい。これからは教えても怒らないようにするから」
まあ、いいよ。といってもらって、その夜

お父さん一緒に勉強しよ

と言ってもらえたので泣ける

ちゃんとしよ（キレてはいけない）

というわけで、勉強の続きです。
まず、情報の整理です。

子どもは何につまづいているか？
（わからないところはどこか）
※画像を再び
わり算の筆算をするときに、答えを右に書いてしまう。

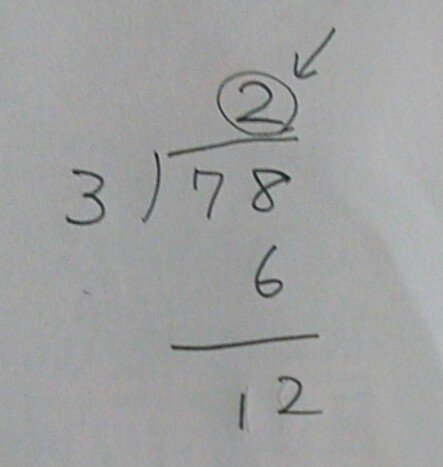
ポイント②点です。

①子どもは右側に書いてしまうこと

②私にはなぜ右側に書くのかわからない

特に②が重要で、私には、わり算の筆算って左から書くと教科書に書いてある以上、なぜ右側に書いてしまうのか全くわからない。

あっ！わり算ってこっちからなのね

と、特に深く考えずに出来てしまう。1と2を聞けば3とか4までわかる。どうやら、これは抽象化して考えている。（らしい、しらんけど）

自分が小学3年生の時の記憶はないけれど、なぜ左から書くのか？ということをこれまで考えたことはない。

これが、このまま昨日のセリフにつながったわけです。

なんでこんなことがわからへんのや！！

答えは抽象化できないから。ということであれば具体に落とし込んでいかないといけません。
私の見立てはそうなったので、子どもに聞いてみました。

なぜ、右側に書くの？

答えは私には思いつかないものでした。

「かけ算も足し算も引き算も筆算は全部右からやん。」

なるほどねーーーーっ！！
（あっ、そういうことですか。そうとわかれば話が早い。（この辺りが抽象化の思考なのかもね。しらんけど））
というわけで、子どもにもう一つ質問してみた。

「この問題わからないんだよね。これをやるとき、何を思い出してやった？？」

「前回の塾の授業（かけ算）」

はい。ビンゴ。（ようやく、なぜ子どもが右側に答えを書くのか謎がとけました。）

わり算の筆算をかけ算の筆算を思い出しながら解こうとしていたのです。

かけ算の筆算は右から答えを書いていきます。
どうやら、息子ちぁんは、筆算は右から、答えを書くと覚えていたようです。

では、参考書を見ながら復習すれば良い。
筆算の見本を全部みます。
足し算の見本
引き算の見本
かけ算の見本
わり算の見本

それぞれの答えの書き方は？

足し算。右から　
引き算。右から　
かけ算。右から　
-------------------------
わり算。左から

わり算のやり方と他のやり方、関係ある？
関係ないよね。わり算をするときに他のことを参考にしてはいけないよ。

わり算は仲間はずれだから
筆算の形も違うでしょ。

わり算は仲間はずれ

という言葉で具体的に、わり算とかけ算を切り離しました。

やり方は違うよ。ということを意識させます。
迷ったら　わり算は仲間はずれ　と言おう。
これを何度も繰り返してどこに答えをかけばいいかわからない問題はクリアできました。

私も何でそんなことがわからんへんのや
ということなく、課題を具体化することに集中しキレずに教えることができました。

なるほど、息子ちぁんは、具体の思考をするのね。

４人家族ですが、たぶん、一つ一つを具体的に理解していきたい具体の思考をするのは息子ちぁんだけだと思われ、だからこそより教えにくいということが発生していました。

典型は娘ちぁん。いま、算盤でこんな問題をしています。

なんで、できるの？って聞いたら

アタマの中にコビトがおるやろ！
そのコビトに教えてもらったらええだけやろ！

となんだかよくわからないことを言っていました。
ちなみにそのコビトはよく寝るらしいっす。
※33番の時は寝てたのかな。コビト
具体と抽象というレベルを越えとる

さて、次に復習でかけ算の筆算をやってみたところ、困ったことにやっていました。
↓こんな感じ

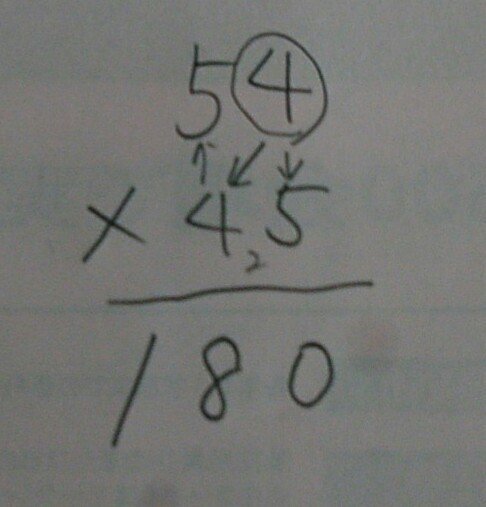
※画像は私が計算したものです。

最初に　５×４　２あがって　５×５といきたいとのろですが、４×４をしているようです。

ん？なんでそんなことになるん？

といいたいですが、よくよくみると
たすき掛けで計算しているようです。

上の問題だと　２８８０　という答えになります。
※正解は2430

昨日だと間違いなくブチ切れているところですが
具体化しないとわからない。という考え方のクセをわかっているので一つ一つ噛み砕いて説明を行いました。

筆算のかける順番はそれであってるかな？
どういう順番で計算するか、自由自在（参考書）で見直そうか？

参考書のかけ算の筆算のページを開いて何度も何度もかける順番を見直しました。

よし！できるようになったやん！！
塾のテスト頑張れ。
その日のテストは衝撃の３３点！！

天才じゃん！！伸びしろしかない！

勝手に自分で想像（考え）して、すすめていく抽象の思考をするのか

一つ一つ確実に理解しながら、すすめていく具体の思考をするのか

考え方のクセを見抜けばその人にあった教え方ができるようです。

ここに気づくまで、まわりの人が抽象化思考がめちゃくちゃ得意で、1いえば10理解するような人材なので、自分が教えるの得意だと勘違いしてました。

本当に申し訳ございません。

周りが優秀なだけでした。

あの人、物覚えわるい！理解わるい！

とか、ほんの少しでも感じてしまった場合は
相手の考え方のクセと自分の考え方のクセの差を考えてみれば、前にすすめるかもしれません。

あくまでどっちがいい悪いとか上とか下とかではなくて、考え方の違いなので、相手がどうなのか
を考えたほうがいいよねっていうお話。

えっ、自分がどっちかってどうやったらわかるかって

そんなもん考えたらすぐわかるだろ

もし、↑こう思ったなら、こういう風に具体的事例がなくても理解できるのが抽象思考かと。

いや、そうじゃなくて、理由と解説と具体的な見分け方をって思ったら具体思考じゃね？
#しらんけど

今日もハッピーな１日を
がんばろうね。
ぼくもがんばります。
毎日、修行中

では、またね