TOC（制約理論）まとめ　スループット会計4

TOC（制約理論）の知識定着を目指し、学習したことをアウトプットしていきます。今回はスループット会計の完結編です。
スループット会計を理解する上で、活動基準原価計算（Activity Based Costing）と線形計画法は抑えておきたいです。今回は、前回の活動基準原価計算に続き線形計画法についてまとめていきたいと思います。
なお、シリーズ最初の記事はこちらです。

「スループット会計」と「間接費を配賦する原価計算」との比較

TOCは利益最大化のアプローチとして、スループットの最大化を最優先にしています。これは間接コストを製品に配賦して原価を算出している現在主流の原価計算からすると少しとっつきにくい感じもします。
簿記の教科書を確認してみると「直接配賦」や「間接配賦」など配賦という考え方がいたるところに出てきますので、間接費を配賦するというのは一般的な考え方として定着している印象です。
しかし、「現在主流の原価計算はダメなのか？」と聞かれればまったくそんなことはありません。そもそも、原価計算（管理会計）は何かしらの目的があって導入されます。どのような原価計算方法であっても目的が満たせるのであれば問題ないと思います。そう考えると、TOCも管理会計における1つのアプローチであり、どちらが正しいのかという議論をするのはナンセンスだと思います。

スループット会計は線形計画法で表現できる

どちらが正しいかという議論はナンセンスですが、それでも比較はしてみたいものです。私もいろいろと調べたり、自分なりに考えてみました。その結果、スループット会計でやっていることは、線形計画法（リニアープログラミング）で表現できることに気付きました。線形計画法は、簿記の教科書にも載っていますので、一般的な管理会計でも使われている理論です。スループット会計でやっていることも一般的な原価計算で説明できるということになります。

線形計画法（リニアープログラミング）とは

簿記1級の「最適セールス・ミックス」で登場します。制約条件が2つ以上ある場合に営業利益を最大化する各製品の販売量の組み合わせを求める手法になります。以降は例題を用いながら線形計画法について説明していきます。

線形計画法の例題

説明で利用する例題について、まずは前提条件を整理します。

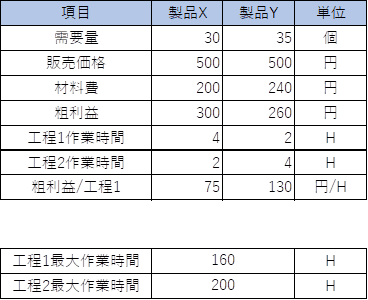
ある企業では、製品Xと製品Yの2種類を製造しています。どちらの製品も工程1と工程2を通過します。工程1の最大作業時間は160H、対して工程2の最大作業時間は200Hです。
工程1、工程2は、製品ごとに加工時間が変わります。製品Xを製造する場合、工程1で4H、工程2で2H必要になります。対して製品Yの場合、工程1で2H、工程2で4H必要になります。
ここまでの条件を整理すると、最大作業時間が短い工程1がボトルネック工程になっていることがわかります。

さて、これを線形計画法で表現してみます。

工程1の生産能力グラフ

グラフを確認してください。これは、工程1の製造能力をグラフにしたものです。工程1は、製品Xを製造する場合は4H、製品Yを製造する場合は、2H消費します。最大作業時間は160Hです。これを不等式にした場合、下記になります。

4x+2y≦160

この式をグラフにしたものが「Graph1」になります。
求め方は簡単です。

まず、4x+2y≦160の式に対して、yに0を代入すると、xは40になります。

4x+2(0) ≦160　→　x≦40

yに0を代入するということは、製品Yをまったく製造しなかった場合の製品Xの製造量を求めたことになります。
これを座量に記入します。グラフの下側、(40,0)の位置です。

次に、4x+2y≦160の式に対して、xに0を代入します。そうすると、yは80になります。

4(0)+2y ≦160　→　y≦80

これを座標に記入します。(0,80)の位置です。
この2つの座標を線で結んだものが、工程1の生産能力になります。
このようにして、グラフを作成していきます。

工程2の生産能力グラフ

次は工程2の生産能力グラフを作成します。

Graph2を確認してください。2x+4y≦200を追加しました。こちらは、工程2をグラフにしたものです。算出の仕方は、工程1と同じです。
工程1と工程2の線が交わった個所が、最適な生産数量になります。ただし、これは市場の需要量に制限がなかった場合です。今回は各製品に需要上限数が設定されていますので、この交点は利用できません。

製品Xの需要量

製品Xの需要量は30個が上限でした。そのため、グラフにも制約を追加します。
x≦30
グレーの線が垂直に入りました。

製品Yの需要量

製品Xと同じように、製品Yにも需要上限があります。グラフにも製品Yの制約を追加します。
y≦35
オレンジの線が水平に入りました。

外角のどれかが最適生産になる

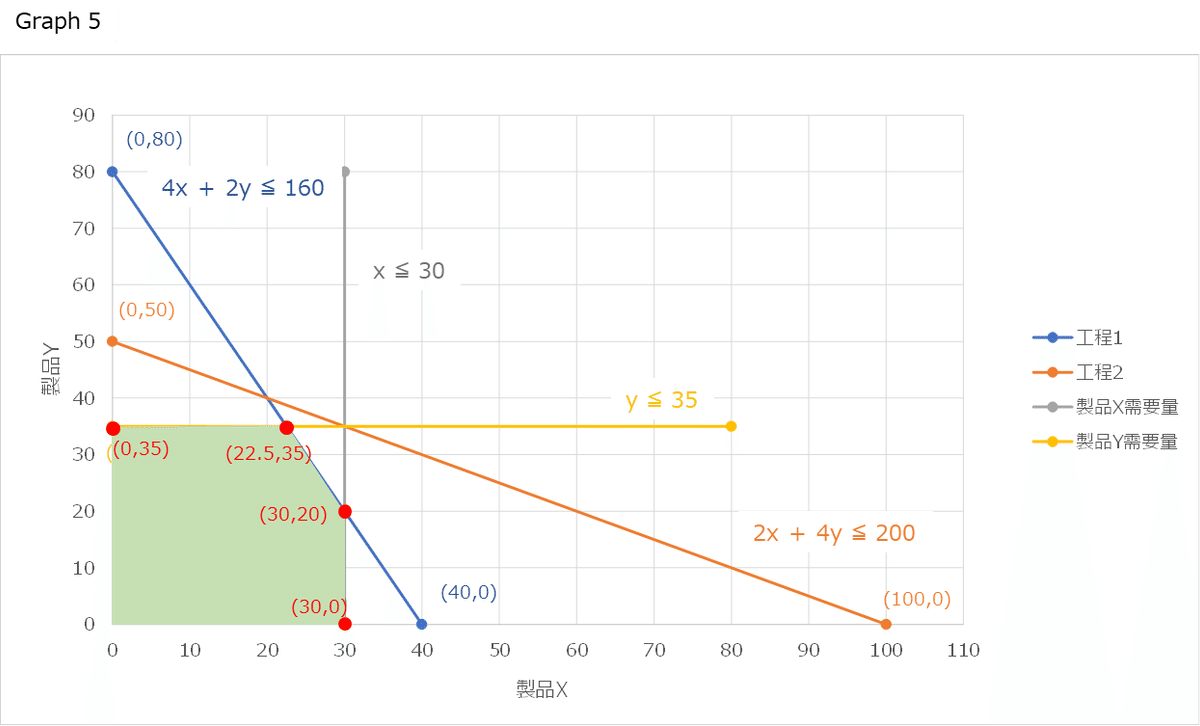
すべての制約条件を線にすると、生産数量の決定で選択可能な領域が明らかになります。ちょうど、緑の領域です。この領域の外角にある4点が最適生産数の候補になります。ここまで来たら、4点の利益を算出してみます。粗利益×生産数量で計算します。
なお、座標(22,5,35)の22.5は切り捨てて、22として考えます。

(0,35)  　(300円 × 0個) + (260円 × 35個) =9,100円
(22,35)　(300円 × 22個) + (260円 × 35個) = 15,700円 →最適生産数
(30,20)　(300円 × 30個) + (260円 × 20個) = 14,200円
(30,0)  　(300円 × 30個) + (260円 × 0個) = 9,000円

製品Xを22個生産し、製品Yを35個生産するパターンが利益を最大化することがわかりました。
これが線形計画法になります。

スループット会計で考えると

スループット会計で考えるとどうなるか復習してみます。
ボトルネックは工程1になります。そのため、工程1を1H消費した際に得られる粗利益を求めます。工程1は75円/Hです。対して工程2は、130円/Hになります。

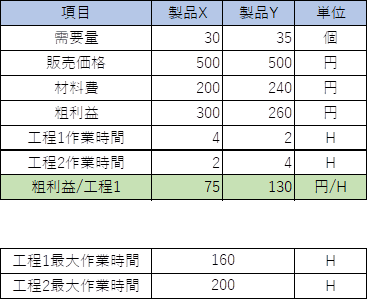
スループット会計では、製品Yを優先的に生産し、余った余力で製品Xを生産することになります。
そうすると、製品Yを35個生産し、製品Xを22個生産することになります。
これは、線形計画法で求めた答えと同じになります。

スループット会計でやっていることは、線形計画法と同じです。スループットの最大化を図る際には、線形計画法のアルゴリズムで計算すれば再現できるはずです。

変数が2つ以上の場合

スループット会計を線形計画法で再現しました。しかし、今回紹介した線形計画法は変数が2つの場合のみしか対応しません。なぜなら、製品が2つ以上の場合は、グラフで表現できないからです。
製品が2つ以上ある場合は、Excel等の関数を使うことで求めることができます。Excelだとソルバーという関数になります。こちらの説明は他のサイトに委ねますが、線形計画法でスループット会計で用いている「スループットの最大化計算」が可能であることを理解して頂ければと思います。

最後に

なんだか、長くなっていしまいましたが、4回に分けてまとめてきたスループット会計も、このあたりで終わりにしたいと思います。
自身の理解を深めるために、壁打ちのようにスループット会計をまとめてきましたが、多少でも読んで頂いた方々のお役に立てているようならうれしく思います。
それでは、最後まで読んで頂いてありがとうございます。

Twitterやってます。
フォローいただけると嬉しいです。
https://twitter.com/Mick_Consult