高校生でもわかりそうだけど、ちゃんと理解もするUnityでのクォータニオン運用法

Unityでゲームを作ってる人ならなんとなく聞いたことはあると思います。

クォータニオン。

あいつはなんなのだろう。つよそう。

この記事はクォータニオンを誰でも扱えるくらいになれることを目指した記事です。一方で、識者から見てもいい加減なことは書いてない記事を目指しています。

さっそく本題に入りましょう。

■とりあえずクォータニオンってなんだ

//　出たなクォータニオン
Quaternion qua = transform.rotation;

一言で説明すると、3次元上の向き（姿勢）を扱う時に便利なやつです。
もう少し詳細に説明すると、Vector3がオブジェクトの座標や、オブジェクトの移動に使えるものとするならば、Quaternionはオブジェクトの向き（姿勢）や、オブジェクトの回転に使えるものと表現する事ができます。使えるって言い方をしたのは、クォータニオン=「向き」そのものではないからです。もうちょっと下で説明します。

◆実はちゃんとした記事はある

実はクォータニオンをしっかり説明した記事が既にQiitaに存在します。

クォータニオン (Quaternion) を総整理！ ～ 三次元物体の回転と姿勢を鮮やかに扱う ～ - Qiita

クォータニオンを理解するうえでは完璧に網羅して説明している記事……なのですが、何分いくつか高度すぎる説明が多い。なんというか……数学専門の人が言う「簡単」「単純明快」ほど信用がおけない言葉ってないよね！！　（大暴言）

そんなわけで序文でも書いたように、この記事では本当の意味でわかりやすく、けれども専門の人から見てもいい加減ではないクォータニオンの説明を心掛けています。高校生以上で数学が致命的に苦手でないなら理解できるくらいの説明になっている……といいですね！

（一応言いますと、↑のQiitaの記事は本当に秀逸ではあるので、クォータニオンをしっかり理解したい人はマストで読むべき記事です。あるいはこの記事を読んで、もっと本格的に理解したい人が読んでもいいと思います）

◆オイラー角とは何が違うの？　オイラー角でよくね？

    // オイラー角はunity上ではVector3で制御するよ
    transform.eulerAngles = new Vector3(0, 0, 0);

    // rotationだとQuaternionで制御するよ
    transform.rotation = Quaternion.identity;

3次元上の向き……ていうとみんなも知ってるやつがいます。オイラー角と呼ばれる奴です。あいつとクォータニオンは何が違うのだろう？

オイラー角とは表現の仕方が違います。オイラー角は、X、Y、Zそれぞれの回転量をそのまま記述するため、直感的な分かりやすさではクォータニオンよりはるかに上を行きます。各成分を直接代入する時はオイラー角の方が安易であり、そのためUnity Editor上のTransformインスペクターのRotaionの項目も、オイラー角での入力が採用されています。

おなじみTranformインスペクタ

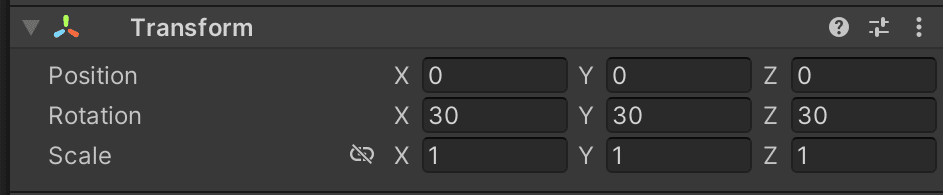
しかし、オイラー角は分かりやすさの反面、数学的な弱みをいくつか抱えています。具体的に言うと、オイラー角は回転量同士の加算や減算、補間などにあまり強くないです。こういった角度や回転にまつわる演算を行おうとした場合、クォータニオンの方に遥かに分があります。

2Dプラットフォームくらいならオイラー角で十分運用可能ですが、3Dの、それこそ飛行機がぶーんぶーんするフライトシミュレーションなどを想定すると、オイラー角での姿勢制御は難しくなります。ていうか修得さえすれば、どのケースであろうとクォータニオンはオイラー角より優れた制御力を発揮します。ゲームプログラマーなら修得をお勧めしたい内容です。

◆（補足）オイラー角の持つジンバルロック問題

これは実際に遭遇しないと少し体感し辛い問題なのですが、
オイラー角には「ジンバルロック」という有名な問題があります。

先述したように、オイラー角はX,Y,Zそれぞれの軸の回転量を入力する事で表現しますが、実際にはY軸、X軸、Z軸の順番に軸回転する事を示しています。さて、ここでX軸に90度を代入した場合……Y軸の回転とZ軸の回転が完全に一致してしまいます。これにより、意図した回転制御が行えなくなるリスクがあります。

Unityのジンバルロックを30秒で体感する - Qiita

こちらの記事に詳しく書いてあります。

■クォータニオンを一応ちゃんと理解する

この記事ではわかりやすく理解する事を遵守しつつも、「なんとなく角度を表すものらしい」ではなく、ちゃんとクォータニオンというのが何かというのも概念的に理解できる記事にしたいので。

◆クォータニオンの厳密な定義

クォータニオンとは、日本語で四元数の事を指します。

四元数 - Wikipedia

↑数学オタク以外には何を言っているのか分からないことに定評のある
wikipediaの数学系記事

厳密に数学的に解釈すると虚数単位うんにゃらが出てきますが、
我々ゲームプログラマー的に見れば、4つの数字で構成されるデータ、
位の認識で大丈夫だと思います。一般的には[ x , y , z , w ]で表されます。
3次元座標[ x , y , z ]にwが増えただけです。難しくない。

この四元数、クォータニオンは3次元上の向き・回転の計算を行う時に非常に都合がよい、らしいです（ふわふわ説明）。そのため、今のCGグラフィックス分野ではクォータニオンでの表現がスタンダードとなっています。

つまり、厳密にはクォータニオン=3次元上の向き・回転というわけではありません。が、Unityでのゲーム制作上でクォータニオンが出てきたときは、文脈的には99%3次元上での角度のやつ、と認識して問題ないと思います。
この記事でも以降はクォータニオン=3次元上での角度のやつと扱います。

◆クォータニオンはどうやって角度を表現している？

さて、クォータニオンが4つの成分[ x , y , z , w ]で表されるデータであること、そして3次元上の角度を表せるものであることはわかりましたが、
では実際はどういうふうに表現しているのか？

ざっくり説明すると、[ x , y , z ]の3成分で表現されるベクトルを軸にし、
w成分で表現される分回転する、となります。
つまり任意軸で任意分回転しますよ、という表現です。

ふわふわすぎるペイント図解

なんだ、簡単じゃないか。
[ 0 , 0 , 1 , 30 ]ならZ軸を軸に、30度回転するってわけだな！！

……というわけではないです。

概念的にはそれであっているのですが、数値がそのままダイレクトに
入るわけではありません。厳密な定義はこうなります。

正規化された軸ベクトルをλ[ x , y , z ]、回転量をΘとするときに、
以下の成分を持つ

// コードブロックの正しい使い方じゃねえ！
[ 
 x = λx * sin(Θ/2) , 
 y = λy * sin(Θ/2) , 
 z = λz * sin(Θ/2) , 
 w = cos(Θ/2) 
]
// （……noteでこういうの綺麗に記述できる文法あるん？）

なんでこういう値の持ち方をするかというと、
計算するときに都合がいいから、らしい です。らしい2回目。 

つまりZ軸を軸に30度回転するクォータニオン、は正しくはこうなります。

[ 0*sin(15°) , 0*sin(15°) , 1*sin(15°) , cos(15°) ] = [ 0 , 0 ,  0.258  ,  0.966 ]
 
数値だけ見るとなんのこっちゃって感じになります。しかし、実際にクォータニオンを運用する上で、この数値を意識する必要はほとんどありません。

◆こんなに「らしい」連発して大丈夫なんですか？

大丈夫です。unityでのゲーム制作上において、クォータニオンは結局、Quaternionクラスに定義されている各種メソッドで間接的に操作する事になるからです。クォータニオンの各成分の数値などを直接意識する必要性は皆無だし、クォータニオンの内部計算を具体的に知る必要もありません。

後述のメソッド一覧でも改めて紹介しますが、「クォータニオンは"任意軸"の"任意回転量"で表現できる」事をダイレクトに示すものとして、それらを相互に変換するためのAngleAxis関数とToAngleAxis関数がunity側で用意されています。

    // 任意回転量と任意軸からクォータニオンを生成できる
    Quaternion qua = Quaternion.AngleAxis(30, Vector3.forward);

    // 逆に任意のクォータニオンから回転軸と回転量を取得もできる
    float angle = 0.0f;
    Vector3 axis = Vector3.zero;
    qua.ToAngleAxis(out angle, out axis);

……こう書くと数学ガチ勢からは怒られそうだけど俺はしらん！

unity公式リファレンスでも成分直接触るなってお墨付きだからたぶん大丈夫！！！！

◆[没]　正規のクォータニオンや自由度の話

書こうかなとも思ったんですけど、どうあがいてもそれなりに専門的な話になるし、Unity上でクォータニオンを使えるようになるため上で全く不要の話になるので割愛します……

気になる人は「ノルムが1　自由度　クォータニオン　オイラー角」
あたりで調べてください。

クォータニオン (Quaternion) を総整理！ ～ 三次元物体の回転と姿勢を鮮やかに扱う ～ - Qiita

ていうかさっきもあげたこのQiita記事の最初の方に載ってる。

◆まとめ：結局Unityにおいてクォータニオンは何を表す？

一応定義からしっかり説明した（つもり）ですが、Unityでのゲーム制作上においては、この1点だけを理解すれば問題になることはまずないです。

・クォータニオン型は、任意軸の任意量の回転を表すデータ

では次に進みましょう。

■Unity上でのクォータニオンのつかいみち

ここから実際にUnityでゲームを作る上でのクォータニオンの具体例を記述していきます。すぐ上の項にも書いたように、Unity上でのクォータニオンは

オブジェクトの向き（姿勢）　ないしは回転量の情報を持つもの

と解釈すればおおよそ理解できると思います。

◆クォータニオンをオブジェクトの向きに設定

Quaternion qua = Quaternion.AngleAxis(30, Vector3.forward);
transform.rotation = qua;

GameObjectが持つtransform.rotationに代入する事ができます。
これはtransformインスペクタにあるRotationの項目に該当します。
（ただしインスペクタではオイラー角表記になることに注意してください）
（Quaternion.AngleAxisは後で説明します）

特にカメラのオブジェクトに代入する事が多いでしょうか。

◆オブジェクトの向きからクォータニオンを取得

Quaternion qua = transform.rotation;

もちろん逆にtranformから取得することもできます。

◆ベクトルに回転を適用

Vector3 v = new Vector3(1, 2, 3);
Quaternion qua = Quaternion.AngleAxis(30, Vector3.forward);
v = qua * v;

ベクトルに乗算する事で、クォータニオンの回転を適用する事ができます。
なお、Quaternion * Vector3の順序の演算のみ有効で、回転後のVector3を返します。Vector3 * Quaternionはコンパイルエラーとなります。

◆クォータニオンを組み合わせる

Quaternion qua1 = Quaternion.AngleAxis(30, Vector3.forward);
Quaternion qua2 = Quaternion.AngleAxis(30, Vector3.up);
Quaternion quafix = qua2 * qua1; 

クォータニオン同士を乗算する事ができます。
上の例では、quafixにはqua1の回転の後、qua2の回転を適用したものが入ります。右からであることに注意。筆者もよく間違えて逆に書く

他にもやれることはいくつかありますが、
基本的にはこの4つの運用法で殆どだと思います。

◆ていうかクォータニオンの演算って？

乗算する事で……と書きましたが、そもそもクォータニオンの四則演算はVector3に対する乗算と、クォータニオン同士の乗算しか実装されていません（Quaternionの定義をコードエディタで見ると分かります。あるいは公式ドキュメント）。それぞれどういう作用をするかは上記の項目の通りです。クォータニオン同士の乗算は、体感的には加算みたいな印象ですね。
（ただし「2つのクォータニオンをどっちの回転から適用するか」で
最終的な向きは変わります。つまり交換法則は成立しません）

■よく使うメソッド

使用例でも一部紹介しましたが、Quaternionクラスにはいくつものメソッドが用意されています。このおかげで、我々Unityゲームプログラマーはクォータニオンの数学的な理解をそこまでしなくとも、クォータニオンを扱えるわけです。まあDirectXでの回転行列もそんな感じだったけど

この項ではQuaternionクラスに生えてるメソッドのうち筆者がよく使うものを主観全開で紹介していきます。
※ぶっちゃけ「相互に片方のメソッドを使うならもうの片方メソッドは不要となる関係」みたいなものが結構あり、どのメソッドを愛用するかは結構個人差が出るのではないかと思ってます

◆Quaternion.AngleAxis　と　Quaternion.ToAngleAxis

Quaternion qua = Quaternion.AngleAxis(30, Vector3.forward);

前項でも紹介したAngleAxis君とToAngleAxis君です。
AngleAxisは軸と回転量を指定して、無からクォータニオンを生成するメソッドです。第一引数が回転量（度数法単位）、第二引数が回転軸です。上の例では、Z軸を軸に、時計回りに30度回転するクォータニオンを生成します。

無からクォータニオンを生成するメソッドでは最も使いやすい印象です。
筆者も一番使います。

float angle = 0.0f;
Vector3 axis = Vector3.zero;
transform.rotation.ToAngleAxis(out angle, out axis);

先程も説明しましたが、ToAngleAxisはAngleAxisの逆関数で、任意のクォータニオンを軸と回転量での表現に落とし込みます。自分はあまり使いませんが知っておくと便利なこともあるかも。

◆Quaternion.Identity

Quaternion qua = Quaternion.identity;

「回転しないクォータニオン」です。Vector3.zeroみたいなもの。
とりあえず初期化するときに代入しておくと便利です。
ちなみに内部的には[ 0 , 0 , 0 , 1 ]と扱われます。
sin(0)やcos(0)の値を考えれば自明ではある。

◆Quaternion.Slerp

Quaternion qua1 = Quaternion.AngleAxis(30, Vector3.forward);
Quaternion qua2 = Quaternion.AngleAxis(30, Vector3.up);
Quaternion quafix = Quaternion.Slerp(qua1, qua2, 0.5f);

2つのクォータニオンの補間値を出します。Vector3.Lerpに相当するメソッドです。クォータニオンがオイラー角と比べてめっちゃ強い点の1つです。
2つの角度を滑らかに補間する事が、クォータニオンとこのメソッドのお陰で容易に実現します。このメソッドの為だけでもクォータニオンに移行する価値はあります。

2つのクォータニオンの境界より先の値も取りたい場合は、SlerpUnclampedを使います。また、LerpメソッドもQuaternionクラスには生えていますが、これは2つのクォータニオンの単位点を結んだ線上の補間となり、一般的な角度の補間とは違うものです。こっちを使うケースはちょっと思い浮かびません。使うことは稀かと。

◆Random.rotation

Quaternion qua = Random.rotation;

これはQuaternionではなくRandomに生えているstaticプロパティです。ランダムな角度を得る事ができます。ちなみにパフォーマンスが多少落ちるものの、より精度を上げたい場合はRandom.rotationUniformを使うらしいです。どの程度精度が上がってどの程度パフォーマンスが落ちるかは知らない。

Quaternion quafix = Quaternion.Slerp(Quaternion.identity, Random.rotation, 0.25f);

先程説明したSlerpと合わせると、「範囲を狭めたランダム」なんかも
作る事ができます。ショットガンみたいなの作るときに便利。

個人的にオススメなのは以上のメソッドですが、他にも初学者にも使いやすいメソッドはあるのでいくつか説明しておきます。

◆Quaternion.LookRotation

Transform target=null; // 適当に見たい対象を入れてください
Quaternion qua = Quaternion.LookRotation((target.position - transform.position));

ベクトルからクォータニオンを生成します。メソッド名が示す通り、特定の座標から特定の座標を見るクォータニオンを産みだしたい時に使えます。特に、カメラの座標から特定のオブジェクトを注視したい、みたいなケースではとても役立つメソッドです。

ただ、注意点として、これで得られるクォータニオンは（そのままだと）空を上、地面を下としたものとなります。天地がひっくりかえっているクォータニオンにしたい場合、第二引数のupwardを指定する必要がありますが、そこを明示的に指定する必要があるケースでは既にこのメソッドは使い辛さの方が目立ち始めると思います。まあ天地がひっくり返らない一般的な3DプラットフォームやFPSなら十分使えます。

◆Quaternion.Euler & eulerAngles

一応オイラー角との相互変換は用意されています。便利なときもありますが、これで結局オイラー角でうんにゃらするのはクォータニオンを使うという観点では「んー？」てなるのであまり依存したくはないかも。

◆Quaternion.Inverse

逆方向の回転を得ます。w成分を逆にしただけとも言うが。
クォータニオンは*で足すことはできても、引く演算はありません。
クォータニオンを引く、は逆回転を足すことで行います。

一応紹介しましたが、ぶっちゃけこれを使うべきところで使える時点で十分な熟練者です。

◆メソッドまとめ

その他にもクォータニオン絡みのメソッドやプロパティはいくつか存在します。ぶっちゃけQuaternionクラスのメソッドはそんなに途方もない数あるわけではないです。なんとなく全部目を通す事ができるくらいの量です。慣れてきたら、一度全部目を通してみてもいいでしょう。

■クォータニオンのまとめ

以上。ここまで読めば、なんとなくクォータニオンを扱える気になってくるのではないでしょうか。いや、なれ（暗示）

クォータニオンを使いこなせばこーんなものも作れるようになります！！

カメラ傾けは演出に貢献するがユーザビリティを下げる諸刃の剣…… #unity3d #gamedev pic.twitter.com/tnIhPmYwns

— MetaFormer@Cubis(2/2)リリース (@MetaFormingPro) November 16, 2022

ステマじゃないかって？　そうですよ。

◆定型句

この記事がいいとおもったら
いいねとかシェアとかフォローとかお願いします！！
↑毎回コピペするときに奇妙な気持ちにはなる

◆謝辞

当記事はUGDGの皆さんの協力によって執筆されました。
この場を借りて感謝申し上げます。

↑UGDGについての記事はこちら。
UGDGよいとこいちどはおいで。