
BlenderのGeometryNodesで機械学習モデルを動かしてみた
機械学習モデル(ニューラルネットワーク)は、たくさんの数値に対して値をかけたり、足したり、合計したり…といった操作をすることで問題を解きます。
そしてGeometryNodesは、(本来は3Dモデリングやモーショングラフィックスのための機能ですが、)たくさんの頂点(ジオメトリ)に対して値をかけたり、足したり、合計したり…といった操作が可能です。
ということは機械学習モデルをGeometryNodesで動かすこともできそうですよね。
実際、動かせました。
すみません!本来出力にSoftMaxをかけるべきところを、いれていませんでした!
— Melville (@MelvilleTw) November 13, 2022
(出力の値は変わっていないのですが、可視化の印象がだいぶ変わります)
撮りなおしたので、最初の動画のことは忘れてこちらをご覧ください…!🙇 pic.twitter.com/fowj9Tm8lL
実際に動かしてみたい方は、
GitHubにBlendファイル等置いたのでそちらからどうぞ。
Blender 3.2以降推奨です。
機械学習モデルはpython等のライブラリを用いて動かすのが普通で、一見するとブラックボックスで敷居が高そう、と思われている方も多いと思いますが、基本的には中身の計算はただの掛け算や足し算ですので、うまくやればこういった芸当が可能なわけです。
これには一定の教育的価値があると思いますので、この記事を読んでいる方も真似て似たようなことができるよう、実装にあたって考えたことを書き留めておきます。

方針
まず、機械学習のHello Worldとも言えるMNIST手書き文字認識に目的を絞って考えていきます。
学習(トレーニング)自体をBlenderでやるのは流石に厳しいため、以下学習済みモデルをベースに作成していくことを考えます。
MNIST - Handwritten Digit Recognition (ONNX Model Zoo)
https://github.com/onnx/models/tree/main/vision/classification/mnist
ONNXファイル(学習済み機械学習モデルのファイル)をダウンロードし、Netron(ONNXファイル等の可視化ツール)で開くと、次のような構造になっていることがわかります。
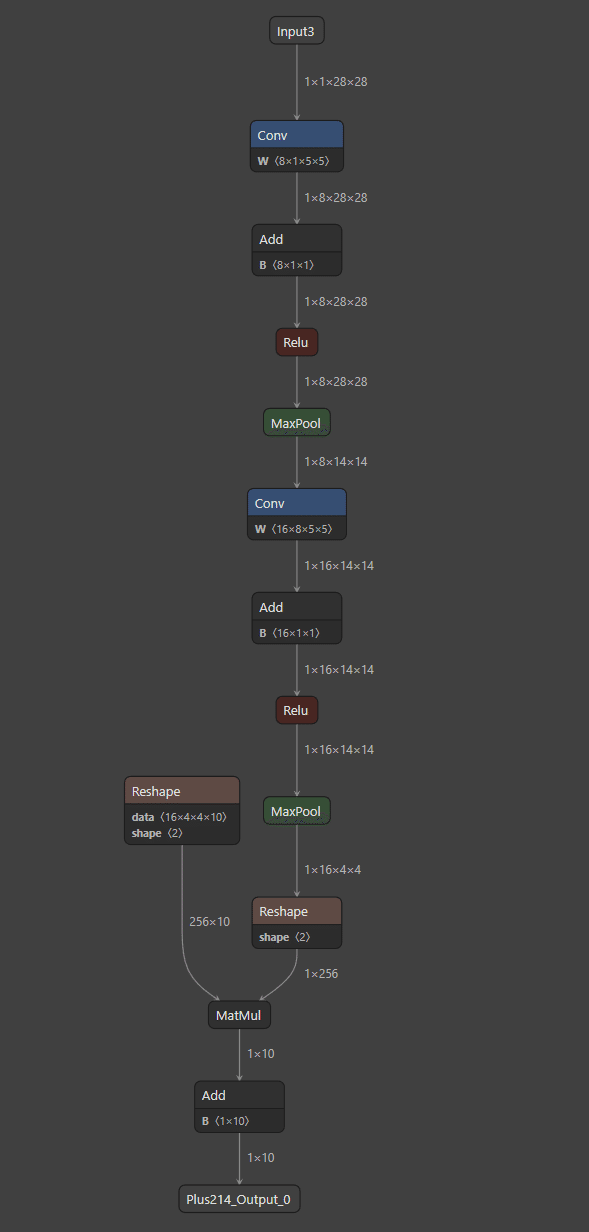
要するに、やるべきことは順に、
28x28ピクセルの画像を入力(Input)
重みパラメーターをかける(Conv)
バイアスパラメーターを足す(Add)
活性化関数を通す(ReLU)
2x2の最大値プーリングを行う(MaxPool)
重みパラメーターをかける(Conv)
バイアスパラメーターを足す(Add)
活性化関数を通す(ReLU)
3x3の最大値プーリングを行う(MaxPool)
行列に整形(Reshape)してパラメーターの行列とかける(MatMul)
バイアスパラメーターを足す(Add)
最終的に10個の数値として結果を得る(Output)
となります。
演算自体は基本的に足したりかけたりしているだけなので、とてもシンプルですが、問題は大量のパラメーターをどうやってGeometryNodesに持っていくかです。
結論から言うと、GeometryNodesでは画像テクスチャノードを用いると良く、これは任意の画像を読み込んで各ピクセルの値を取得する、といったことが可能です。
したがってパラメーターは画像化して各ピクセルの値を拾うことにします。
パラメーターの画像化
パラメーターはNetronで開いてノードプロパティを開くと、.npy形式で保存することが可能です。
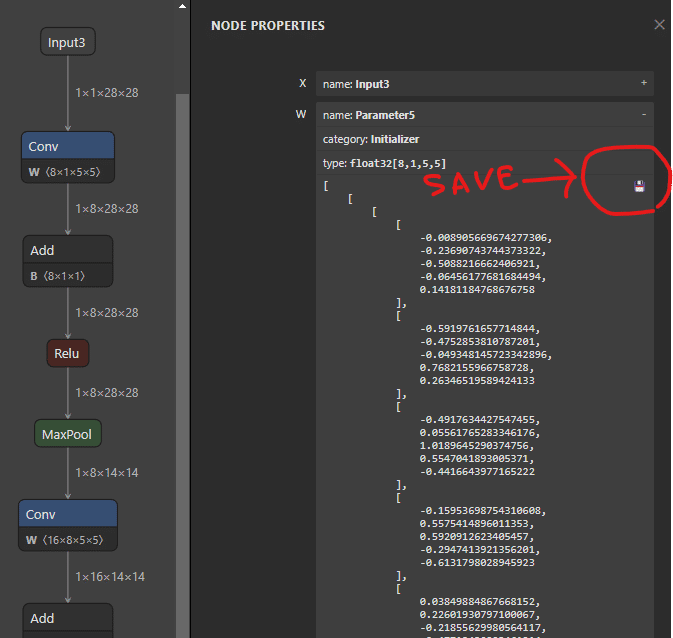
これであとはPillow等を用いて画像に変換すれば良いわけです。
(面倒な人は変換済みの画像も含め、GitHubにBlendファイルごと置いてありますのでそちらからどうぞ)
ただ「精度」と「座標系の違い」と「色空間」に注意する必要があります。
精度上の注意
元のONNXファイルに内包されているパラメーターは32bit浮動小数点数ですが、一般的な24bitのpng画像などを用いてグレースケールでパラメーターを表現しようとしたりすると8bitに情報量が落ちてしまいます。
が、この程度のニューラルネットワークであれば少しばかりパラメーターが変わってもそんなに大きく変化することはなく(事前に検証しました)、本質と関係ないところで話が複雑化するのも面倒です。
そのため特に工夫はせず、-1.0~1.0の数値がグレースケールの明度0~255に対応するよう変換することにしました。
座標系の違いの注意
画像ファイルでは通常左上が座標原点となりますが、
Blenderでは左下が座標原点です。
この差異はどこかで吸収する必要がありますが、私は適宜都合の良いように画像パラメーターの並びを変えることにしました。
色空間の注意
Blenderでは画像は読み込むとデフォルトで「sRGB」になっており、パラメーターとして読み込むには都合が良くないです。
各画像を画像エディターで開き「リニア」等に設定しておけば考えることが減ります。

入力(Input)

入力も画像テクスチャノードから明度情報を読み込みます。
Blenderには画像エディターがあるため、これを用いることで(上記ツイート動画でお見せしたように)リアルタイムに文字認識の検証を行うこともできます。
読み込んだ明度情報は正方形に並べた784(=28×28)個のポイントの半径として設定することで値を保持します。
畳み込み演算(Conv)

ここが今回の実装における肝と言って差し支えないのですが、隅々まで説明すると長くなってしまいますし、Blendファイルも配布しておりますので、ここでは掻い摘んで説明します。
フィールド蓄積ノードについて

BlenderのGeometryNodesにはフィールド蓄積ノードという非常に強力なノードがあります。
これはざっくり言うと点(ポイント)などがもつ情報(座標や半径やインデックスなど)それ自体や、そこから何かしらの計算を行った値の合計をとることが可能です。
合計といっても、ジオメトリの点に対して全ての合計だけでなく、任意にグループ分けしてそれぞれの合計を得ることもできます。
これは今回の用途に非常に都合が良い性質です。(どう用いるのかは後述)
ポイントの複製
今回のニューラルネットワークの1層目の畳み込み層では8種類の5x5フィルターを用いますので、200(=8×5×5)個のパラメーターがあります。
これらと、入力画像をフィルタをずらしながらかけて、合計をとる必要があります。
結論から言うと、まず入力画像を表すポイント数を200倍に増やし、適切に座標をずらし、同じ座標のポイント同士の合計をとれば良い、という状態にします。
この複製操作はポイントにインスタンス生成ノードを用いると可能です。

そして、同じ座標に属するポイント同士をグループとみなした上で先述のフィールド蓄積ノードを用いて合計を求め、これを新しいポイントの半径として設定すれば各ピクセルの畳み込み演算が可能、というわけです。
ポイントの半径の設定が終わり次第、200倍に増えてしまったポイントのうち不要なものは取り除いておきます。
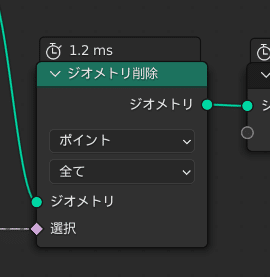
バイアス値の加算(Add)

こちらは畳み込み演算よりもシンプルで、単純に画像テクスチャから読んだ値を足すだけの処理となっています。
活性化関数(ReLU)

こちらは前述の操作よりも更にシンプルで、各ポイントについて現在の半径と0のうち大きい方を新しいポイントに設定することで活性化関数ReLUを実現しています。
最大値プーリング(MaxPool)

もっとシンプルになったのですが…)
最大値プーリングを行うためには当然値の比較を行い、ある範囲(例えば2×2領域)の最大値を取得する必要がありますが、残念ながらフィールド蓄積ノードは合計値しか求めることができず、最大値の取得はできません。
代わりにインデックスからフィールドノードをうまく用いることになります。

これは指定したインデックスのポイントなどがもつ情報(座標や半径やインデックスなど)それ自体や、そこから何かしらの計算を行った値の取得が可能です。
そして、あるポイントのインデックスに適当な値を足すことで、隣のポイントのインデックスを導くことが可能です。(例えば今回の場合、1を足すとひとつ右のポイントのインデックスに対応します)
やや面倒なのですが、以上を用いてインデックスをずらしたものを全て比較して得た最大値を新たにポイント半径に設定したうえで、不要なジオメトリを削除し、最大値プーリングが実現できます。
隙間が空いた分はトランスフォームノードを用いてジオメトリ全体のXとYのスケールを0.5倍することにより詰めることができます。

2層目も1層目と同様に
以上で畳み込み・プーリング層の1層目が完了です。
2層目も同様に畳み込み・プーリング層をつなげます。

全結合層(MatMul)

やるべきことは実質、より単純な畳み込み演算です。
出力(Output)

バイアスの加算と、ソフトマックスを通せば、10個のポイントの各半径が出力となります。🎉
結果の可視化
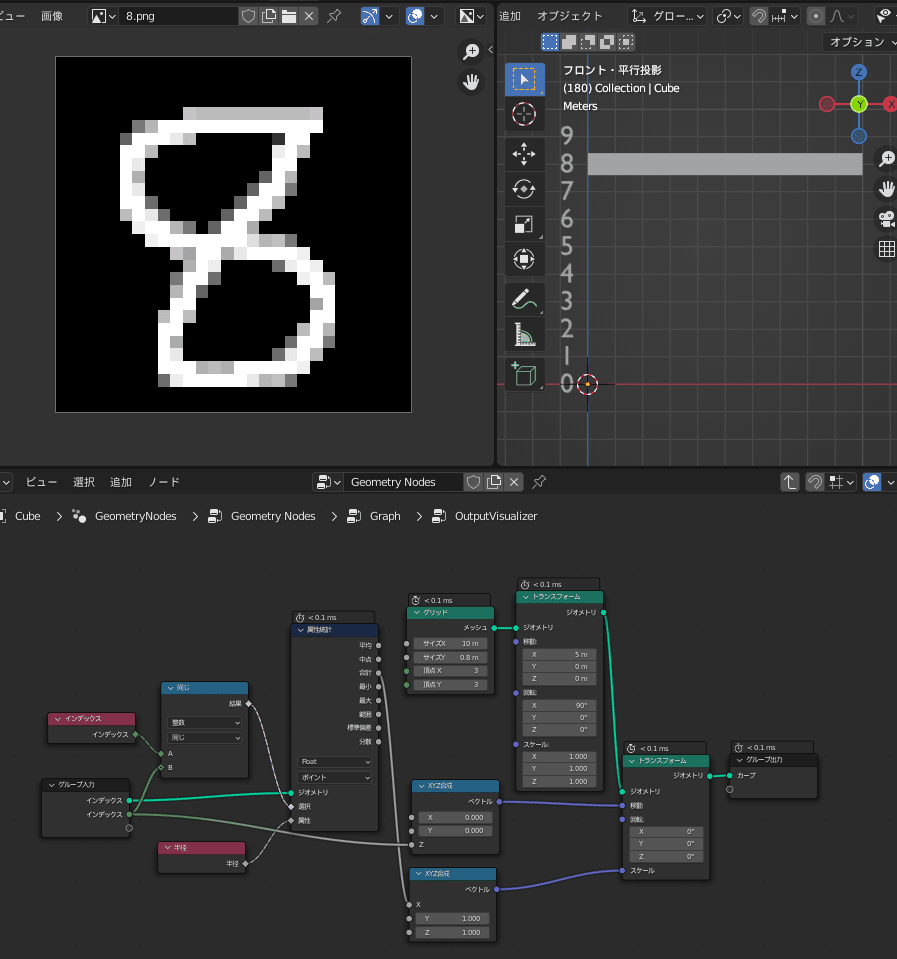
せっかく結果を得たのですから、何らかの可視化をしたいところです。
可視化にあたってはしばしばフィールドではなく単一の実数値(a single real value)が求められます。
これは上の図のように、特定のインデックスのポイントのみを指定した属性統計ノードを用いるなどで取得することができます。
上の図ではこのようにして得られた値を、四角いメッシュに対するX方向スケールとして用いることで棒グラフを表現しています。
おわりに
結構端折ってしまったのですが、以上となります。
GeometryNodesはできることが幅広く、ノードベースに組んだ計算結果がリアルタイムに反映されてくれるので嬉しいですね。
実際に機械学習モデルをライブラリなしで一から組み立てるというのは非常に勉強になりましたし、これが(適切な画像さえ事前に用意すれば)ノーコードで実装できるというのは教育的にも価値があるのではないかと思います。(逆に言うと教育的な価値しかないようにも思いますが…)
何度か記事中にもリンクを張りましたが、GitHubでBlendファイル等も公開しておりますので、手元で実際に動かしてみたいという方は是非どうぞ。
VMelville / mnist-geometrynodes
今回の話とはそんなに関係ないですが、他にもGeometryNodesで球面調和関数を描画したり、
行列計算を行わせて固有値問題を解いたり、
といった謎の取り組みも過去にやっておりますので、興味があれば是非こちらもご覧ください。
