
【高校数学】logを使って???小数の位を???
前回の続きです。
前回、対数の考え方を用いて莫大な数の概数を考えるという記事を書きました。
のですが、思ったより文章量が多くなってしまったので途中で挫折しました。すみません。
今回はその続きです。
復習の時間です
・底が10の対数っていうのは0が後ろに何個付くのかを表していました。
・だから対数取って常用対数表使って数値を出せば桁数が分かりました。
・とはいえ、2億と5億では3億の差があって、一番前の数が分からないと概数として役に立たないので、一番前の数を求める方法を考えました。
・えまって、これって小数にも応用できるんじゃね?
小数の桁数は??
てなわけで、桁数的なあれを小数の方にも応用してみます。
まぁ小数に桁は存在しないので、「小数点第何位か」という議論になりますが。
10の○○乗っていうのがどんどん減っていって、マイナス乗になったらどうなりますかね?
皆さん大好き小数になっていくんですね。

こんな感じで指数の数がそのまま小数第何位かを表してくれています。
とっても便利!!
そして何を隠そう、対数の値は0が何個続いてから数字が出てくるかを表していることになるのです。
10を底とする対数を取るとそうなることが分かりますね。
※しかし、ここでちょっと注意しなくちゃいけなくて、
+p乗の時と違って、純粋に「小数第p位に初めて0以外の数字が出てくる」としてはいけないことです。
ちょっと何言ってるかわからない(サンドウィッチマン
と思うので例を上げて説明します。
例えば、2の-1乗の場合、
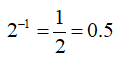
ですよね。
ですが、これの対数を取ってみると、
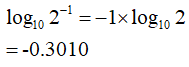
こうなります。
この時に、+p乗の時と同じ考え方でいると、
「-0.3010・・・初めて0でない数字が出てくるまでの0の数は0個・・・!
つまり、小数第0位が初めて0でない数字が出てくる場所だな!!?」
ってなってしまいます。あれ?本来、0.5って5が出てくるまでに0が1個ありますよね。
イメージ的には
「小数点より右側で0が何個出てくるかを表している」
となるのですが、
まぁそんなこと覚えづらいし、頭の中こんがらがるし、
「そういうもんなんだ」と思って、対数の結果の数字より1大きい数みたいに覚えておいた方が良いんじゃないでしょうか?
まとめると、
1.logを取る
2.常用対数表を使ってその数の概数を調べる
3.出てきた整数部分の絶対値に着目
4.その数よりも1大きい数が「0以外の数が初めて出てくるまでに出てきた0の数」
こんな感じでしょうか?
分かりづらいですね。
具体例を見てみましょう
具体例
例によって分かりやすい数字を使います。
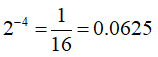
今回はこいつにお願いしましょう。
見ての通り、最初に0以外の数が出てくるのは小数第2位です。
じゃぁ実際に計算してみて、答えが一致するのか確認しましょう。
1.対数を取る
![]()
2.常用対数表で数値を調べる
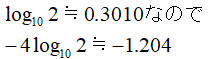
3.整数部分の絶対値を見る
整数部分は-1ですが、マイナスはおかしいので絶対値を見ます。
4.その数を1大きくする
今回は「1」だったので、それに1を足して「2」が答えになります。
はて、実際にどうかというと・・・
本当に小数第二位ですね!よくできています!!
まぢ感謝!親父お袋ありがとう!!!!
トップの数字を調べよう!
前回の記事では、莫大な数値の先頭の数字を調べようということをやりました。
とある指数の桁数が9桁だとわかって、
しかし、それだと2億かもしれないし、8億かもしれないです。
その差なんと6億!!!
こんなに精度の低い概数に何の意味があるんだ!!!!
ってなっちゃいますよね。
そこで、一番先頭の数字を考えてみるってことをしました。
もちろん、それを応用してやれば小数の先頭の数も分かります。
2億と8億だと6億も差があって、トップの数字が分かることのありがたみも伝わりますが、0.02と0.08だったら差は0.06でどっちにしても僅差です。
「こんなこと調べて何になるん?」って気になっちゃいますが、まぁそこは気にせずやってみましょう!
例は先ほどと同じ
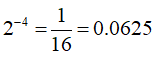
を使いましょう。
計算が正しければ、答えは「6」になるはずですよね!
まずはトップの数字を未知数にします。
まぁ今回もpとでもしておきましょうか。
これは小数第二位の数字だということが分かっているので、
![]()
と書き表すことができます。
即ち、
![]()
式で書くとこうです。
皆さんはもう、「指数が出てきたら対数を取れ」と洗脳されているはずなので、本能に従って対数を取ってみましょう。
![]()
logの中の掛け算は足し算にしてlogを分けましょう。
![]()
指数は下におろしましょう。
![]()
底と真数が同じだったら消えます。
![]()
log_10の2は大体0.3010くらいでした。
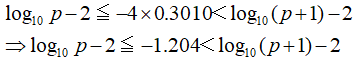
各辺に2を足しましょう。
![]()
ここまで来たら常用対数表を眺めながら0.796に近い数字を探します。

何となく一番0.7959が近そうですね。
その時のlogの値は6.25くらいらしいです。
pは自然数のはずなので、6.25の自然数部分だけ拾って「6」!
本当に答えが6になりました!!凄い!!便利!!!
おしまい
さぁみなさん、いかがだったでしょうか?
二記事にまたがってお送りした常用対数で桁数を求めよう編
対数の見方が変わったのではないでしょうか?
多分明日から皆さんがポケットに忍ばせるのはスマホから常用対数表に代わることと思います。
僕はスマホで常用対数表を調べますけどね!!!
ということで今回はここまで。
今回の記事がためになったという方、面白かったという方はぜひSNS等でシェアしてくださると嬉しいです。
また、「お疲れ!コーヒーでも飲みな!」という方はサポートをしてくださるととても励みになります!
また、他の記事もぜひ見てみて、ついでにTwitterのフォローもお願いします!!⇒https://twitter.com/mazenemaze
それでは、また次回の記事でお会いしましょう!!バイバイ!
