高校数学をプログラミングで解く（数学III編）「8-4 微分方程式」

割引あり

MK's papa

2025年1月15日 04:16

マガジンリスト　＞　数学Ⅲ編 8.積分法の応用　＞　8-4 微分方程式

はじめに

今回は、数学IIIで学ぶ「微分方程式」について、微分方程式の解を解析的に求めた場合とコンピュータで数値的に求めた場合とを図示して比較するプログラムを作成していきます。

微分方程式とその解

① 微分方程式　未知の関数の導関数を含む等式。例）

$$
\frac{dy}{dx}=x+1, \ \ \frac{dy}{dx}=y
$$

② 微分方程式の解　与えられた微分方程式を満たす関数。
微分方程式の解は、いくつかの任意の定数を含む関数となる。

微分方程式の解法

①

$$
\frac{dy}{dx}=f(x), \ \ \frac{d^2y}{dx^2} =g(x)
$$

などの解は、両辺を積分して求める。

②

$$
f(y) \frac{dy}{dx} = g(x)
$$

の解は

$$
\int f(y)dy = \int g(x) dx
$$

から求める。

③ $${x}$$と$${y}$$が混ざっているときは、分離して求める。例）

$$
\frac{dy}{dx} = x+xy \ \ \to \ \ y \neq -1 \mathrm{のとき} \frac{1}{1+y} \cdot \frac{dy}{dx} = x
$$

微分方程式の数値解法

微分方程式の解を数値的に求める方法の一つとして、記事『高校数学をプログラミングで解く（数学III編）「6-8 近似式」』で解説した（１次の）近似式を応用する方法が考えられます。つまり、関数$${f(x)}$$について、$${|h|}$$が十分小さいとき

$$
f(a+h) \fallingdotseq f(a)+f'(a) h
$$

と近似できることを利用します。

処理の流れ

微分方程式$${y' = f(x,y)}$$の解を$${y=F(x)}$$とします。この段階では、関数$${F(x)}$$は未知の関数です。この微分方程式の解$${y=F(x)}$$は点$${(x_0, y_0)}$$を通ることにします（つまり、$${y_0 = F(x_0)}$$）。

① $${\Delta x}$$を十分小さな値をもつ定数として

$$
x_k = x_0 + k \Delta x \ \ (k=0,1,2,\cdots,N)
$$

とします。これは公差$${\Delta x}$$の等差数列ですので、漸化式の形で

$$
x_{k+1} = x_k + \Delta x \ \ (k=0,1,2,\cdots,N-1)
$$

と書くこともできます。

② 次に、微分方程式の解が通る点$${(x_1,y_1)}$$を考えます。つまり、$${y_1 = F(x_1)}$$となる$${y_1}$$を考えます。$${F(x)}$$の形はわかりませんが、$${x_1=x_0+\Delta x}$$となることを利用して$${F(x_1)}$$を１次の近似式で表すと、

$$
y_1 = F(x_1) = F(x_0+\Delta x) \fallingdotseq F(x_0) + F'(x_0) \Delta x
$$

となり、$${y_0 = F(x_0)}$$、$${F'(x_0) = f(x_0, y_0)}$$となることを考慮すると、

$$
y_1 \fallingdotseq y_0 + f(x_0,y_0) \Delta x
$$

と表すことができます。つまり、$${y_0}$$や$${f(x_0,y_0)}$$の値はわかっているので、$${y_1}$$も近似的に求めることができます。この点$${(x_1,y_1)}$$を微分方程式の解が通る点とします。

③ 同様に、$${x_2 = x_1 + \Delta x}$$となることを利用して

$$
y_2 \fallingdotseq y_1 + f(x_1,y_1) \Delta x
$$

とし、$${x_3 = x_2 + \Delta x}$$となることを利用して

$$
y_3 \fallingdotseq y_2 + f(x_2,y_2) \Delta x
$$

というように、順に$${y_k \ \ (k=0,1,2,\cdots,N)}$$を求めていくと、点列$${(x_0,y_0),(x_1,y_1),(x_2,y_2), \cdots, (x_N, y_N)}$$を微分方程式の数値解とみなすことができ、これらの点を座標上で順に結んでいくことで微分方程式の数値解のグラフを描くことができます。

微分方程式の解析解と数値解の比較

今回は、微分方程式の解析解のグラフと数値解のグラフとをそれぞれ描いて比較するためのプログラムを作成します。

問題
次の微分方程式の解析解と数値解をもとめてそれらのグラフを描き、比較してみてください。ただし、微分方程式の解はいずれも原点を通ります。

$$
(1) \ \ \frac{dy}{dx} = x, \ \ \ \ (2) \ \ \frac{dy}{dx} = \cos x
$$

問題(1)の解析解

問題(1)の微分方程式は、微分方程式の解法①で解くことができ、一般解は、

$$
y = \frac{1}{2} x^2 + C \ \ ( C\mathrm{は積分定数} )
$$

と得られます。微分方程式の解は原点を通るので、解析解としては、

$$
y = \frac{1}{2} x^2
$$

となります。

問題(1)のプログラム

問題(1)の微分方程式の解析解のグラフと数値解のグラフとをそれぞれ描いて比較するためのプログラムを作成します。今回は、ベースとなるプログラムとして、記事『高校数学をプログラミングで解く（数学III編）「7-1 定積分とその基本性質」』で作成したスケッチ「compare_definite_integral」を再利用します。以下の zip ファイルをダウンロードして展開または解凍してください。

そして、スケッチの名前（フォルダ名）を「compare_derivative_equation1」と変更し、またスケッチ「compare_derivative_equation1」内の「compare_definite_integral.pde」ファイルの名前を「compare_derivative_equation1.pde」に変更します。そして、pdeファイル「compare_derivative_equation1.pde」をダブルクリックしてスケッチ「compare_derivative_equation1」の開発環境ウィンドウを立ち上げ、そのテキストエリアのソースコードを以下で書き換えます。

float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 10.0; // y軸の表示範囲 -y_rangeからy_rangeまで 

void setup(){
  size(500,500);
  noLoop();

  setAxes(x_range, y_range); // 座標軸の準備
  noFill();
  
  // 関数が通る点の座標
  float x0 = 0.0;
  float y0 = 0.0;
  
  // グラフの描画範囲  
  float x_min = x0;
  float x_max = x_range;
  
  // 微分方程式の解析解のグラフを描く
  stroke(0,255,0);  
  strokeWeight(5);
  draw_analytic_solution(x_min, x_max);

  // 微分方程式の数値解のグラフを描く
  stroke(255,0,0);
  strokeWeight(2);
  draw_numerical_solution(x0, y0);

}

// 導関数
float derivative(
  float x,
  float y
){
  return x;
}

// 微分方程式の解析解
float analytic_solution(
  float x
){
  return x*x/2.0;
}

// 微分方程式の解析解のグラフを描く関数
void draw_analytic_solution(
  float x_min, // グラフの定義域の下限
  float x_max  // グラフの定義域の上限
){
  int plot_num = 2000; // グラフを描くための頂点の個数  
  
  // グラフを描画
  float x, y; // 関数の座標
  float X, Y; // キャンバス上の座標 
  beginShape();
  for(int i=1; i<plot_num; i++){
    x = x_min + (x_max - x_min) / plot_num * i; // 曲線上の点のx座標
    y = analytic_solution(x); // 曲線上の点のyの値
    // キャンバス上の座標位置に換算
    X = width / 2.0 / x_range * x;
    Y = height / 2.0 / y_range * y;
    vertex(X, Y);
  }
  endShape();

}

// 微分方程式の数値解のグラフを描く関数
void draw_numerical_solution(
  float x0, // 関数が通る点のx座標
  float y0  // 関数が通る点のy座標
){
  float dx = 0.01; // 刻み幅
  int plot_num = int(x_range/dx); // グラフを描くための頂点の個数  
  
  // グラフを描画
  float x = x0; // グラフ上の点のx座標
  float y = y0; // グラフ上の点のy座標
  float X, Y; // キャンバス上の座標 
  beginShape();
  for(int i=0; i<plot_num; i++){
    // キャンバス上の座標位置に換算
    X = width / 2.0 / x_range * x;
    Y = height / 2.0 / y_range * y;
    vertex(X, Y);
    // 座標位置を更新
    y = y + derivative(x,y)*dx; // 関数上の点のy座標の更新
    x = x + dx; // 関数上の点のx座標の更新
  }
  endShape();

}

ソースコード1　問題(1)の微分方程式の解析解のグラフと数値解のグラフとをそれぞれ描いて比較するためのプログラム

ソースコード1では、微分方程式$${y'=f(x,y)}$$の$${f(x,y)}$$を derivative 関数として準備し、この関数を利用して、微分方程式の数値解法の節で説明した処理の流れに則って、微分方程式の数値解のグラフを描く関数 draw_numerical_solution を作成し、この関数を setup 関数内で呼び出すことで数値解のグラフを描いています。

ソースコード1を、スケッチ「compare_derivative_equation1」の「compare_derivative_equation1」タブのテキストエディタ部分に書いて実行すると、図1のように、実行ウィンドウのキャンバス上に問題(1)の微分方程式の解析解のグラフが緑色の太線で、数値解のグラフが赤色の線でそれぞれ描かれます。

問題(1)の微分方程式の解析解のグラフと数値解のグラフとが重なっており、微分方程式の数値解が正しく得られていることがわかります。

問題(2)の解析解

問題(2)の微分方程式も、微分方程式の解法①で解くことができ、一般解は、

$$
y = \sin x + C \ \ ( C\mathrm{は積分定数} )
$$

と得られます。微分方程式の解は原点を通るので、解析解としては、

$$
y = \sin x
$$

となります。

問題(2)のプログラム

先程作成したスケッチ「compare_derivative_equation1」を再利用します。スケッチ「compare_derivative_equation1」をフォルダごとコピーして、スケッチの名前（フォルダ名）を「compare_derivative_equation2」と変更し、またスケッチ「compare_derivative_equation2」内の「compare_derivative_equation1.pde」ファイルの名前を「compare_derivative_equation2.pde」に変更します。そして、pdeファイル「compare_derivative_equation2.pde」をダブルクリックしてスケッチ「compare_derivative_equation2」の開発環境ウィンドウを立ち上げ、そのテキストエリアのソースコードを以下で書き換えます。

float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 10.0; // y軸の表示範囲 -y_rangeからy_rangeまで 

void setup(){
  size(500,500);
  noLoop();

  setAxes(x_range, y_range); // 座標軸の準備
  noFill();
  
  // 関数が通る点の座標
  float x0 = 0.0;
  float y0 = 0.0;
  
  // グラフの描画範囲  
  float x_min = x0;
  float x_max = x_range;
  
  // 微分方程式の解析解のグラフを描く
  stroke(0,255,0);  
  strokeWeight(5);
  draw_analytic_solution(x_min, x_max);

  // 微分方程式の数値解のグラフを描く
  stroke(255,0,0);
  strokeWeight(2);
  draw_numerical_solution(x0, y0);

}

// 導関数
float derivative(
  float x,
  float y
){
  return cos(x);
}

// 微分方程式の解析解
float analytic_solution(
  float x
){
  return sin(x);
}

// 微分方程式の解析解のグラフを描く関数
void draw_analytic_solution(
  float x_min, // グラフの定義域の下限
  float x_max  // グラフの定義域の上限
){
  int plot_num = 2000; // グラフを描くための頂点の個数  
  
  // グラフを描画
  float x, y; // 関数の座標
  float X, Y; // キャンバス上の座標 
  beginShape();
  for(int i=1; i<plot_num; i++){
    x = x_min + (x_max - x_min) / plot_num * i; // 曲線上の点のx座標
    y = analytic_solution(x); // 曲線上の点のyの値
    // キャンバス上の座標位置に換算
    X = width / 2.0 / x_range * x;
    Y = height / 2.0 / y_range * y;
    vertex(X, Y);
  }
  endShape();

}

// 微分方程式の数値解のグラフを描く関数
void draw_numerical_solution(
  float x0, // 関数が通る点のx座標
  float y0  // 関数が通る点のy座標
){
  float dx = 0.01; // 刻み幅
  int plot_num = int(x_range/dx); // グラフを描くための頂点の個数  
  
  // グラフを描画
  float x = x0; // グラフ上の点のx座標
  float y = y0; // グラフ上の点のy座標
  float X, Y; // キャンバス上の座標 
  beginShape();
  for(int i=0; i<plot_num; i++){
    // キャンバス上の座標位置に換算
    X = width / 2.0 / x_range * x;
    Y = height / 2.0 / y_range * y;
    vertex(X, Y);
    // 座標位置を更新
    y = y + derivative(x,y)*dx; // 関数上の点のy座標の更新
    x = x + dx; // 関数上の点のx座標の更新
  }
  endShape();

}

ソースコード2　問題(2)の微分方程式の解析解のグラフと数値解のグラフとをそれぞれ描いて比較するためのプログラム

ソースコード2は、ソースコード1の導関数を与える関数 derivative を

// 導関数
float derivative(
  float x,
  float y
){
  return cos(x);
}

に、微分方程式の解析解を与える関数 analytic_solution を

// 微分方程式の解析解
float analytic_solution(
  float x
){
  return sin(x);
}

に、それぞれ書き換えたものになっています。

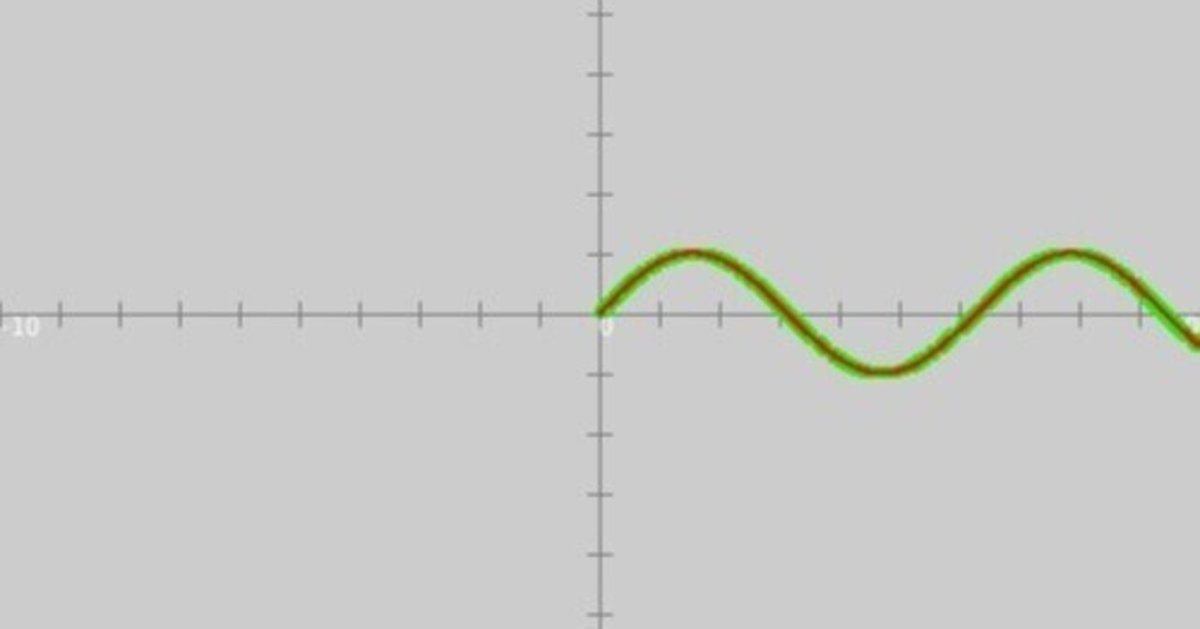
ソースコード2を、スケッチ「compare_derivative_equation2」の「compare_derivative_equation2」タブのテキストエディタ部分に書いて実行すると、図2のように、実行ウィンドウのキャンバス上に問題(2)の微分方程式の解析解のグラフが緑色の太線で、数値解のグラフが赤色の線でそれぞれ描かれます。

問題(2)の微分方程式の解析解のグラフと数値解のグラフとが重なっており、問題(2)の微分方程式の数値解も正しく得られていることがわかります。

まとめ

今回は、数学IIIで学ぶ「微分方程式」について、微分方程式の解を解析的に求めた場合とコンピュータで数値的に求めた場合とを図示して比較するプログラムを作成しました。
微分方程式の解をコンピュータで数値的に求める方法の一つとして、記事『高校数学をプログラミングで解く（数学III編）「6-8 近似式」』で解説した（１次の）近似式を応用する方法を利用しました。今回扱った問題では、解析解と比較して精度のよい数値解を求めることができました。
なお、今回は微分方程式の解が通る点$${(x_0,y_0)}$$を与えて、その点より右側（$${x}$$軸の正の向き）の領域での数値解を求めてグラフを描きましたが、点$${(x_0,y_0)}$$より左側（$${x}$$軸の負の向き）の領域でも、数値解を求めてグラフを描くことができます。例えば、微分方程式の数値解のグラフを描く関数 draw_numerical_solution 内の変数 dx の符号を反転させて

float dx = -0.01; // 刻み幅

とし、それに伴ってグラフを描くための頂点の個数を表す変数 plot_num を

int plot_num = int(x_range/abs(dx)); // グラフを描くための頂点の個数

と修正すると、点$${(x_0,y_0)}$$より左側（$${x}$$軸の負の向き）の領域のグラフを描くことができます。一度試してみてください。

読んだ感想などをお寄せください

本記事を読んだ感想や質問などを以下のお問い合せフォームからお寄せください。感想、質問をいただいた方には本記事の演習問題の解答をプレゼントします。（お問合せフォームの本文に、本記事のタイトルを入れてください。）

参考文献

改訂版教科書傍用スタンダード・オリジナル数学III（数研出版、ISBN9784410209567）

演習問題

次の微分方程式の解析解と数値解をもとめてそれらのグラフを描き、比較してみてください。ただし、微分方程式の解は原点を通ります。

$$
xy'+y=-y'+1
$$

演習問題の解答例

ここから先は

3,162字 / 1画像

期間限定！Amazon Payで支払うと抽選で
Amazonギフトカード5,000円分が当たる

ログイン

この記事が気に入ったらチップで応援してみませんか？