
高校数学をプログラミングで解く(数学B編)「4-5 確率変数の和と積」
マガジンリスト > 数学B編 4.確率分布と統計的な推測 > 4-5 確率変数の和と積
はじめに
今回は、数学Bで学ぶ「確率変数の和と積」について、確率変数$${X}$$と$${Y}$$の和に対する期待値、分散及び標準偏差を求めるプログラムを2つの方法を用いて作成します。
確率変数の和と積
まず、確率変換の和と積について解説しておきます。
確率変数の和と期待値
$${X,Y}$$は確率変数、$${a,b}$$は定数とする。
$${ E(X+Y)=E(X)+E(Y) }$$
$${ E(aX+bY)=aE(X)+bE(Y) }$$
確率変数の独立
2つの確率変数$${X,Y}$$があって、$${X}$$のとる任意の値$${a}$$と、$${Y}$$のとる任意の値$${b}$$について$${P(X=a, Y=b)=P(X=a)P(Y=b)}$$が成り立つとき、確率変数$${X}$$と$${Y}$$は互いに独立であるという。
独立な確率変数の積の期待値、和の分散
$${X,Y}$$は互いに独立な確率変数、$${a,b}$$は定数とする。
独立な確率変数の積の期待値
$${ E(XY) = E(X)E(Y) }$$
独立な確率変数の和の分散
$${V(X+Y)=V(X)+V(Y)}$$, $${V(aX+bY)=a^2V(X)+b^2V(Y)}$$
確率変数の和の期待値と標準偏差を計算する
今回は次のような問題を考えてみます。
問題
10円硬貨1枚と100円硬貨1枚を同時に投げるとき、表の出た硬貨の金額の和の期待値と標準偏差を求めよ。
なお、今回は、2つの方法で$${Y}$$の期待値と標準偏差を計算してみます。つまり、同時分布を利用して$${E(aX+bY), V(aX+bY)}$$で計算する方法と確率変数の独立性を利用して先に$${E(X),E(Y),V(X),V(Y)}$$を求めてその後$${aE(X)+bE(Y)}$$や$${a^2V(X)+b^2V(Y)}$$で計算する方法です。
アルゴリズム設計
今回は、$${X}$$を10円硬貨の裏が出たとき 0 、表が出たとき 1 となる確率変数とし、$${Y}$$を100円硬貨の裏が出たとき 0 、表が出たとき 1 となる確率変数とします。このとき、この問題の同時分布は
$$
\begin{array}{c||cc|c}
\hline
X \backslash Y & 0 & 1 & \mathrm{計} \\
\hline \hline
0 & 1/4 & 1/4 & 1/2 \\
1 & 1/4 & 1/4 & 1/2 \\
\hline
\mathrm{計} & 1/2 & 1/2 & 1 \\
\hline
\end{array}
$$
となります。1つ目のプログラムではこの同時分布を利用して、表の出た硬貨の金額の和の期待値$${m}$$と標準偏差$${\sigma}$$を計算します。
$$
m=E(10X+100Y) = \sum_{x=0}^1 \sum_{y=0}^1 (10x+100y)p_{x,y}
$$
$$
v = V(aX+bY) = \sum_{x=0}^1 \sum_{y=0}^1 (10x+100y -m)^2p_{x,y}
$$
$$
\sigma = \sqrt{v}
$$
もう一つのプログラムでは、確率変数$${X}$$と$${Y}$$の独立性を利用します。確率変数$${X}$$と$${Y}$$のそれぞれの確率分布は
$$
\begin{array}{c||cc|c}
\hline
X & 0 & 1 & \mathrm{計} \\
\hline \hline
P_{10} & 1/2 & 1/2 & 1 \\
\hline
\end{array}
$$
$$
\begin{array}{c||cc|c}
\hline
Y & 0 & 1 & \mathrm{計} \\
\hline \hline
P_{100} & 1/2 & 1/2 & 1 \\
\hline
\end{array}
$$
となります。これらの確率分布から確率変数$${X}$$の期待値$${m_X}$$と分散$${v_X}$$、確率変数$${Y}$$の期待値$${m_Y}$$と分散$${v_Y}$$は、それぞれ
$$
m_X = E(X) = \sum_{x=0}^1 x p_{10,x}, \ \ v_X = V(X) = \sum_{x=0}^1 (x -m_X)^2 p_{10,x}
$$
$$
m_Y = E(Y) = \sum_{y=0}^1 y p_{100,x}, \ \ v_Y = V(Y) = \sum_{y=0}^1 (y -m_Y)^2 p_{100,y}
$$
と計算することができます。これらの計算結果を利用して、表の出た硬貨の金額の和の期待値$${m}$$と標準偏差$${\sigma}$$は、
$$
m = 10 m_X + 100 m_Y
$$
$$
v = 10^2 v_X + 100^2 v_Y
$$
$$
\sigma = \sqrt{v}
$$
で計算することができます。
プログラム(同時分布を利用する)
では、$${X}$$と$${Y}$$の同時分布を利用して確率変数の和の期待値と標準偏差を計算するプログラムを作成していきます。
// 10円硬貨1枚と100円硬貨1枚を同時に投げるとき、
// 表の出た硬貨の金額の和の期待値と標準偏差を求める。
// 同時分布を利用
void setup(){
int a = 10; // 10円
int b = 100; // 100円
// 同時分布P
float[][] p = {{1.0/4.0,1.0/4.0},{1.0/4.0,1.0/4.0}};
// 同時分布による期待値の計算
float m = 0.0;
for(int x=0; x<=1; x++){ // 10円硬貨の裏(0)、表(1)
for(int y=0; y<=1; y++){ // 100円硬貨の裏(0)、表(1)
m = m + (a*x+b*y)*p[x][y];
}
}
// 同時分布による分散の計算
float v = 0;
for(int x=0; x<=1; x++){ // 10円硬貨の裏(0)、表(1)
for(int y=0; y<=1; y++){ // 100円硬貨の裏(0)、表(1)
v = v + (a*x+b*y-m)*(a*x+b*y-m)*p[x][y];
}
}
// 同時分布による標準偏差の計算
float sigma = sqrt(v);
// 期待値、分散、標準偏差の値をコンソールに出力
println("期待値 :", m);
println("分散 :", v);
println("標準偏差:", sigma);
}ソースコード1 同時分布を利用して計算するプログラム
このソースコードを、Processingの開発環境ウィンドウを開いて(スケッチ名を「SumofProbabilityVariables」としています)、テキストエディタ部分に書いて実行します。
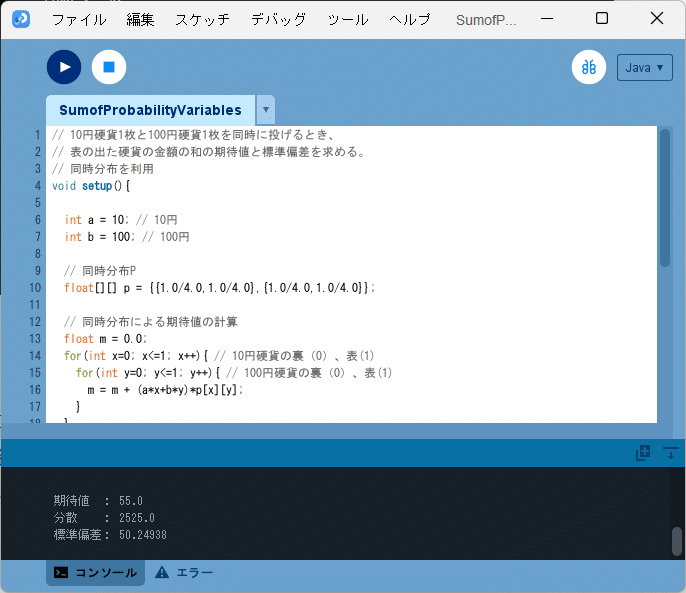
図1のように、確率変数の和の期待値、分散と標準偏差が
期待値 : 55.0
分散 : 2525.0
標準偏差: 50.24938
とコンソールに出力されます。なお、標準偏差の値は$${5 \sqrt{101}}$$となっています。
プログラム(確率変数の独立性を利用する)
次に、確率変数$${X}$$と$${Y}$$の独立性を利用して確率変数の和の期待値と標準偏差を計算するプログラムを作成していきます。
// 10円硬貨1枚と100円硬貨1枚を同時に投げるとき、
// 表の出た硬貨の金額の和の期待値と標準偏差を求める。
// 確率変数の独立性を利用
void setup(){
int a = 10; // 10円
int b = 100; // 100円
// 10円硬貨の裏表が出る確率分布
float[] p_ten = {1.0/2.0,1.0/2.0};
// 100円硬貨の裏表が出る確率分布
float[] p_hundred = {1.0/2.0,1.0/2.0};
// 独立な確率変数による期待値の計算
float m_ten = 0.0; // 10円玉の期待値
for(int x=0; x<=1; x++){ // 10円硬貨の裏(0)、表(1)
m_ten = m_ten + x*p_ten[x];
}
float m_hundred = 0.0; // 100円玉の期待値
for(int y=0; y<=1; y++){ // 100円硬貨の裏(0)、表(1)
m_hundred = m_hundred + y*p_hundred[y];
}
float m = a * m_ten + b * m_hundred ;
// 独立な確率変数による分散の計算
float v_ten = 0.0; // 10円玉の分散
for(int x=0; x<=1; x++){ // 10円硬貨の裏(0)、表(1)
v_ten = v_ten + (x-m_ten)*(x-m_ten)*p_ten[x];
}
float v_hundred = 0.0; // 100円玉の分散
for(int y=0; y<=1; y++){ // 100円硬貨の裏(0)、表(1)
v_hundred = v_hundred + (y-m_hundred)*(y-m_hundred)*p_hundred[y];
}
float v = a * a * v_ten + b * b * v_hundred;
// 標準偏差の計算
float sigma = sqrt(v);
// 期待値、分散、標準偏差の値をコンソールに出力
println("期待値 :", m);
println("分散 :", v);
println("標準偏差:", sigma);
}ソースコード2 確率変数の独立性を利用して計算するプログラム
このソースコードを、Processingの開発環境ウィンドウを開いて(スケッチ名を「SumofProbabilityVariables2」としています)、テキストエディタ部分に書いて実行します。

図2のように、確率変数の和の期待値、分散と標準偏差が
期待値 : 55.0
分散 : 2525.0
標準偏差: 50.24938
とコンソールに出力されます。これらの値は、同時分布を利用した場合(図1)と一致していることがわかります。
まとめ
今回は、数学Bで学ぶ「確率変数の和と積」について、確率変数$${X}$$と$${Y}$$の和に対する期待値、分散及び標準偏差を求めるプログラムを2つの方法を用いて作成しました。
1つ目のプログラムは確率変数$${X}$$と$${Y}$$の同時分布を用いて確率変数の和$${aX+bY}$$の期待値、分散及び標準偏差を計算するプログラムを作成しました。これらの結果は、最初の「確率変数の和と積」の節で紹介した確率変数の和の期待値の式
$$
E(aX+bY)=aE(X)+bE(Y)
$$
や、分散の式
$$
V(aX+bY)=a^2V(X)+b^2V(Y)
$$
の左辺を計算したことになります。
一方、2つ目のプログラムは確率変数$${X}$$と$${Y}$$についてそれぞれ期待値と分散を求めてから確率変数$${X}$$と$${Y}$$が独立であることを用いて、確率変数の和の期待値、分散及び標準偏差を計算するプログラムを作成しました。これらの結果は、確率変数の和の期待値や分散の式の右辺を計算したことになります。
2つのプログラムで計算した確率変数の和の期待値、分散及び標準偏差はそれぞれ一致しました。つまり、今回2つの方法で行った結果により、上記の確率変数の和の期待値や分散の関係式が成り立っていることを確認することができたわけです。
ただ、これらの結果は関係式が成り立っていることを証明したわけではないことに注意してください。証明は、確率変数$${X}$$と$${Y}$$が独立であることを表す確率分布の式
$$
P(X=a, Y=b)=P(X=a)P(Y=b)
$$
を利用すると比較的簡単にできますので、一度計算しておくことをお勧めします。
参考文献
改訂版 教科書傍用 スタンダード 数学B(数研出版、ISBN9784410209468)
