高校数学をプログラミングで解く（数学III編）「2-3 双曲線」

マガジンリスト　＞　数学Ⅲ編 2.式と曲線　＞　2-3 双曲線

はじめに

今回は、数学IIIで学ぶ「双曲線」について、双曲線を描くプログラムを作成します。

双曲線

まず、双曲線について解説します。

定義

異なる２定点$${\mathrm{F}}$$、$${\mathrm{F}'}$$までの距離の差が一定である点$${\mathrm{P}}$$の軌跡を 双曲線 といい，２定点$${\mathrm{F}}$$、$${\mathrm{F}'}$$をその 焦点 という。

焦点がx軸上にある双曲線

$$
\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \ \ (a > 0,  b > 0)
$$

[1] 中心は原点、頂点は２点$${(a,0), (-a,0)}$$
[2] 焦点は２点$${(\sqrt{a^2+b^2},0), \ \ (-\sqrt{a^2+b^2},0)}$$
[3] 双曲線は$${x}$$軸、$${y}$$軸、原点に関して対称である。
[4] 漸近線は２直線$${ \frac{x}{a}-\frac{y}{b}=0,  \frac{x}{a}+\frac{y}{b}=0}$$
[5] 双曲線上の点から２つの焦点までの距離の差は $${2a}$$

図1　焦点がx軸上にある双曲線

焦点がy軸上にある双曲線

$$
\frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 \ \ (a > 0, b>0)
$$

[1] 中心は原点、頂点は２点$${(0,b), (0,-b)}$$
[2] 焦点は２点$${(0,\sqrt{a^2+b^2}), \ \ (0,-\sqrt{a^2+b^2})}$$
[3] 双曲線は$${x}$$軸、$${y}$$軸、原点に関して対称である。
[4] 漸近線は２直線$${ \frac{x}{a}-\frac{y}{b}=0,  \frac{x}{a}+\frac{y}{b}=0}$$
[5] 双曲線上の点から２つの焦点までの距離の差は $${2b}$$

図2　焦点がy軸上にある双曲線

双曲線を描く

では、双曲線を描くプログラムを作成していきます。

問題1
次のような双曲線の方程式を求め、座標上に描け。
(1) 双曲線上の点と２つの焦点$${(6,0), (-6,0)}$$までの距離の差が$${6}$$
(2) 焦点が$${(0,3), (0,-3)}$$で、点$${(4,5)}$$を通る
(3) 漸近線が２直線$${y=2x, y=-2x}$$で、点$${(3,0)}$$を通る
(4) 漸近線が直交して、焦点が$${(3,0), (-3,0)}$$である

アルゴリズム設計

まず、今回の問題1に対する双曲線の方程式を求めてみます。基本的には、焦点の位置や漸近線の位置から、方程式は

$$
\frac{x^2}{a^2} - \frac{y^2}{b^2} = \pm 1 \ \ (a > 0,  b > 0)
$$

の形になります。
(1)は、その条件から、

$$
\sqrt{a^2+b^2} = 6, \ \ 2a = 6
$$

となるので、$${a=3,b=3\sqrt{3}}$$となり、方程式は、

$$
\frac{x^2}{9} - \frac{y^2}{27} = 1
$$

となります。
(2)は、

$$
\sqrt{a^2+b^2} = 3, \ \ \frac{16}{a^2}-\frac{25}{b^2} = -1
$$

となるので、$${a=2,b=\sqrt{5}}$$となり、方程式は、

$$
\frac{x^2}{4} - \frac{y^2}{5} = -1
$$

となります。
(3)は、漸近線が

$$
x-\frac{y}{2} = 0, \ \ x+\frac{y}{2} = 0
$$

となるので、$${b=2a}$$となります。また、双曲線が点$${(3,0)}$$を通ることから、

$$
\frac{9}{a^2}=1
$$

となるので、$${a=3, b=6}$$となり、方程式は

$$
\frac{x^2}{3^2} - \frac{y^2}{6^2} = 1
$$

となります。
(4)は、漸近線が直交することから

$$
\frac{b}{a} \cdot \left( -\frac{b}{a} \right) = -1
$$

となり、また、焦点が$${(3,0), (-3,0)}$$であることから、

$$
\sqrt{a^2+b^2}=3
$$

となるので、$${a=\frac{3\sqrt{2}}{2}, b=\frac{3\sqrt{2}}{2}}$$となり、方程式は

$$
\frac{2x^2}{9} - \frac{2y^2}{9} = 1
$$

となります。

プログラム

では、焦点が$${x}$$軸上または$${y}$$軸上にある双曲線を描くプログラムを作成していきます。ここでは、問題1(1)を例として作成しています。
グラフを描くので、記事『高校数学をプログラミングで解く（数学I編）「1-0-2 グラフを描くための準備（その2）」』で準備した座標軸を描く関数 setAxes を利用します。以下の zip ファイルをダウンロードして展開または解凍してください。

drawFunction.zip

1.38 KB

ファイルダウンロードについて

ダウンロード

そして、スケッチの名前（フォルダ名）を「draw_hyperbola」と変更し、またスケッチ「draw_hyperbola」内の「drawFunction.pde」ファイルの名前を「draw_hyperbola.pde」に変更します。そして、pdeファイル「draw_hyperbola.pde」をダブルクリックしてスケッチ「draw_hyperbola」の開発環境ウィンドウを立ち上げます。そして、開発環境ウィンドウのタブ欄で「draw_hyperbola」タブを選択して、そのテキストエリアのソースコードを以下のソースコード1に書き換えます。

float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 10.0; // y軸の表示範囲 -y_rangeからy_rangeまで 

void setup(){
  size(500,500);
  noLoop();

  setAxes(x_range, y_range); // 座標軸の準備
  
  noFill();
  stroke(0,0,0);

  float a,b; // 双曲線の係数
  stroke(255,0,0);
  // (1) 
  a = 3.0;
  b = 3.0 * sqrt(3.0);
  draw_hyperbola_x_axis(a,b);

}

// 焦点がx軸上にある双曲線を描く関数
void draw_hyperbola_x_axis(
  float a, // x^2の係数
  float b  // y^2の係数
){
  // グラフの定義域
  float y_min = -y_range;
  float y_max = y_range;
  int plot_num = 200; // グラフを描くための頂点の個数  
  
  // グラフを描画
  float x, y; // 関数の座標
  float X, Y; // キャンバス上の座標 
  // x>0の双曲線
  beginShape();
  for(int i=0; i<=plot_num; i++){
    y = y_min + (y_max - y_min) / plot_num * i; // 双曲線上の点のy座標
    x = a * sqrt(y*y/b/b+1.0); // 双曲線上の点のx座標
    // キャンバス上の座標位置に換算
    X = width / 2.0 / x_range * x;
    Y = height / 2.0 / y_range * y;
    vertex(X, Y);
  }
  endShape();
  // x<0の双曲線
  beginShape();
  for(int i=0; i<=plot_num; i++){
    y = y_min + (y_max - y_min) / plot_num * i; // 双曲線上の点のy座標
    x = -a * sqrt(y*y/b/b+1.0); // 双曲線上の点のx座標
    // キャンバス上の座標位置に換算
    X = width / 2.0 / x_range * x;
    Y = height / 2.0 / y_range * y;
    vertex(X, Y);
  }
  endShape();

  // 焦点をプロット
  x = sqrt(a*a+b*b);
  y = 0.0;
  plot_point(x,y);
  plot_point(-x,y);
  
  // 漸近線を描く
  x = x_range;
  y = b * x / a;
  X = width / 2.0 / x_range * x;
  Y = height / 2.0 / y_range * y;
  line(-X, -Y, X, Y);
  line(-X, Y, X, -Y);
}  

// 焦点がy軸上にある双曲線を描く関数
void draw_hyperbola_y_axis(
  float a, // x^2の係数
  float b  // y^2の係数
){
  // グラフの定義域
  float x_min = -x_range;
  float x_max = x_range;
  int plot_num = 200; // グラフを描くための頂点の個数  
  
  // グラフを描画
  float x, y; // 関数の座標
  float X, Y; // キャンバス上の座標
  // y>0の双曲線
  beginShape();
  for(int i=0; i<=plot_num; i++){
    x = x_min + (x_max - x_min) / plot_num * i; // 双曲線上の点のx座標
    y = b * sqrt(x*x/a/a+1.0); // 双曲線上の点のy座標
    // キャンバス上の座標位置に換算
    X = width / 2.0 / x_range * x;
    Y = height / 2.0 / y_range * y;
    vertex(X, Y);
  }
  endShape();
  // y<0の双曲線
  beginShape();
  for(int i=0; i<=plot_num; i++){
    x = x_min + (x_max - x_min) / plot_num * i; // 双曲線上の点のx座標
    y = -b * sqrt(x*x/a/a+1.0); // 双曲線上の点のy座標
    // キャンバス上の座標位置に換算
    X = width / 2.0 / x_range * x;
    Y = height / 2.0 / y_range * y;
    vertex(X, Y);
  }
  endShape();

  // 焦点をプロット
  x = 0.0;
  y = sqrt(a*a+b*b);
  plot_point(x,y);
  plot_point(x,-y);
  
  // 漸近線を描く
  x = x_range;
  y = b * x / a;
  X = width / 2.0 / x_range * x;
  Y = height / 2.0 / y_range * y;
  line(-X, -Y, X, Y);
  line(-X, Y, X, -Y);
  
}

// 座標(x,y)に点をプロットする関数
void plot_point(
  float x, // 点のx座標
  float y  // 点のy座標
){
  float X, Y; // キャンバス上の座標
  // キャンバス上の座標位置に換算
  X = width / 2.0 / x_range * x;
  Y = height / 2.0 / y_range * y;
  strokeWeight(5);
  point(X, Y);
  strokeWeight(1);
}

ソースコード1　焦点が$${x}$$軸上または$${y}$$軸上にある双曲線を描くプログラム

ソースコード1では、焦点が$${x}$$軸上にある双曲線を描く関数 draw_hyperbola_x_axis と焦点が$${y}$$軸上にある双曲線を描く関数 draw_hyperbola_y_axis の２つの関数を準備して利用しました。また、それぞれの関数は双曲線の焦点と漸近線を描くようにしています。

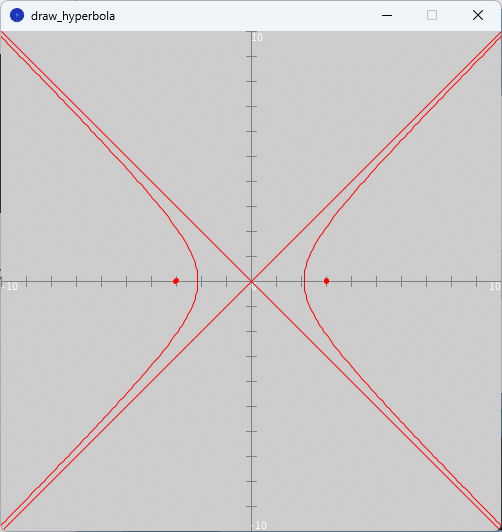
「draw_hyperbola」タブのテキストエリアをソースコード1に書き換えて、スケッチ「draw_hyperbola」を実行すると、図3のように、実行ウィンドウのキャンバス上に問題1(1)の双曲線が赤色で描かれます。

図3　問題1(1)の双曲線

問題1(2)の双曲線
次に、問題1(2)の双曲線を描きます。これには、ソースコード1の

  // (1) 
  a = 3.0;
  b = 3.0 * sqrt(3.0);
  draw_hyperbola_x_axis(a,b);

の部分を

  // (2)
  a = 2.0;
  b = sqrt(5.0);
  draw_hyperbola_y_axis(a,b);

に書き換えて、スケッチ「draw_hyperbola」を実行することで実現できます（図4）。なお、問題1(2)の双曲線は焦点が$${y}$$軸上にあるので、draw_hyperbola_y_axis 関数を利用します。

図4　問題1(2)の双曲線

問題1(3)の双曲線
ソースコード1の

  // (1) 
  a = 3.0;
  b = 3.0 * sqrt(3.0);
  draw_hyperbola_x_axis(a,b);

の部分を

  // (3) 
  a = 3.0;
  b = 6.0;
  draw_hyperbola_x_axis(a,b);

に書き換えて、スケッチ「draw_hyperbola」を実行すると、問題1(3)の双曲線を描くことができます（図5）。

図5　問題1(3)の双曲線

問題1(4)の双曲線
ソースコード1の

  // (1) 
  a = 3.0;
  b = 3.0 * sqrt(3.0);
  draw_hyperbola_x_axis(a,b);

の部分を

  // (4) 
  a = 3.0/sqrt(2.0);
  b = 3.0/sqrt(2.0);
  draw_hyperbola_x_axis(a,b);

に書き換えて、スケッチ「draw_hyperbola」を実行すると、問題1(4)の双曲線を描くことができます（図6）。

図6　問題1(4)の双曲線

一般的な双曲線の軌跡を描く

上記の問題1では、焦点が$${x}$$軸上または$${y}$$軸上にある双曲線を扱いましたが、今度は、より一般的な双曲線の軌跡を考えてみます。つまり、異なる２定点（焦点）$${\mathrm{F}(a_1, b_1)}$$、$${\mathrm{F}'(a_2,b_2)}$$までの距離の差が$${r}$$となる点$${\mathrm{P}(x,y)}$$の軌跡を考えます。

問題2
2定点$${(4,1), (-3,-2)}$$までの距離の差が$${5}$$となる点$${\mathrm{P}(x,y)}$$の軌跡を描け。

アルゴリズム設計

この一般的な双曲線の軌跡を描くにあたり、記事『高校数学をプログラミングで解く（数学II編）「2-5 軌跡と方程式」』で解説した方法を利用します。
つまり、$${xy}$$平面の描画範囲内の任意の点$${(x,y)}$$を取ってきて、その点と２定点との距離の差が$${r}$$になっているかどうかを確かめ、$${r}$$になっていればその点をキャンバス上の$${xy}$$平面にプロットし、$${r}$$になっていなければプロットしないというルールで行います。そして、プロットされた点が描く軌跡が双曲線になっているかを確認します。なお、記事『高校数学をプログラミングで解く（数学III編）「1-4 複素数と図形（１）」』で作成したスケッチ「drawTrajectory_complex」でも同様の方法を利用しているので、そちらの解説も確認してみてください。

プログラム

先程作成したスケッチ「draw_hyperbola」を再利用します。
スケッチ「draw_hyperbola」をフォルダごとコピーして、スケッチの名前（フォルダ名）を「draw_hyperbola_general」と変更し、またスケッチ「draw_hyperbola_general」内の「draw_hyperbola.pde」ファイルの名前を「draw_hyperbola_general.pde」に変更します。そして、pdeファイル「draw_hyperbola_general.pde」をダブルクリックしてスケッチ「draw_hyperbola_general」の開発環境ウィンドウを立ち上げます。

問題2の一般的な双曲線の軌跡を描くプログラムを作成していきます。

// 双曲線の定義を満たす点が描く図形
float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 10.0; // y軸の表示範囲 -y_rangeからy_rangeまで 

void setup(){
  size(500,500,P2D); // widthとheightは同じにしておく
  noLoop();

  setAxes(x_range, y_range); // 座標軸の準備
  
  noFill(); // グラフの中身を塗りつぶさない
  stroke(0,0,0); // グラフの線の色を黒色に設定
  
  // 点の生成回数
  int n = 1000000;
  // マージン
  float e = 0.001;
 
  // １つ目の焦点の座標
  float a1 = 4.0;
  float b1 = 1.0;
  
  // ２つ目の焦点の座標
  float a2 = -3.0;
  float b2 = -2.0;
  
  // 距離の差
  float r = 5.0;
  
  float x, y; // 任意の点の座標
  float l1; // １つ目の焦点との距離
  float l2; // ２つ目の焦点との距離
  for(int i=0; i<n; i++){
    // 任意の複素数を生成
    x = random(-x_range, x_range);
    y = random(-y_range, y_range);
    
    // ２つの焦点との距離の和がrになればプロット
    stroke(255,0,0);
    l1 = sqrt((x-a1)*(x-a1)+(y-b1)*(y-b1));
    l2 = sqrt((x-a2)*(x-a2)+(y-b2)*(y-b2));
    if( abs(abs(l1-l2)-r) < e ){
      plot_point(x,y);
    }    
  }
  
  // 焦点をプロット
  stroke(0,0,255);
  plot_point(a1,b1);
  plot_point(a2,b2);
  
}

// 座標(x,y)に点をプロットする関数
void plot_point(
  float x, // 点のx座標
  float y  // 点のy座標
){
  float X, Y; // キャンバス上の座標
  // キャンバス上の座標位置に換算
  X = width / 2.0 / x_range * x;
  Y = height / 2.0 / y_range * y;
  strokeWeight(5);
  point(X, Y);
  strokeWeight(1);
}

ソースコード2　一般的な双曲線の軌跡を描くプログラム

スケッチ「draw_hyperbola_general」の「draw_hyperbola_general」タブを選択してそのテキストエディタ部分をソースコード2で書き換えて実行すると、図7のように、実行ウィンドウのキャンバスの$${xy}$$平面上に、問題2の双曲線の軌跡が赤色、双曲線の２つの焦点が青色で描かれます。

図7　一般的な双曲線の描画

まとめ

今回は、数学IIIで学ぶ「双曲線」について、双曲線を描くプログラムを２つ作成しました。
１つ目は、原点を中心とし、焦点が$${x}$$軸上または$${y}$$軸上にある双曲線を描くプログラムを作成しました。プログラムでは、焦点が$${x}$$軸上にある双曲線を描く関数 draw_hyperbola_x_axis と焦点が$${x}$$軸上にある双曲線を描く関数 draw_hyperbola_y_axis との２つの関数を準備して利用しました。
２つ目は、双曲線の定義「異なる２定点（焦点）$${\mathrm{F}}$$、$${\mathrm{F}'}$$までの距離の差が$${r}$$となる点$${\mathrm{P}}$$の軌跡」に基づいて一般的な双曲線の軌跡を描くプログラムを作成しました。こちらについては、$${xy}$$平面上の任意の点を取ってきて定義を満たせば、$${xy}$$平面上にプロットするという方法を取りました。
定義に基づいた一般的な双曲線は、原点を中心とし、焦点が$${x}$$軸上または$${y}$$軸上にある双曲線を平行移動や回転したものになっています。これについては別の記事で紹介します。

※この記事を読んだ感想をいただけると、うれしいです。以下の「お問合わせ」フォームからお願いいたします。

お問い合わせ | note（ノート）

参考文献

改訂版 教科書傍用 スタンダード・オリジナル 数学III（数研出版、ISBN9784410209567）

演習問題

楕円

$$
\frac{x^2}{8}+\frac{y^2}{4}=1
$$

上の点$${(2,p)}$$を通り、この楕円の焦点を焦点とする双曲線の方程式を求めた上で、楕円を赤色、双曲線を青色、点$${(2,p)}$$を緑色で描くプログラムを作成してください。

演習問題の解答例