
高校数学をプログラミングで解く(コラム)「1-4 『情報』の試作問題「第2問」」
はじめに
この記事では、令和7年度の大学入学共通テスト(旧センター試験)で新たな受験科目となる『情報』について、独立行政法人大学入試センター(DNC)が出している『情報』の試作問題を扱います。
https://www.dnc.ac.jp/albums/abm.php?d=511&f=abm00003277.pdf&n=6-2-1_試作問題『情報Ⅰ』※令和4年12月23日一部修正.pdf
令和7年度以降に大学受験をされる方は、本記事をお読みになる前に、是非一度この試作問題を実際にやってみてください。
試作問題「第2問」
今回は、『情報』の試作問題の第2問について考えてみます。
「第2問」の概要
「第2問」はAとBの2つの問題で構成されており、配点としては各15点の計30点になります。
独立行政法人大学入試センター(DNC)の
「令和7年度試験の問題作成の方向性、試作問題等」( https://www.dnc.ac.jp/kyotsu/shiken_jouhou/r7/r7_kentoujoukyou/r7mondai.html )
のページに、『令和7年度大学入学共通テスト 試作問題「情報」の概要』(https://www.dnc.ac.jp/albums/abm.php?d=511&f=abm00003141.pdf&n=6-1_概要「情報」.pdf)という資料があります。この資料のp.6にこの第2問の概要がまとめられています(図1)。

第2問 A の概要
二次元コードに関する問題です。
スマートフォンなどで二次元コードを読み込んだことがある人は、二次元コードに何らかの文字情報を入れることができると、なんとなく理解することができると思いますが、二次元コードと文字情報とをどのようにして結び付けているのかはよくわからないですね。だから一見難しそうに感じますが、この問題も落ち着いて読んでみると、二次元コードについてはあまり知らなくても解くことができます。
第2問 A 問1
図1の「各設問の概要」にある通り、特許権に関する知識が必要になりますが、そんなに詳しく知っておく必要はなさそうです。特許が「ある発明をした人がその発明を独占的に使用できる権利」だということをなんとなく知っていれば、この権利を主張したらどうなるか、もなんとなくわかると思います。
第2問 A 問2
こちらも図2、図3を見ながら解答群の文を読んでみると、正しいことを書いているか、誤ったことを書いていることがわかってきます。ただし、画素や解像度についての知識を知っておく必要があります。
以下、選択肢ごとに見ていきます。
「① 円形では,(d)~(f)の角度によって黒白の比が異なってしまい,正しく読み取れなくなる可能性があるから。」
これは明らかにおかしいです。(d)~(f)のどの角度でも黒白の比は同じですね。そもそも問2の問題文に『下線部Aの目印は,図2のように,例えば(a)~(c)のどの角度で読み取っても,黒白黒白黒の比が 1:1:3:1:1 となることで,二次元コードの目印として認識できるようになっている。これは,図3のように円形の目印でも同じと考えられる』と書いてありますね。
「② 円形だと上下左右がないので,二次元コードの向きが分からなくなるから。」
『円形だと上下左右がない』というのはわかりますが、その理由で二次元コードの向きが分からなくなるというのはおかしいです。問題文中の『図1 二次元コードの例』(図2)を見てみると、二次元コードの向きを考えるポイントは二次元コードの目印として同じ形のものが左上、右上、左下の3か所にあることであって、その形状はある程度違っていても問題ないはずです。つまり、円形であっても左上、右上、左下の3か所にあれば二次元コードの向きはわかります。

「③ プリンタやディスプレイの解像度によっては,正方形の目印に比べて正しく読み取れる小さな円形の目印を作ることが難しくなるから。」
この問2の正解はこの③になります。
解像度とは何かについて説明しておきます。例えば、問題文中の図3をWindowsの「ペイント」を使って5倍に拡大してみてみると、以下の図3のようになります。

図3をよく見てみると、小さな正方形を並べることで円が描かれていることがわかると思います。この小さな正方形を画素と呼びます。解像度とは対象の図形がどのくらいの数の画素で構成されているかを示すものです。解像度が高いとたくさんの画素で図形を構成するため、画素が正方形であっても図3のように円のように見えます。一方、解像度が低い場合は、図形を構成する画素が少ないため、画素の正方形が目立ってしまい、円形とはいいがたくなってきます(図4)。そのため、『小さな円形の目印』の場合、『黒白黒白黒の比が 1:1:3:1:1』という情報は角度によって読み取りにくくなります。

なお、画素については、記事『高校数学をプログラミングで解く(準備編)「1-2 プログラムを書く」』でも解説していますので、そちらもご覧ください。
「④ 円形では目印が斜めに傾いていても,それを認識することができないため正しく読み取ることができないから。」
④は正しいか正しくないか、少し迷ってしまいます。確かに、目印が斜めに傾いていたら正しく読み取ることができなさそうです。ただ、これって円形だけでなく、正方形の場合も同じことが起こりそうです。つまり、形状に関係なく起こるということで、④は誤りとなります。
第2問 A 問3
この問3は二次元コードの問題ですが、二次元コードの知識はほぼ必要ないですね。問題文中の表1(図5)をみて、文字数や復元能力と二次元コードのサイズ(セルの数)との関係を読み取ることができれば、正しい解答ができます。

以下、選択肢ごとに見ていきます。
「⓪ 同じ復元能力であれば,文字数に比例してセルの数が多くなり,同じセルの大きさであれば二次元コードも大きくなる。」
これは違いますね。
文字数が増えると二次元コードも大きくなりますが、比例はしていないですね。例えば、復元能力7%の場合、20文字と30文字の場合の2次元コードを比較すると、同じサイズ(セルの数)になっています。
「① 復元能力ごとに,文字数の一定の範囲でセルの縦と横の数が決まり,文字数が多くなるほど段階的にセルの縦と横の数は多くなる。」
これは正しいです。
復元能力7%の場合の20文字と30文字の2次元コードが同じサイズ(セルの数)になっていることなどから「文字数の一定の範囲でセルの縦と横の数が決まり」が読み取れますし、復元能力7%も復元能力30%も文字数が増えていくにつれて、段階的にセルの縦と横の数は多くなっています。
「② 文字数とセルの数には関係が見られない。」
これは明らかに違います。
「③ ある文字列を復元能力30%で作成した二次元コードは,同じ文字列を復元能力7%で作成したものに比べ約4倍のセルの数がある。」
これも正しくないです。
約4倍となると、縦に並んだセルの数と横に並んだセルの数がそれぞれ約2倍になることになりますが、そのようにはなっていないですね。
「④ 復元能力30%にするためには,復元能力7%と比べより多くの情報が必要となる。」
これは正しいです。
表を縦に見ていくと、それぞれの文字数に対して復元能力が高くなると、二次元コードのセルの数がいずれも増えているのがわかります。これは、より多くの情報を入れることができるようにするためと考えることができます。
「⑤ 同じ文字数であれば復元能力を変えてもセルの数は変わらない。」
これも明らかに間違いです。
第2問 A 問4
この問4も、二次元コードの知識はほぼ必要ないです。問題文中の表1(図5)をみて、文字数を増やしたり復元能力をあげたりすると、二次元コードのサイズ(セルの数)が大きくなることを理解しておけばおのずとわかってきます。
第2問 B の概要
模擬店の待ち行列に関する問題です。
客を待たせないようにするために、1日目の待ち状況を分析してシミュレーションを行い、改善策を考えようというもの。
この問題は、「相対度数」や「累積相対度数」などの聞きなれない用語がでてきますが、問題文を読んで各表をよく見てみることでなんとか理解できると思います。特に、各表を見て何を表しているのかを考え、時折類推しながら解いていくことになります。
第2問 B 問1
まず、1つ目の問い「ケ」の部分を考えてみます。これを行うために問題文中の表1(図6)と問題文中の表2(図7)を見比べて、表2の到着間隔を算出するルールを導いてみます。


例えば、表2の「2人目」のデータを見てみると、生成させた乱数が0.31、到着間隔が2分となっています。なぜ、このような結果になったのかを考えます。
表1の累積相対度数の値をみると、生成させた乱数の値0.31は、0.26と0.42との間にあります。そして、0.26は階級値1分に対する累積相対度数で、0.42は階級値2分に対する累積相対度数です。このことから「生成させた乱数の値が階級値1分に対する累積相対度数と階級値2分に対する累積相対度数との間にある場合、表2の到着間隔は2分となる」と類推できます。つまり、「生成させた乱数の値が階級値$${n-1}$$分に対する累積相対度数と階級値$${n}$$分に対する累積相対度数との間にある場合、表2の到着間隔は$${n}$$分となる」と推測します。
この推測が正しいかどうか判断するために、表2の「3人目」のデータを見てみます。生成させた乱数の値は0.66となっています。これは、表1の累積相対度数の値でみると、0.64と0.82との間にありますので、推測したルールに従うと、到着間隔は4分になるはずです。表2をみるとそのようになっているので、このルールは正しそうです。
では、このルールで問題の「10人目」を見てみましょう。生成させた乱数の値は0.95になっております。これは表1の累積相対度数の値でみると、0.94と0.96との間にあります。このことから推測したルールに従うと、到着間隔は8分となります。つまり、「ケ」は 8 となります。
続いて、「コ」「サ」「シ」の部分です。
これらを考えるために、問題文中の図1が途中まで作成されているので、これを完成させます(図8)。
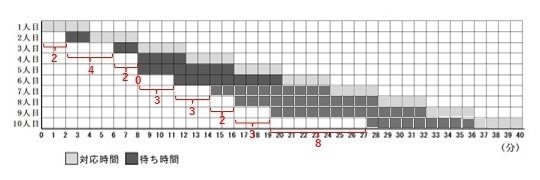
ポイントは、対応時間(薄いグレーの部分)は4分おきに階段状に描かれること、そして表2の到着間隔(図8に赤色で表示)に依存して客の待ち時間が始まるということです。これにより、客の待ち時間(濃いグレーの部分)が決まります。
この図8を見ると、最も待ち人数が多いときは19分から20分までの間で4名(これが「コ」の答え)となり、また、客の中で最も待ち時間が長いのは9人目の客で濃いグレーの矩形の数を数えて、13分(これが「サ」「シ」の答え)となります。
第2問 B 問2
この問題は問題文中の図2(図9)をきちんと分析することができれば、そんなに難しくないです。仮に、問1が解けなくても解答可能だと思います。

以下、選択肢ごとに見ていきます。
「⓪ 来客人数が多くなるほど,最大待ち人数が多くなる傾向がある。」
これは、来客人数が増えるにつれて、グラフは右に拡がっていっていますので、最大待ち人数が多くなる傾向にあるといえ、問題文中の図2から読み取ることができます。
「① 最大待ち人数の分布は,来客人数の半数以下に収まっている。」
これは、来客人数10人の場合のグラフを見ると、最大待ち人数が6人の場合があり、来客人数の半数(5人)より多くなっているため、これは読み取ることができません。したがって、この問題の正解は①になります。
「② 最大待ち人数は,来客人数の 1/4 前後の人数の頻度が高くなっている。」
各グラフは、来客人数10人の場合3人、来客人数20人の場合5人、来客人数30人の場合8人、来客人数40人の場合10人で頻度のピークがみられます。つまり、来客人数の 1/4 前後の人数の頻度が高くなっており、これは読み取ることができます。
「③ 来客人数が多くなるほど,最大待ち人数の散らばりが大きくなっている。」
これは、来客人数が増えるにつれて、グラフは拡がっていっていますので、最大待ち人数の散らばりが大きくなっているといえます。したがって、これも読み取ることができます。
第2問 B 問3
この問題は一人の客への対応時間を 4 分から 3 分に短縮できたら確実に待ち時間は減るだろうことを考えると、最大待ち人数は全体的に少なくなるでしょう。そう考えると、最大待ち人数のピーク位置が下がっている(左に移動している)⓪のグラフのような形になると考えることができます。
まとめ
今回は、令和7年度の大学入学共通テスト(旧センター試験)で新たな受験科目となる『情報』について、独立行政法人大学入試センター(DNC)が出している『情報』の試作問題の第2問を考えてみました。
第2問は、大きくAとBの2つの問題に分かれており、Aの問題は二次元コードに関する問題、Bの問題は待ち状況改善のためのシミュレーションに関する問題になっています。
Aの問題は二次元コードということで一見難しそうですが、実際に問題を解いてみると二次元コードの知識はほとんど必要ないことがわかります。
Bの問題は、相対度数や累積相対度数などあまり聞きなれない用語が出てきます。そのため問1は少しとっつきずらいかもしれませんが、問題文を読んで表や図をしっかり見ながら分析していくと理解することができます。一度は根気強くやっておきましょう。ただ、問2, 問3については問1に比べて結構簡単になっています。受験のときは、問1のような問題は後回しにして、問2、問3のような問題から解答しておく方がよいでしょう。
参考文献
独立行政法人大学入試センター(DNC)のWebサイト
「令和7年度試験の問題作成の方向性、試作問題等」https://www.dnc.ac.jp/kyotsu/shiken_jouhou/r7/r7_kentoujoukyou/r7mondai.html
高等学校『情報I』数研出版、ISBN:9784410821219
この記事が気に入ったらサポートをしてみませんか?
