高校数学をプログラミングで解く（数学II編）「5-5 方程式の実数解」

マガジンリスト　＞　数学Ⅱ編 5.微分法と積分法　＞　5-5 方程式の実数解

はじめに

今回は、数学IIで学ぶ「方程式の実数解」について、特に３次方程式に対する異なる実数解の個数を求める問題を解き、その結果をグラフで再現するプログラムを作成します。

方程式の実数解

まず、方程式の実数解について解説しておきます。

方程式の実数解

① $${f(x)=0}$$の実数解は、曲線$${y=f(x)}$$と$${x}$$軸の共有点の$${x}$$座標である。
② $${f(x)=g(x)}$$の実数解は、２つの曲線$${y=f(x), y=g(x)}$$の共有点の$${x}$$座標である。
③ $${f(x)}$$が$${x}$$の整式で表された関数で$${a < b}$$のとき、
$${f(a)f(b)<0}$$ $${ \Rightarrow }$$ $${f(x)=0}$$は$${a < x < b}$$に少なくとも１つの実数解をもつ。ただし、逆は成り立たない。

方程式の実数解の個数を求める

今回は、方程式の実数解の個数を求めておいて、それをグラフとして再現するプログラムを作成してみます。

問題
$${a}$$は定数とする。$${2x^3+9x^2-3-a=0}$$の異なる実数解の個数を調べよ。

問題の解答

方程式を変形すると、

$$
2x^3+9x^2-3 = a
$$

となります。方程式の実数解は、曲線

$$
y=2x^3+9x^2-3
$$

と、直線

$$
y=a
$$

の共有点の$${x}$$座標で表されます。曲線において

$$
y' = 6x^2+18x = 6x(x+3)
$$

となるので、曲線は、$${x=-3}$$で極大値$${y=24}$$、$${x=0}$$で極小値$${y=-3}$$を持つことがわかります。したがって、$${2x^3+9x^2-3-a=0}$$の異なる実数解は、
i) $${a>24}$$のとき、１つの実数解をもつ。
ii) $${a=24}$$のとき、２つの異なる実数解をもつ。
iii) $${-3 < a < 24}$$のとき、３つの異なる実数解をもつ。
iv) $${a = -3}$$のとき、２つの異なる実数解をもつ。
v) $${a < -3}$$のとき、１つの実数解をもつ。
となります。

プログラム

今回のプログラムはこれまでと趣向が違いますので、注意してください。つまり、問題の答えを求めるためのプログラムではなく、上記の解答をもとに解答をグラフで再現するプログラムといった方がわかりやすいでしょう。

記事『高校数学をプログラミングで解く（数学II編）「5-3 関数の値の変化」』で作成したスケッチ「calcandplotExtrema」を再利用して作成していきます。
スケッチ「calcandplotExtrema」をフォルダごとコピーして、スケッチの名前（フォルダ名）を「numberofRealRoots」と変更し、またスケッチ「numberofRealRoots」内の「calcandplotExtrema.pde」ファイルの名前を「numberofRealRoots.pde」に変更します。そして、pdeファイル「numberofRealRoots.pde」をダブルクリックしてスケッチ「numberofRealRoots」の開発環境ウィンドウを立ち上げます。開発環境ウィンドウのタブ欄で「numberofRealRoots」タブを選択し、そのテキストエリアのソースコードを以下で書き換えます。

float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 50.0; // y軸の表示範囲 -y_rangeからy_rangeまで 

float local_maximum; // 極大値
float local_minimum; // 極小値
float local_maximum_pos; // 極大値の位置
float local_minimum_pos; // 極小値の位置

// ３次関数の係数
float a = 2.0;  // x^3の係数
float b = 9.0;  // x^2の係数
float c = 0.0;  // xの係数
float d = -3.0;  // 定数項

// x軸と平行な直線の切片
float A = -y_range;

void setup(){
  size(500,500);
  background(204,204,204);  
  noFill();

  // 日本語のフォントを設定
  PFont font = createFont("Meiryo", 12);
  textFont(font);
  
  // 極値を計算する
  calc_extrema(a,b,c,d);

}

void draw(){
  background(204,204,204);
  if(mousePressed){
    A = 2.0 * y_range / height * ( height / 2.0 - mouseY );
  }
  
  if( A > local_maximum ){
    text("a="+A+"のとき、異なる実数解は1つ", 0,0);
  } else if( A == local_maximum ){
    text("a="+A+"のとき、異なる実数解は2つ", 0,0);
  } else if( A < local_maximum && A > local_minimum){
    text("a="+A+"のとき、異なる実数解は3つ", 0,0);
  } else if(  A == local_minimum){
    text("a="+A+"のとき、異なる実数解は2つ", 0,0);
  } else {
    text("a="+A+"のとき、異なる実数解は1つ", 0,0);
  } 
  
  setAxes(x_range, y_range); // 座標軸の準備
  
  // ３次関数を描画  
  draw_cubic_function(a,b,c,d,-x_range, x_range);
  // 極値をプロットする
  stroke(255,0,0);
  plot_extrema_point(a,b,c,d,local_maximum_pos);
  stroke(0,0,255);
  plot_extrema_point(a,b,c,d,local_minimum_pos);
  // x軸と平行な直線を描画
  stroke(0,0,0);
  draw_line(A);

}  

// ３次関数
float f(
  float a, // x^3の係数
  float b, // x^2の係数
  float c, // xの係数
  float d, // 定数項
  float x 
){
  return a*x*x*x + b*x*x + c*x + d;
}

// ３次関数の導関数
float f_prime(
  float a, // x^3の係数
  float b, // x^2の係数
  float c, // xの係数
  float x
){
  return 3.0*a*x*x + 2.0*b*x + c;
}

// ３次関数を描く関数
void draw_cubic_function(
  float a, // x^3の係数
  float b, // x^2の係数
  float c, // xの係数  
  float d,  // 定数項
  float x_min, // グラフの定義域の下限
  float x_max  // グラフの定義域の上限
){
  int plot_num = 2000; // グラフを描くための頂点の個数  
  // グラフを描画
  float x, y; // 関数の座標
  float X, Y; // キャンバス上の座標 
  beginShape();
  for(int i=1; i<plot_num; i++){
    x = x_min + (x_max - x_min) / plot_num * i; // 曲線上の点のx座標
    y = f(a,b,c,d,x); // 曲線上の点のyの値
    // キャンバス上の座標位置に換算
    X = width / 2.0 / x_range * x;
    Y = height / 2.0 / y_range * y;
    vertex(X, Y);
  }
  endShape();

}

// 極値を計算する関数
void calc_extrema(
  float a, // x^3の係数
  float b, // x^2の係数
  float c, // xの係数  
  float d  // 定数項
){
  // 極値前後の小さな区間[x-e,x+e]
  float e = 0.01;
  // f'(x)=0（２次方程式）の判別式を計算する
  float D = (2.0*b)*(2.0*b)-4.0*(3.0*a)*c;
  if( D > 0.0 ){ // 2つの極値をもつとき
    // 1つ目の極値
    float x1 = (-(2.0*b)-sqrt(D))/2.0/(3.0*a);
    float y1 = f(a,b,c,d,x1);
    float before_x1 = f_prime(a,b,c,x1-e);
    float after_x1 = f_prime(a,b,c,x1+e);
    if( before_x1 > 0.0 && after_x1 < 0.0 ){
      // 極大値であれば赤色でプロット
      stroke(255,0,0);
      local_maximum_pos = x1;      
      local_maximum = y1;
      println("極大値:", x1, y1);
    } else if(before_x1 < 0.0 && after_x1 > 0.0 ){
      // 極小値であれば青色でプロット
      stroke(0,0,255);
      local_minimum_pos = x1;
      local_minimum = y1;
      println("極小値:", x1, y1);
    } else {
      // 極値でなければ緑色でプロット
      stroke(0,255,0);
      println("極値ではない:", x1, y1);
    }
    plot_extrema_point(a,b,c,d,x1);
    
    // 2つ目の極値
    float x2 = (-(2.0*b)+sqrt(D))/2.0/(3.0*a);
    float y2 = f(a,b,c,d,x2);
    float before_x2 = f_prime(a,b,c,x2-e);
    float after_x2 = f_prime(a,b,c,x2+e);
    if( before_x2 > 0.0 && after_x2 < 0.0 ){
      // 極大値であれば赤色でプロット
      stroke(255,0,0);
      local_maximum_pos = x2;
      local_maximum = y2;
      println("極大値:", x2, y2);
    } else if(before_x2 < 0.0 && after_x2 > 0.0 ){
      // 極小値であれば青色でプロット
      stroke(0,0,255);
      local_minimum_pos = x2;
      local_minimum = y2;
      println("極小値:", x2, y2);
    } else {
      // 極値でなければ緑色でプロット
      stroke(0,255,0);
      println("極値ではない:", x2, y2);
    }
    plot_extrema_point(a,b,c,d,x2);
    
  } else { // D ≦ 0　の場合
    println("極値なし");
  }
  
}

// 極値をプロットする関数
void plot_extrema_point(
  float a, // x^3の係数
  float b, // x^2の係数
  float c, // xの係数  
  float d, // 定数項
  float x // 極値のx座標
){
  float y = f(a,b,c,d,x);
  float X, Y; // キャンバス上の座標
  // キャンバス上の座標位置に換算
  X = width / 2.0 / x_range * x;
  Y = height / 2.0 / y_range * y;
  strokeWeight(5);
  point(X, Y);
  strokeWeight(1);
}

// x軸と平行な直線を描く関数
void draw_line(
  float A 
){
  float Y; // キャンバス上の座標
  // キャンバス上の座標位置に換算
  Y = height / 2.0 / y_range * A;
  line(-width/2, Y, width/2, Y);

}

ソースコード1　解答をグラフで再現するプログラム

ソースコード1を、スケッチ「numberofRealRoots」の「numberofRealRoots」タブのテキストエディタ部分に書いて実行すると、図1のように、実行ウィンドウのキャンバス上に関数$${y=2x^3+9x^2-3}$$のグラフとその関数の極大値（赤色）、極小値（青色）が描かれます。

図1　グラフと極値

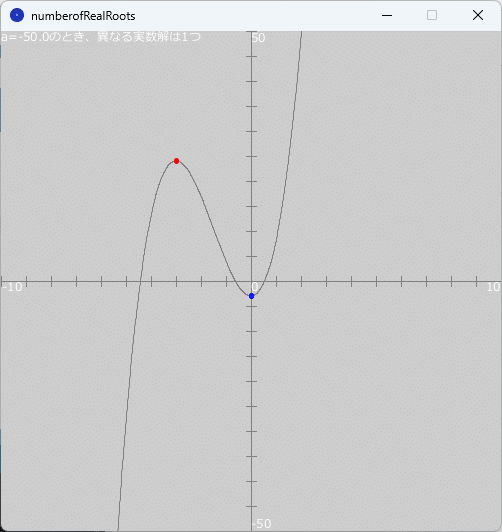
この実行ウィンドウのキャンバス上の適当な箇所をクリックすると、その位置の高さに直線$${y=a}$$が描かれます。そして、キャンバスの左上の位置にそのときの$${a}$$の値と方程式関数$${2x^3+9x^2-3=a}$$の異なる実数解の個数が表示されます（図2参照）。

図2　キャンバス上をクリックしたとき

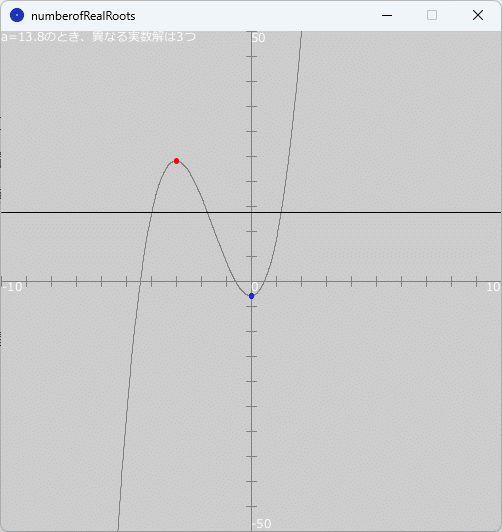
プログラムの解説

今回のプログラム（ソースコード1）は、記事『高校数学をプログラミングで解く（数学II編）「5-3 関数の値の変化」』で作成したスケッチ「calcandplotExtrema」を加筆・修正して作成しています。このあたりを簡単に説明します。

極値を計算してプロットする関数について
スケッチ「calcandplotExtrema」では、calc_and_plot_extrema 関数を用意し、極値の計算とその極値をグラフにプロットすることを一つの関数で行っていましたが、今回は、極値を計算する関数 calc_extrema と極値をグラフにプロットする関数 plot_extrema_point に分けました。

変数を setup 関数の外で宣言、初期化
スケッチ「calcandplotExtrema」では、３次関数の係数などを setup 関数内で宣言や初期化を行っていましたが、今回は、setup 関数と draw 関数の両方で利用するため、共通で利用する変数はプログラムの上部、setup 関数や draw 関数の外で宣言や初期化を行っています。

float x_range = 10.0; // x軸の表示範囲 -x_rangeからx_rangeまで
float y_range = 50.0; // y軸の表示範囲 -y_rangeからy_rangeまで 

float local_maximum; // 極大値
float local_minimum; // 極小値
float local_maximum_pos; // 極大値の位置
float local_minimum_pos; // 極小値の位置

// ３次関数の係数
float a = 2.0;  // x^3の係数
float b = 9.0;  // x^2の係数
float c = 0.0;  // xの係数
float d = -3.0;  // 定数項

// x軸と平行な直線の切片
float A = -y_range;

setup 関数内で行うこと
今回のプログラムの setup 関数内で行うことは、極値の計算です。極値は一度計算しておけばよいので、setup 関数内で計算しておきます。

draw 関数内で行うこと
今回のプログラムでは、キャンバス上の適当な箇所をクリックすると、その位置の高さに直線$${y=a}$$が描かれるようにします。そのため、グラフなどの描画部分は draw 関数内で行います。draw関数内での処理の流れについてまとめておきます。
① background 関数を呼び出し、キャンバス上をグレーで塗りつぶします。
② キャンバス上の適当な箇所がクリックされたら、クリックされた箇所の$${y}$$成分の値をもとに、$${x}$$軸に平行な直線の位置（切片）を表す変数 A を更新します。クリックされなければ、そのまま③の処理に進みます。
③ 変数 A の値に応じて、方程式の異なる実数解の個数をキャンバスの左上に表示します。
④ 最後に、３次関数の描画、極値のプロット、$${x}$$軸に平行な直線の描画を行います。

まとめ

今回は、数学IIで学ぶ「方程式の実数解」について、特に３次方程式に対する異なる実数解の個数を求める問題を解き、その結果をグラフで再現するプログラムを作成しました。
今回は、キャンバス上の適当な箇所をクリックすると、その位置の高さに直線$${y=a}$$が描かれるようにしました。これを行うために、 draw 関数を導入して、クリックをされたら更新が行えるようにしました。このあたりについて今回はあまり詳しく説明しませんが、ソースコード1を丁寧にチェックしつつ、わからない箇所はネットで確認してみると、少しずつ理解が深まるでしょう。こういう経験がプログラミングの力を伸ばしていきますので、是非考えてみてください。

参考文献

改訂版 教科書傍用 スタンダード 数学II（数研出版、ISBN9784410209369）

Processingをはじめよう 第２版（オライリー・ジャパン、ISBN9784873117737）